| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tuv0k
Forumaš(ica)
Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)
Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)
Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
 Postano: 17:50 sri, 2. 7. 2008 Naslov: |
    |
|
|
@Luuka - u njegovom slucaju stvar ide od 2, tj. 2^1, a ne od 1, tj. 2^0 sto trazi 'velika zagrada' :)
[quote="tuv0k"]E sada, to sam zapisao kao [latex]2+2^2+2^3+ ... +2^n[/latex]= ??
znam da mi je [latex]n=40183[/latex], ali ne znam kako to izračunati...[/quote]
pa upravo primjenivsi formulu koju su ti dali :)
[latex]2 + 2^2 + 2^3 + \ldots + 2^n = 2^1 + 2^2 + 2^3 + \ldots + 2^n = 2 (2^0 + 2^1 + 2^2 + 2^3 + \ldots + 2^{n-1}) = 2 (1 + 2^1 + 2^2 + 2^3 + \ldots + 2^{n-1}) = 2 (2^{n-1} - 1) = 2^{n+1}-2 [/latex]
prije ovog pretposljednjeg jednako imas 2 * velika zagrada koja ide do 2^{n-1} :)
tj. u tvom konkretnom primjeru rjesenje ti je
[latex]2 (2^{40182}-1) = 2^{40183} - 2[/latex]
a onda zakljucis da je to dovoljno, a neka si to pretvara u mnogoznamenkasti broj onaj kome treba :)
ili [bg=yellow]krace[/bg] - tvoj izraz je skoro kao [latex]2^{n+1}[/latex] (za 2^n izraz treba ici do n-1, a tebi ide do n, dakle, to je 2^{n+1})
e onda, ti pocinjes sa 2, a ne sa 1, znaci, to treba oduzeti ...
dakle
[latex]1 + tvoje = 2^{n+1} - 1 \Rightarrow tvoje = 2^{n+1} - 2[/latex]
@Luuka - u njegovom slucaju stvar ide od 2, tj. 2^1, a ne od 1, tj. 2^0 sto trazi 'velika zagrada' 
| tuv0k (napisa): | E sada, to sam zapisao kao  = ??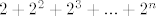
znam da mi je 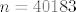 , ali ne znam kako to izračunati... |
pa upravo primjenivsi formulu koju su ti dali
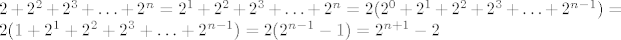
prije ovog pretposljednjeg jednako imas 2 * velika zagrada koja ide do 2^{n-1}
tj. u tvom konkretnom primjeru rjesenje ti je
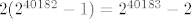
a onda zakljucis da je to dovoljno, a neka si to pretvara u mnogoznamenkasti broj onaj kome treba
ili krace - tvoj izraz je skoro kao 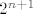 (za 2^n izraz treba ici do n-1, a tebi ide do n, dakle, to je 2^{n+1})
e onda, ti pocinjes sa 2, a ne sa 1, znaci, to treba oduzeti ...
dakle
|
|
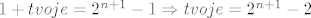
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol:
Lokacija: /sbin/init
|
| Postano: 17:52 sri, 2. 7. 2008 Naslov: |
|
|
|
Da skratimo, ona velika zagrada je
[latex]2^{40183+1}-1[/latex],
cemu jos treba oduzeti 1 (jer krecemo od 2, a ne od 1) da bismo dobili sumu s pocetka ove prepiske. :) Dakle, rezultat bi bio:
[latex]2^{40184}-2[/latex]. 8)
kome se to raspisuje... sretno! ;) Recimo, Mathematica bi to trebala znati lijepo rijesiti, mada ja ne vidim neku korist od broja koji bi trebao imati oko 1200 znamenaka. :lol:
Da skratimo, ona velika zagrada je
 ,
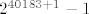cemu jos treba oduzeti 1 (jer krecemo od 2, a ne od 1) da bismo dobili sumu s pocetka ove prepiske. Dakle, rezultat bi bio:
 . 
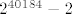kome se to raspisuje... sretno!  Recimo, Mathematica bi to trebala znati lijepo rijesiti, mada ja ne vidim neku korist od broja koji bi trebao imati oko 1200 znamenaka. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
goranm
Forumaš(ica)
Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol:
|
|
| [Vrh] |
|
ma
Forumaš(ica)
Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol:
|
| Postano: 20:59 sri, 2. 7. 2008 Naslov: |
|
|
|
[quote="goranm"]A kako to da u 100 godina ima 40183 dana? Trebalo bi biti između 36500 (100 neprijestupnih godina) i 36600 (100 prijestupnih godina) dana. Recimo da brojimo od 2008. do 2108.
Imamo barem 100*365=36500 dana. Svaka 4. godina uključujući 2008. dolazi 26 puta pa pridodajemo još 26 dana. Godina 2100. upada u "svake 4. godine od 2008." i djeljiva je sa 100 pa nije prijestupna. Oduzimamo jedan dan. Dakle, u 100 godina ima 36525 dana. :)[/quote]
ali ako je 2008. jedna od tih 100 godina, onda 2108. nije (to je već 101.), pa zapravo imamo 36524 dana.
usput, ako je broj godine djeljiv s 400, tada ona ipak [b]jest[/b] prijestupna, pa bismo, primjerice, u razdoblju od 1. siječnja 2000. do 31. prosinca 2099. imali 36525 dana. :wink:
| goranm (napisa): | A kako to da u 100 godina ima 40183 dana? Trebalo bi biti između 36500 (100 neprijestupnih godina) i 36600 (100 prijestupnih godina) dana. Recimo da brojimo od 2008. do 2108.
Imamo barem 100*365=36500 dana. Svaka 4. godina uključujući 2008. dolazi 26 puta pa pridodajemo još 26 dana. Godina 2100. upada u "svake 4. godine od 2008." i djeljiva je sa 100 pa nije prijestupna. Oduzimamo jedan dan. Dakle, u 100 godina ima 36525 dana. |
ali ako je 2008. jedna od tih 100 godina, onda 2108. nije (to je već 101.), pa zapravo imamo 36524 dana.
usput, ako je broj godine djeljiv s 400, tada ona ipak jest prijestupna, pa bismo, primjerice, u razdoblju od 1. siječnja 2000. do 31. prosinca 2099. imali 36525 dana.
_________________
ima let u finish
|
|
| [Vrh] |
|
goranm
Forumaš(ica)
Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol:
|
| Postano: 21:05 sri, 2. 7. 2008 Naslov: |
|
|
|
[quote="ma"]ali ako je 2008. jedna od tih 100 godina, onda 2108. nije (to je već 101.), pa zapravo imamo 36524 dana.[/quote]
U
P
S
:lol: :D
[quote]usput, ako je broj godine djeljiv s 400, tada ona ipak [b]jest[/b] prijestupna, pa bismo, primjerice, u razdoblju od 1. siječnja 2000. do 31. prosinca 2099. imali 36525 dana. :wink:[/quote]
Jedna čudna stvar je da godina 4000. možda neće biti prijestupna iako je djeljiva sa 400 kako bi se nadoknadio zaostatak od jednog dana koji kalendar napravi svakih 8000 godina :lol:
| ma (napisa): | | ali ako je 2008. jedna od tih 100 godina, onda 2108. nije (to je već 101.), pa zapravo imamo 36524 dana. |
U
P
S
| Citat: | | usput, ako je broj godine djeljiv s 400, tada ona ipak jest prijestupna, pa bismo, primjerice, u razdoblju od 1. siječnja 2000. do 31. prosinca 2099. imali 36525 dana. |
Jedna čudna stvar je da godina 4000. možda neće biti prijestupna iako je djeljiva sa 400 kako bi se nadoknadio zaostatak od jednog dana koji kalendar napravi svakih 8000 godina
_________________
The Dude Abides
|
|
| [Vrh] |
|
ma
Forumaš(ica)
Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol:
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)
Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol:
Lokacija: Void
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3560)16
Spol:
Lokacija: /sbin/init
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo
Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)
Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)
Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
| Postano: 9:52 ned, 6. 7. 2008 Naslov: |
|
|
|
našao sam jedan zadatak...pa me zanima jesam li ga točno riješio pošto nemam uvid u rješenje...
Posljednji 25-ti red stadiona može primiti 2048 gledatelja. Svaki prethodni red prima 20 gledatelja manje.
a)Koliko gledatelja prima prvi red stadiona?
b)Koliko je gledatelja na stadionu ako je on popunjen do posljednjeg mjesta?
c)Svečana loža stadiona ima 225 mjesta i smještena je unutar 5-og i 10-og reda. Svaki njezi red počevši od najnižeg ima 5 redova više nego prethodni. Koliko ima mjesta u prvom redu lože?
a)[latex]y=broj gledatelja[/latex]
[latex]x=broj redova[/latex]
[latex]y=2068-20x[/latex]
pošto stadion ima 25 redova, točnija formula bi bila [latex]y=1548+20x[/latex]
Odgovor bi bio da prvi red stadiona prima 1568 gledatelja
b)Dakle po meni treba odrediti sumu [latex]1588+1608+1628+...+2048=???[/latex]
[latex]a + (a+20) + (a+40)+...+(a+480)=???[/latex]
pošto je broj redova 25, imamo [latex]25a[/latex]
treba odrediti sumu [latex]20+40+60+...+480[/latex]
ukupno imamo [latex]480/20=24 broja [/latex], što znači 12 parova
[latex]12*500=6000[/latex]
pa bi formula glasila [latex]25a+6000[/latex]
U našem slučaju [latex]a=1568, 25*1568+6000=45200[/latex]
c)imamo 225 mjesta, i 5 redova. U svakom redu je 5 više što znači da je ukupna razlika prvog i posljednjeg reda 25.
dakle:
[latex]x+(x+5)+(x+10)+...+(x+25)=225
6x+75=225
x=25[/latex]
što na govori da je u posljednjem redu svečane lože 25 gledatelja...
a u prvom je [latex]25+30+35+40+45+50, 50 gledatelja[/latex]
EDIT:Zeza me latex :D
našao sam jedan zadatak...pa me zanima jesam li ga točno riješio pošto nemam uvid u rješenje...
Posljednji 25-ti red stadiona može primiti 2048 gledatelja. Svaki prethodni red prima 20 gledatelja manje.
a)Koliko gledatelja prima prvi red stadiona?
b)Koliko je gledatelja na stadionu ako je on popunjen do posljednjeg mjesta?
c)Svečana loža stadiona ima 225 mjesta i smještena je unutar 5-og i 10-og reda. Svaki njezi red počevši od najnižeg ima 5 redova više nego prethodni. Koliko ima mjesta u prvom redu lože?
a)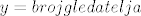
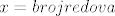
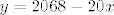
pošto stadion ima 25 redova, točnija formula bi bila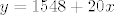 
Odgovor bi bio da prvi red stadiona prima 1568 gledatelja
b)Dakle po meni treba odrediti sumu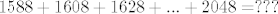 
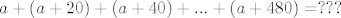
pošto je broj redova 25, imamo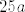 
treba odrediti sumu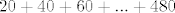 
ukupno imamo 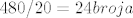 , što znači 12 parova
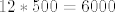
pa bi formula glasila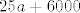 
U našem slučaju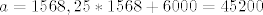 
c)imamo 225 mjesta, i 5 redova. U svakom redu je 5 više što znači da je ukupna razlika prvog i posljednjeg reda 25.
dakle:
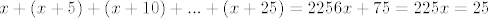
što na govori da je u posljednjem redu svečane lože 25 gledatelja...
a u prvom je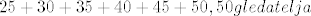 
EDIT:Zeza me latex
_________________
Čovjek koji ne mijenja mišljenje voli sebe više nego istinu!
Pomoću logike dokazujemo, ali pomoću intuicije otkrivamo!
Zadnja promjena: tuv0k; 10:16 ned, 6. 7. 2008; ukupno mijenjano 4 put/a.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
| Postano: 10:03 ned, 6. 7. 2008 Naslov: |
|
|
|
Hm... ja sam to ovak zamislio...
Neka nam je yi broj gledatelja u i-tom retku.
Sad vrijedi
yi=2048-(25-i)*20 , tj.
yi=1548+20i.
Sad je odgovor na prvo pitanje
y1 = 1548+20 = 1568.
Broj gledatelja je suma svih yi, za i=1,2,...,25.
Pa imamo:
[latex]\sum_{i=1}^{25}{y_i}=\sum_{i=1}^{25}{(1548+20i)}=1548 \cdot 25+20 \cdot \sum_{i=1}^{25}{i}=38700+20 \cdot 325=45200[/latex]
edit: aha, ima i svečana loža...
Dakle:
x+(x+5)+(x+10)+(x+15)+(x+20)=225 -> x=35.
:D
Hm... ja sam to ovak zamislio...
Neka nam je yi broj gledatelja u i-tom retku.
Sad vrijedi
yi=2048-(25-i)*20 , tj.
yi=1548+20i.
Sad je odgovor na prvo pitanje
y1 = 1548+20 = 1568.
Broj gledatelja je suma svih yi, za i=1,2,...,25.
Pa imamo:
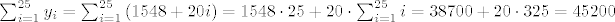
edit: aha, ima i svečana loža...
Dakle:
x+(x+5)+(x+10)+(x+15)+(x+20)=225 → x=35.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy
Zadnja promjena: Luuka; 10:22 ned, 6. 7. 2008; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)
Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
| Postano: 10:21 ned, 6. 7. 2008 Naslov: |
|
|
|
To je najgore kod takvih zadataka. Ne znaš dal je <5,10> ili [5,10> ili <5,10] ili [5,10]. Svakak se može shvatit. Al princip ti je dobar (i moj) a sad, koje je rješenje... :wink:
To je najgore kod takvih zadataka. Ne znaš dal je <5,10> ili [5,10> ili <5,10] ili [5,10]. Svakak se može shvatit. Al princip ti je dobar (i moj) a sad, koje je rješenje...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy |
|
| [Vrh] |
|
tuv0k
Forumaš(ica)
Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
|
