| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
 Postano: 10:30 pon, 7. 7. 2008 Naslov: Postano: 10:30 pon, 7. 7. 2008 Naslov: |
    |
|
|
Neka od pitanja s pismenog danas: (sistem je bio sličan kao [url=http://degiorgi.math.hr/forum/viewtopic.php?p=94880#94880]u prvom semestru[/url], dakle prvo su bile točno-netočno "pitalice" (treba skupiti [b]minimalno 5 bodova[/b], maksimalno je oko 20 (ne znam točno jer nisam brojala))
[b]Prvi dio:[/b]
1.) Ako su vektori x-y i x+y (realni unitarni prostor) međusobno okomiti, onda su nužno x i y jednake duljine.
2.) Ako za operator/matricu A vrijedi A^2 - A = 0, onda je im(A) + ker(A) = V.
3.) x [latex]\mapsto[/latex] 2x + i je linearno na C.
4.) Spektar matrice ostaje nepromijenjen ako matrici oduzmemo alfa*I.
5.) S={a[1], ..., a[r]} i G€M[rxr](R), s elementima g[ij] := <a[i] | a[j]>. S je linearno ovisan ako i samo ako je det G = 0.
6.) Matrice [latex]$$ \left[
\begin{array}{ c c c }
1 & 2 & 3 \\
2 & 3 & 4 \\
4 & 5 & 6
\end{array} \right]
$$[/latex] i [latex]$$ \left[
\begin{array}{ c c c }
2 & 1 & 1 \\
3 & 0 & 1 \\
4 & 2 & 1
\end{array} \right]
$$[/latex] su slične.
7.) Koji od navedenih operatora u kompleksnom prostoru su dijagonalizabilni: normalni, invertibilni, unitarni, ortogonalne projekcije.
8.) Što za operatore A i B [u]NE[/u] vrijedi na kompleksnom prostoru: (a+B)* = B* + A*, ((lambda)A)* = lambda(A*), (AB)* = A*B*, (A*)* = A.
Napišem i drugi dio mrvu kasnije, sad mi se žuri. :wink:
Neka od pitanja s pismenog danas: (sistem je bio sličan kao u prvom semestru, dakle prvo su bile točno-netočno "pitalice" (treba skupiti minimalno 5 bodova, maksimalno je oko 20 (ne znam točno jer nisam brojala))
Prvi dio:
1.) Ako su vektori x-y i x+y (realni unitarni prostor) međusobno okomiti, onda su nužno x i y jednake duljine.
2.) Ako za operator/matricu A vrijedi A^2 - A = 0, onda je im(A) + ker(A) = V.
3.) x  2x + i je linearno na C. 2x + i je linearno na C.
4.) Spektar matrice ostaje nepromijenjen ako matrici oduzmemo alfa*I.
5.) S={a[1], ..., a[r]} i G€M[rxr](R), s elementima g[ij] := <a[i] | a[j]>. S je linearno ovisan ako i samo ako je det G = 0.
6.) Matrice 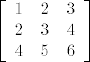 i i 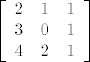 su slične. su slične.
7.) Koji od navedenih operatora u kompleksnom prostoru su dijagonalizabilni: normalni, invertibilni, unitarni, ortogonalne projekcije.
8.) Što za operatore A i B NE vrijedi na kompleksnom prostoru: (a+B)* = B* + A*, ((lambda)A)* = lambda(A*), (AB)* = A*B*, (A*)* = A.
Napišem i drugi dio mrvu kasnije, sad mi se žuri. 
_________________
Weit von hier fällt Gold von den Sternen
|
|
| [Vrh] |
|
Ally
Forumaš(ica)

Pridružen/a: 15. 04. 2008. (19:57:23)
Postovi: (7F)16
Spol: 
|
 Postano: 11:13 pon, 7. 7. 2008 Naslov: Postano: 11:13 pon, 7. 7. 2008 Naslov: |
    |
|
|
Da se i ja pridruzim s nekim pitanjima:
[b]Pitalice DA/NE:[/b]
1.) Algebarska kratnost uvijek je manja ili jednaka geometrijskoj kratnosti.
2.) Ako su V, W i Z vektorski prostori takvi da je V okomito na W, a W okomito na Z, tada je nuzno V okomito na Z.
Mislim da ih je bilo jos, al ne mogu se sjetit..
[b]Teorijski dio:[/b]
1.) Precizno definiraj pojmove rang i defekt, te iskazi teorem o rangu i defektu.
2.) precizno definiraj minimalni polinom.
3.) Iskazi Rieszov teorem reprezentacije
4.) Definiraj Besselovu nejednakost. Kada vrijedi jednakost?
5.) Zadana je matrica:
2 1 0 0
0 2 0 0
0 0 2 0
0 0 0 1
Odredi minimalni polinom.
6.) Na R3[X] (prostor polinoma stupnja manjeg ili jednakog 3) napisi:
a) napisi matricu operatora p-->p' + 1 u standardnoj bazi
b) Pokazi da je S:={peR3[X]: integral od 0 do 1 p(x)dx=0 } potprostor i odredi mu jednu bazu.
7.) Odredi matricu operatora cije su svojstvene vrijednosti 1 i 4, a sv.vektori (3,1) i (2,1)
8.) Dokazi da je i-ti redak invertibilne matrice A ortogonalan na j-ti stupac matrice A^-1 za i razlicito od j.
9.) Neka je A lin.operator na V, a W<=V potprostor invarijantan na A. Pokazi da za svaki polinom p potprostor W invarijantan i na operator p(A).
10.) Neka je V konacnodimenzionalan vektorski prostor sa danim skalarnim produktom <. | . >[size=7]1[/size]. Ako je <.|.>[size=7]2[/size] bilo koji drugi skalarni produkt na V pokazi da postoji jedinstven pozitivno definintan AeLin(V;V) takav da je <.|.>[size=7]1[/size]=<A.|.>[size=7]2[/size]
11.) Precizno definiraj pozitivno definintan linearan operator.
Da se i ja pridruzim s nekim pitanjima:
Pitalice DA/NE:
1.) Algebarska kratnost uvijek je manja ili jednaka geometrijskoj kratnosti.
2.) Ako su V, W i Z vektorski prostori takvi da je V okomito na W, a W okomito na Z, tada je nuzno V okomito na Z.
Mislim da ih je bilo jos, al ne mogu se sjetit..
Teorijski dio:
1.) Precizno definiraj pojmove rang i defekt, te iskazi teorem o rangu i defektu.
2.) precizno definiraj minimalni polinom.
3.) Iskazi Rieszov teorem reprezentacije
4.) Definiraj Besselovu nejednakost. Kada vrijedi jednakost?
5.) Zadana je matrica:
2 1 0 0
0 2 0 0
0 0 2 0
0 0 0 1
Odredi minimalni polinom.
6.) Na R3[X] (prostor polinoma stupnja manjeg ili jednakog 3) napisi:
a) napisi matricu operatora p→p' + 1 u standardnoj bazi
b) Pokazi da je S:={peR3[X]: integral od 0 do 1 p(x)dx=0 } potprostor i odredi mu jednu bazu.
7.) Odredi matricu operatora cije su svojstvene vrijednosti 1 i 4, a sv.vektori (3,1) i (2,1)
8.) Dokazi da je i-ti redak invertibilne matrice A ortogonalan na j-ti stupac matrice A^-1 za i razlicito od j.
9.) Neka je A lin.operator na V, a W⇐V potprostor invarijantan na A. Pokazi da za svaki polinom p potprostor W invarijantan i na operator p(A).
10.) Neka je V konacnodimenzionalan vektorski prostor sa danim skalarnim produktom <. | . >1. Ako je <.|.>2 bilo koji drugi skalarni produkt na V pokazi da postoji jedinstven pozitivno definintan AeLin(V;V) takav da je <.|.>1=<A.|.>2
11.) Precizno definiraj pozitivno definintan linearan operator.
_________________
I just wanna dance..
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
 Postano: 19:21 pon, 7. 7. 2008 Naslov: Postano: 19:21 pon, 7. 7. 2008 Naslov: |
    |
|
|
Ostadoh zaprepaštena usmenim. Teorem 24., u nekim krugovima poznatiji kao najgori. Jedino pitanje. Usmeni je bio gotov kad sam se sjetila cijelog iskaza :oops:
Općenito o pitanjima koja su bila upućena drugima... Pa gradiva i teorema ima stvarno dosta, i puno ekvivalencija i implikacija pa bi se tu dalo postaviti puno teških pitanja i tražiti duže ili kraće dokaze, ali mi se nekako čini da sama pitanja na usmenom nisu bila toliko zahtjevna. Bitno je znati definirati osnovne stvari i onda baratati odnosima među njima. Očekivano, projekcije su bile najčešće spominjanje jer se javljaju na puno mjesta.
Oni koji su rješili onaj sa * su imali to pitanje (nisam sigurna jesu baš svi, ali mislim da su dvojica).
Ne znam kako su se stvari odvijale kasnije.
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
[quote="Lafiel"]Bi mi mogao netko ovo dokazati? :)[/quote]
Znaš da je A * inverz=I. Kad množiš i-ti redak od A sa i-tim stupcem inverza dobiješ 1, a kad množiš i-ti redak sa j-otim stupcem (pri čemu su i i j različiti) dobiješ 0. Zato su ortogonalni.
Stručnije ne znam napisati. Ja sam to tako opisno.
Da, moglo bi se sa Kronekerovim simbolom.
Ostadoh zaprepaštena usmenim. Teorem 24., u nekim krugovima poznatiji kao najgori. Jedino pitanje. Usmeni je bio gotov kad sam se sjetila cijelog iskaza 
Općenito o pitanjima koja su bila upućena drugima... Pa gradiva i teorema ima stvarno dosta, i puno ekvivalencija i implikacija pa bi se tu dalo postaviti puno teških pitanja i tražiti duže ili kraće dokaze, ali mi se nekako čini da sama pitanja na usmenom nisu bila toliko zahtjevna. Bitno je znati definirati osnovne stvari i onda baratati odnosima među njima. Očekivano, projekcije su bile najčešće spominjanje jer se javljaju na puno mjesta.
Oni koji su rješili onaj sa * su imali to pitanje (nisam sigurna jesu baš svi, ali mislim da su dvojica).
Ne znam kako su se stvari odvijale kasnije.
Added after 5 minutes:
| Lafiel (napisa): | Bi mi mogao netko ovo dokazati?  |
Znaš da je A * inverz=I. Kad množiš i-ti redak od A sa i-tim stupcem inverza dobiješ 1, a kad množiš i-ti redak sa j-otim stupcem (pri čemu su i i j različiti) dobiješ 0. Zato su ortogonalni.
Stručnije ne znam napisati. Ja sam to tako opisno.
Da, moglo bi se sa Kronekerovim simbolom.
_________________ mladac: e.k.s. je možda 8%, moje znanje ni toliko  |
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
yimpa
Forumaš(ica)
Pridružen/a: 18. 01. 2008. (23:56:37)
Postovi: (26)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
amorphis
Forumaš(ica)


Pridružen/a: 10. 02. 2007. (23:15:13)
Postovi: (101)16
Lokacija: zg
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
Ally
Forumaš(ica)

Pridružen/a: 15. 04. 2008. (19:57:23)
Postovi: (7F)16
Spol: 
|
|
| [Vrh] |
|
__MP__
Forumaš(ica)

Pridružen/a: 11. 02. 2008. (21:46:38)
Postovi: (1F)16
Lokacija: Požega
|
|
| [Vrh] |
|
kuki
Forumaš(ica)
Pridružen/a: 29. 01. 2008. (20:49:12)
Postovi: (8)16
|
|
| [Vrh] |
|
tammy
Forumaš(ica)

Pridružen/a: 02. 07. 2007. (20:37:10)
Postovi: (197)16
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
i v a n č i c a
Forumaš(ica)
Pridružen/a: 15. 02. 2007. (10:33:16)
Postovi: (2E)16
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
 Postano: 15:21 čet, 17. 7. 2008 Naslov: Postano: 15:21 čet, 17. 7. 2008 Naslov: |
    |
|
|
Raspored usmenih ispita za 18.7.
(u 110 ako ne bude drugačije oglašeno)
8:15
Ankica Radovanović, Karlo Peček, Ivana Pavlek, Petar Paradžik
9:00
Tamara Međimorec, Roža Obućina, Nikola Marinić, Amalija Marelja
10:00
Dario Maltarski, Mandalena Pranjić, Karolina Kolarić, Ivana Zlodi
14:15
Tina Škrtić, Josip Perić, Antonija Mamut, Siniša Pogačić, Ivan Petrunić
15:00
Petar Sirković, Dobrila Roksandić, Josip Perković, Mihaela Poljak
16:00
Igor Tomašić, Anela Pavelić, Željka Žilnik, Adam Nikšić, Aleksandar Milković
Slobodno se zamijenite za termine s kolegama.
- Nenad Antonić
Raspored usmenih ispita za 18.7.
(u 110 ako ne bude drugačije oglašeno)
8:15
Ankica Radovanović, Karlo Peček, Ivana Pavlek, Petar Paradžik
9:00
Tamara Međimorec, Roža Obućina, Nikola Marinić, Amalija Marelja
10:00
Dario Maltarski, Mandalena Pranjić, Karolina Kolarić, Ivana Zlodi
14:15
Tina Škrtić, Josip Perić, Antonija Mamut, Siniša Pogačić, Ivan Petrunić
15:00
Petar Sirković, Dobrila Roksandić, Josip Perković, Mihaela Poljak
16:00
Igor Tomašić, Anela Pavelić, Željka Žilnik, Adam Nikšić, Aleksandar Milković
Slobodno se zamijenite za termine s kolegama.
- Nenad Antonić
|
|
| [Vrh] |
|
i v a n č i c a
Forumaš(ica)

Pridružen/a: 15. 02. 2007. (10:33:16)
Postovi: (2E)16
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
|
| [Vrh] |
|
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
|
| [Vrh] |
|
|














