| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:31 uto, 8. 7. 2008 Naslov: Postano: 17:31 uto, 8. 7. 2008 Naslov: |
    |
|
|
Tu prvo na pamet pada indukcija... za
n=0 [latex]rez=\sqrt{1}=1[/latex]
n=1 [latex]rez=\sqrt{49}=7[/latex]
n=2 [latex]rez=\sqrt{4489}=67[/latex]
n=3 [latex]rez=\sqrt{444889}=667[/latex]
Sad to treba lijepo povezat u formulu, koju ja baš ne vidim, ali vidi se pravilnost, pod korijenom su n četvorka, n-1 osmica i jedna devetka, a kao rezultat su n-1 šestica i jedna sedmica. Sad to lijepo zapisat pa probat dokazat indukcijom...
p.s. Indukcija je ona metoda kojom si dokazo koliki je zbroj prvih n prirodnih brojeva. Pokažeš za bazu da vrijedi formula, pretpostaviš da vrijedi za neki n pa dokažeš da vrijedi i za n+1. ;)
Tu prvo na pamet pada indukcija... za
n=0 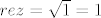
n=1 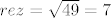
n=2 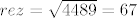
n=3 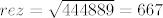
Sad to treba lijepo povezat u formulu, koju ja baš ne vidim, ali vidi se pravilnost, pod korijenom su n četvorka, n-1 osmica i jedna devetka, a kao rezultat su n-1 šestica i jedna sedmica. Sad to lijepo zapisat pa probat dokazat indukcijom...
p.s. Indukcija je ona metoda kojom si dokazo koliki je zbroj prvih n prirodnih brojeva. Pokažeš za bazu da vrijedi formula, pretpostaviš da vrijedi za neki n pa dokažeš da vrijedi i za n+1. 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
 Postano: 17:51 uto, 8. 7. 2008 Naslov: Postano: 17:51 uto, 8. 7. 2008 Naslov: |
    |
|
|
[quote="Luuka"]Tu prvo na pamet pada indukcija... za
n=0 [latex]rez=\sqrt{1}=1[/latex]
n=1 [latex]rez=\sqrt{49}=7[/latex]
n=2 [latex]rez=\sqrt{4489}=67[/latex]
n=3 [latex]rez=\sqrt{444889}=667[/latex]
Sad to treba lijepo povezat u formulu, koju ja baš ne vidim, ali vidi se pravilnost, pod korijenom su n četvorka, n-1 osmica i jedna devetka, a kao rezultat su n-1 šestica i jedna sedmica. Sad to lijepo zapisat pa probat dokazat indukcijom...
p.s. Indukcija je ona metoda kojom si dokazo koliki je zbroj prvih n prirodnih brojeva. Pokažeš za bazu da vrijedi formula, pretpostaviš da vrijedi za neki n pa dokažeš da vrijedi i za n+1. ;)[/quote]
Da da...naučio sam indukciju...samo ne znam povezati...a ovo što je goc napisao nije baš da kužim...
| Luuka (napisa): | Tu prvo na pamet pada indukcija... za
n=0 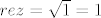
n=1 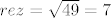
n=2 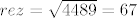
n=3 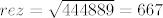
Sad to treba lijepo povezat u formulu, koju ja baš ne vidim, ali vidi se pravilnost, pod korijenom su n četvorka, n-1 osmica i jedna devetka, a kao rezultat su n-1 šestica i jedna sedmica. Sad to lijepo zapisat pa probat dokazat indukcijom...
p.s. Indukcija je ona metoda kojom si dokazo koliki je zbroj prvih n prirodnih brojeva. Pokažeš za bazu da vrijedi formula, pretpostaviš da vrijedi za neki n pa dokažeš da vrijedi i za n+1.  |
Da da...naučio sam indukciju...samo ne znam povezati...a ovo što je goc napisao nije baš da kužim...
_________________
Čovjek koji ne mijenja mišljenje voli sebe više nego istinu!
Pomoću logike dokazujemo, ali pomoću intuicije otkrivamo!
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
 Postano: 17:53 ned, 19. 10. 2008 Naslov: Postano: 17:53 ned, 19. 10. 2008 Naslov: |
    |
|
|
Probao sam dokazati da je [latex]\sqrt{n+ \sqrt{n} }[/latex] iracionalan broj za svaki n E(element) od [b]N[/b].Pa bih vas zamolio da mi pomognete jer sam zapeo na jednom dijelu, a i naravno ispravite jer je lako moguće da sam negdje pogriješio.
Pretpostavio sam suprotno, [latex]\sqrt{n+ \sqrt{n} } = \frac {x} {y}[/latex], pa kvadrirao
[latex]n+ \sqrt{n} = \frac {x^2} {y^2}[/latex]
[latex]y^2(n+\sqrt{n})=x^2[/latex]
[latex]n+\sqrt{n}[/latex] je uvijek oblika 2k, ako je n oblika [latex]n^2[/latex].
onda sam dobio [latex]2ky^2=x^2[/latex], vidi se da je [latex]x^2[/latex] paran broj, pa je oblika 2k. onda imamo [latex]2ky^2=4k^2[/latex], [latex]k(y^2-2)=0[/latex], kada je [latex]k=0[/latex] i [latex]y=\sqrt {2}[/latex]
... ne znam kako dalje. Unaprijed Hvala! :D
Probao sam dokazati da je 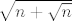 iracionalan broj za svaki n E(element) od N.Pa bih vas zamolio da mi pomognete jer sam zapeo na jednom dijelu, a i naravno ispravite jer je lako moguće da sam negdje pogriješio. iracionalan broj za svaki n E(element) od N.Pa bih vas zamolio da mi pomognete jer sam zapeo na jednom dijelu, a i naravno ispravite jer je lako moguće da sam negdje pogriješio.
Pretpostavio sam suprotno, 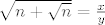 , pa kvadrirao , pa kvadrirao
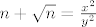
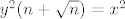
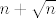 je uvijek oblika 2k, ako je n oblika je uvijek oblika 2k, ako je n oblika 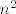 . .
onda sam dobio 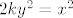 , vidi se da je , vidi se da je 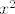 paran broj, pa je oblika 2k. onda imamo paran broj, pa je oblika 2k. onda imamo 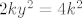 , , 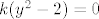 , kada je , kada je 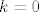 i i 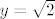
... ne znam kako dalje. Unaprijed Hvala! 
_________________
Čovjek koji ne mijenja mišljenje voli sebe više nego istinu!
Pomoću logike dokazujemo, ali pomoću intuicije otkrivamo!
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
behemont
Forumaš(ica)

Pridružen/a: 12. 02. 2008. (21:21:19)
Postovi: (124)16
Spol: 
|
 Postano: 13:40 pon, 20. 10. 2008 Naslov: Postano: 13:40 pon, 20. 10. 2008 Naslov: |
    |
|
|
[quote="tuv0k"]Probao sam dokazati da je [latex]\sqrt{n+ \sqrt{n} }[/latex] iracionalan broj za svaki n E(element) od [b]N[/b].Pa bih vas zamolio da mi pomognete jer sam zapeo na jednom dijelu, a i naravno ispravite jer je lako moguće da sam negdje pogriješio.
Pretpostavio sam suprotno, [latex]\sqrt{n+ \sqrt{n} } = \frac {x} {y}[/latex], pa kvadrirao
[latex]n+ \sqrt{n} = \frac {x^2} {y^2}[/latex]
[latex]y^2(n+\sqrt{n})=x^2[/latex]
[latex]n+\sqrt{n}[/latex] je uvijek oblika 2k, ako je n oblika [latex]n^2[/latex].
onda sam dobio [latex]2ky^2=x^2[/latex], vidi se da je [latex]x^2[/latex] paran broj, pa je oblika 2k. onda imamo [latex]2ky^2=4k^2[/latex], [latex]k(y^2-2)=0[/latex], kada je [latex]k=0[/latex] i [latex]y=\sqrt {2}[/latex]
... ne znam kako dalje. Unaprijed Hvala! :D[/quote]
Ako je [latex]n+\sqrt{n}=2k[/latex], taj [latex]k[/latex] ti nije isti broj kao i ovaj kod [latex]x=2k[/latex]. Treba biti [latex]x=2l[/latex], ili neko drugo slovo. Nadam se da razumijes, malo sam nespretno napisao.
A kao sto ti je rafael rekao, ako je [latex]n+\sqrt{n}[/latex] racionalan, onda je nuzno i prirodan. Pa pretpostavimo da postoji [latex]n,m\in N[/latex] takvi da je [latex]n+\sqrt{n}=m^2[/latex]. Ocito je [latex]n=k^2[/latex] za neki [latex]k\in N[/latex]. Ali ovo posljednje ocito nema rjesenja jer je [latex]k^2<k^2+k<(k+1)^2 \forall k\in N[/latex].
| tuv0k (napisa): | Probao sam dokazati da je 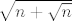 iracionalan broj za svaki n E(element) od N.Pa bih vas zamolio da mi pomognete jer sam zapeo na jednom dijelu, a i naravno ispravite jer je lako moguće da sam negdje pogriješio. iracionalan broj za svaki n E(element) od N.Pa bih vas zamolio da mi pomognete jer sam zapeo na jednom dijelu, a i naravno ispravite jer je lako moguće da sam negdje pogriješio.
Pretpostavio sam suprotno, 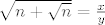 , pa kvadrirao , pa kvadrirao
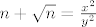
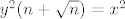
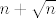 je uvijek oblika 2k, ako je n oblika je uvijek oblika 2k, ako je n oblika 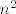 . .
onda sam dobio 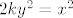 , vidi se da je , vidi se da je 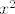 paran broj, pa je oblika 2k. onda imamo paran broj, pa je oblika 2k. onda imamo 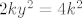 , , 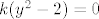 , kada je , kada je 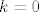 i i 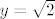
... ne znam kako dalje. Unaprijed Hvala!  |
Ako je 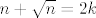 , taj , taj  ti nije isti broj kao i ovaj kod ti nije isti broj kao i ovaj kod 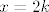 . Treba biti . Treba biti 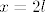 , ili neko drugo slovo. Nadam se da razumijes, malo sam nespretno napisao. , ili neko drugo slovo. Nadam se da razumijes, malo sam nespretno napisao.
A kao sto ti je rafael rekao, ako je 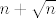 racionalan, onda je nuzno i prirodan. Pa pretpostavimo da postoji racionalan, onda je nuzno i prirodan. Pa pretpostavimo da postoji 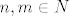 takvi da je takvi da je 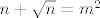 . Ocito je . Ocito je 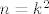 za neki za neki  . Ali ovo posljednje ocito nema rjesenja jer je . Ali ovo posljednje ocito nema rjesenja jer je 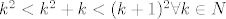 . .
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
|
| [Vrh] |
|
mea
Forumaš(ica)

Pridružen/a: 10. 12. 2002. (13:22:34)
Postovi: (1F0)16
|
|
| [Vrh] |
|
tuv0k
Forumaš(ica)

Pridružen/a: 21. 06. 2008. (22:42:03)
Postovi: (40)16
|
 Postano: 19:41 sri, 12. 11. 2008 Naslov: Postano: 19:41 sri, 12. 11. 2008 Naslov: |
    |
|
|
Evo još jedno pitanje...Nadam se da nije problem... Radi se o tangensu u pi/2.
Ako se gleda po kružnici, pravac koji prolazi kroz ishodište KS-a neće nikada sjeći tangentu(tangens). Dakle, on je neodređen.
Ako se gleda po formuli [latex]\tan x = \frac{\sin x}{\cos x}[/latex] dođe da je [latex]\frac{1}{0}= \pm \infty[/latex].
E sada, mene zanima, kako neki broj podijeljen sa 0 može biti beskonačan, i što uopće znači beskonačnost?
Evo još jedno pitanje...Nadam se da nije problem... Radi se o tangensu u pi/2.
Ako se gleda po kružnici, pravac koji prolazi kroz ishodište KS-a neće nikada sjeći tangentu(tangens). Dakle, on je neodređen.
Ako se gleda po formuli 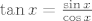 dođe da je dođe da je 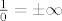 . .
E sada, mene zanima, kako neki broj podijeljen sa 0 može biti beskonačan, i što uopće znači beskonačnost?
_________________
Čovjek koji ne mijenja mišljenje voli sebe više nego istinu!
Pomoću logike dokazujemo, ali pomoću intuicije otkrivamo!
|
|
| [Vrh] |
|
|











