Završni ispit (informacija)

[Ivecus]

Jel zna netko možda kak ce izgledat završni ispit, bilo kakva informacija nebi bila na odmet, ono za drugi kolokvij je pomoglo...

_________________
Mihi est propositum in taberna mori!

[tihana]

ja sam čula da će (između ostalog) biti rotaciona tijela i dA

pogledaj si završni iz difrafa a ako još netko ovdje napiše što je saznao - super

_________________
I aim to misbehave

[ivanzub]

dA?

Added after 54 seconds:

[tihana]

[the maja]

ja sam poslala mail prof. Hanzer i rekla je da će tek danas dobiti predložene zadatke od strane asistenata, ali da će koncept biti sličan prošlogodišnjem što se tiče omjera teorije i zadataka. Pitala sam i hoće li biti rot.plohe, jer ih nismo radili, i rekla je da će re reći asistentima da ih nismo savladali
eto, to je to

[desire]

Jel bi mogao netko pokazat kako se dokazuje da je f:[0,1]→R, f(x)=x^2 skup mjere 0 u R^2? (to je prvi zad iz proslogodisnjeg zavrsnog)

Hvala

_________________

[Luuka]

Tu možeš ko u dokazu onog tm da je graf int fje skup mjere 0.

Dakle, zadaš E>0.

I sad, poošto je f integrabilna, postoji subdivizija t.d.
S(P)-s(P)<E , nakon raspisivanja imaš



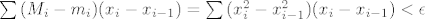
(zadnji korak nije ni bitan), imamo pravokutnike [Mi,mi] x [xi,x(i-1)] čija je ukupna površina manja od E

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[desire]

Hvala Luuka.

_________________

[Gost]

Je li može pomoć oko 7. zadatka s drugog kolokvija?
http://web.math.hr/nastava/difraf/int/2007-08/IFVVkol2_2008.pdf
Unaprijed hvala!!!

[lunjo]

jel bi mogao netko rijesit 5. zad sa ovog sad zavrsnog, please..

[ivo34]

Pridruzujem se molbi..

_________________


http://www.youtube.com/watch?v=KEn1hdmUPdM&feature=related

[putanja]

pa ja sam to ovako: kazes da ogranicen skup (a ovaj je ogranicen jer je omeden zadanim funkcijama) ima povrsinu ako mu je rub skup mjere nula.. a rub mu je unija grafova zadanih funkcija, te funkcije su neprekidne na segmentu (za rubove segmenta uzmes x-te koordinate sjecista) i pokazes da je graf svake od njih skup povrsine nula (to ti je napravljano u primjeru 6.3 u skripti za opcenito neku f-ju), a skup povrsine nula je i mjere nula(to se vidi iz definicije)... unija skupova mjere nula je ponovo skup mjere nula, dakle rub naseg skupa, kao unija skupova mjere nula, je skup mjere nula, slijedi: zadani skup ima povrsinu,interior omedenog skupa ciji rub je skup mjere nula takoder ima povrsinu i ona je jednaka povrsini skupa...
nadam se da nisam previse spetljala...

[lunjo]

nisi, sve sam razumila! hvala ti

[desire]

Rezultati.

_________________

[Gost]

Rezultati su porazavajuci, nije li malo prestrogo ocijenjeno?!

[andreao]

pa prema ovom šta ja vidim nisu prestrogo ocjenjivali. gledam baš svoje rezultate i možda su čak išli maksimalno na ruku kolko su mogli.
al neznam kakve ti bodove imaš, tak da vjerojatno onda imamo drugačije poglede na završni.

_________________

[Gost]

Ako sam nesto zeznula u integralima koji do sad al stvarno znam rjesavat ( a dobila manje od 50% na tim zadacima), ona sam racunala na 6. zad koji sam potpuno rijesila! A dali su mi par bodova na tome! I nisam jedina koja se cudi...

[desire]

Meni se isto cini ok. Sto sam rijesila to sam i dobila u sto nisam bas bila sigurna iz toga nemam bas puno bodova, ali nije ni da nemam uopce...

Edit: da, na 6. ni ja nemam bas puno bodova iako sam ga rijesila skoro cijelog, ali to sam si ja protumacila kao da sam ocito nesto ipak krivo napisala.

_________________

[Gost]

Preostaje mi samo da upitam kada su zalbe ako ce ih uopce biti? Asistenti?

[desire]