| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Nesi
Inventar Foruma
(Moderator)


Pridružen/a: 14. 10. 2002. (14:27:35)
Postovi: (E68)16
Spol: 
Sarma: -
|
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 17:38 sri, 18. 2. 2004 Naslov: Re: adjunkta Postano: 17:38 sri, 18. 2. 2004 Naslov: Re: adjunkta |
    |
|
|
[quote="Nesi"][quote="Anonymous"]Moze li mi netko ukratko objasnit sto je adjunkta?? :oops: :?: :?: :?:[/quote]
adjunkta = inverz * determinanta
sluzi da dobijemo inverz => inverz = 1/det * adjunkta
neka je matrica reda n×n (regularna ofkors, inace nema inverz :g:)
elementi adjunkte se definiraju ovak:
element na mjestu [color=indigo] [b][J,I][/b][/color] je determinanta matrice reda (n-1)×(n-1)
koju dobijemo tako da u matrici reda n×n prekrizimo element [color=indigo][b][I,J][/b][/color] te redak i stupac u kojem se taj element nalazi
dakle, ne zaboraviti da je stvar [color=indigo][b]transponirana[/b][/color] :!:[/quote]
Khm.
Prvo, zaboravila si predznak (s kojim se množi svaka pojedina determinanta), koji je (-1)^(i+j) za poziciju (i,j) u matrici.
Drugo, i singularne matrice imaju adjunktu (definiranu na isti način). To što se ta adjunkta ne može podijeliti s determinantom (=0) da se dobije inverz, nije njen problem. :-)
| Nesi (napisa): | | Anonymous (napisa): | Moze li mi netko ukratko objasnit sto je adjunkta??     |
adjunkta = inverz * determinanta
sluzi da dobijemo inverz ⇒ inverz = 1/det * adjunkta
neka je matrica reda n×n (regularna ofkors, inace nema inverz  ) )
elementi adjunkte se definiraju ovak:
element na mjestu [J,I] je determinanta matrice reda (n-1)×(n-1)
koju dobijemo tako da u matrici reda n×n prekrizimo element [I,J] te redak i stupac u kojem se taj element nalazi
dakle, ne zaboraviti da je stvar transponirana  |
Khm.
Prvo, zaboravila si predznak (s kojim se množi svaka pojedina determinanta), koji je (-1)^(i+j) za poziciju (i,j) u matrici.
Drugo, i singularne matrice imaju adjunktu (definiranu na isti način). To što se ta adjunkta ne može podijeliti s determinantom (=0) da se dobije inverz, nije njen problem. 
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
jakov
Forumaš(ica)

Pridružen/a: 30. 08. 2006. (20:03:41)
Postovi: (47)16
Spol: 
Lokacija: evo me doma
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
 Postano: 15:55 sub, 9. 2. 2008 Naslov: Postano: 15:55 sub, 9. 2. 2008 Naslov: |
    |
|
|
[quote="Masiela"]Imaš kakve materijale s vježbi? :?
Konkretno ovaj primjer 1*4-3*2=-1[/quote]
Ma znam "klasično", tj po laplaceu zračunat determinantu. Nije to bed. Neg sam ljosnuo prošle godine na usmenom, jer nisam znao zračunat determinantu po definiciji.
Dakle, napraviti skup permutacija, pa one inverzije, pa -1 na nešto...
Da znam ne bih pitao :P
Ili neki onda kompliciraniji primjer, generic 3x3 matrica možda...
| Masiela (napisa): | Imaš kakve materijale s vježbi? 
Konkretno ovaj primjer 1*4-3*2=-1 |
Ma znam "klasično", tj po laplaceu zračunat determinantu. Nije to bed. Neg sam ljosnuo prošle godine na usmenom, jer nisam znao zračunat determinantu po definiciji.
Dakle, napraviti skup permutacija, pa one inverzije, pa -1 na nešto...
Da znam ne bih pitao 
Ili neki onda kompliciraniji primjer, generic 3x3 matrica možda...
|
|
| [Vrh] |
|
ß
Forumaš(ica)
Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
 Postano: 16:04 sub, 9. 2. 2008 Naslov: Postano: 16:04 sub, 9. 2. 2008 Naslov: |
    |
|
|
[quote="punio4"]Hmhm... Dok smo već kod determinanti...
Znam ja definiciju determinante, no nemam pojma kako bi to u praksi izgledalo.
Može li mi netko objasniti kako bi išlo računanje determinante po definiciji od, recimo:
[latex]\begin{vmatrix}
1 & 2 \\
3 & 4 \\
\end{vmatrix}[/latex][/quote]
Ne vjerujem da ćeš iz determinante 2x2 raspisom po definiciji išta više shvatiti... Naime, kaže wikipedia ovako (kradem latex jer mi se ne da ispisivat svoj :D )
[latex]\det(A) = \sum_{\sigma \in S_n} \sgn(\sigma) \prod_{i=1}^n A_[/latex]
Sad, ovaj komadić [latex]\sigma \in S_n[/latex] označava proizvoljnu permutaciju n-skupa {1,2,...n}, odnosno [latex]\sigma[/latex] je bilo koja bijekcija sa {1,2,..n} u {1,2,...n}. Ti sumiraš po [b]svim[/b] postojećim bijekcijama, a za n=2 ih je lako ispisati, jer su očito samo dvije:
[latex]\sigma_1(1)=1,\sigma_1(2)=2[/latex]
[latex]\sigma_2(1)=2,\sigma_2(2)=1[/latex]
kad staviš prvu permutaciju, množiš [latex]a_{11}[/latex] i [latex]a_{22}[/latex], jer su indeksi jednaki [latex]i,\sigma(i)[/latex].
za drugu permutaciju, množiš [latex]a_{12}[/latex] i [latex]a_{21}[/latex], po istom principu.
Kad zbrajaš, trebaš staviti ispred druge potencije predznak minus (to je onaj komad [latex]sgn(\sigma)[/latex]). To se dobije jer ta permutacija ima neparan broj inverzija (jednu), pretpostavljam da ste radili na predavanju kako se to određuje, a meni je mukotrpno raspisivat :oops: . Al u svakom slučaju, kad ideš određivat za determinante višeg reda, ako "lijepo" raspišeš te permutacije, bit će parna-neparna-parna-neparna-itd, pa ćeš samo ove umnoške od po n članova naizmjence zbrajat i množit. Dakle, na kraju imaš za 2-determinantu poznati izraz: [latex]a_{11}a_{22}-a_{12}a_{21}[/latex].
Ukratko, isti postupak za 3x3:
-imaš 6 permutacija, skraćeno, one izgledaju ovako: 123, 132, 213, 231, 312, 321.
-one se "pretvore" u: [latex]a_{11}a_{22}a_{33}, a_{11}a_{23}a_{32}, ...[/latex]
-predznaci su im naizmjence + i -
-sve to sumiraš:
[latex]{\it a_{11}}\,{\it a_{22}}\,{\it a_{33}}-{\it a_{12}}\,{\it a_{21}}
\,{\it a_{33}}-{\it a_{11}}\,{\it a_{23}}\,{\it a_{32}}+{\it a_{13}}
\,{\it a_{21}}\,{\it a_{32}}+{\it a_{12}}\,{\it a_{23}}\,
{\it a_{31}}-{\it a_{13}}\,{\it a_{22}}\,{\it a_{31}}[/latex]
i to je determinanta. Nadam se da je bar nešto od ovog bilo shvatljivo :D
EDIT: Ova zadnja linija koja bi trebala označavat determinantu ima malo drugačiji raspored sumanada jer sam je ubacio u maximu da mi ispiše latex kod, a ona očito ima drugačiji raspored. Uglavnom, ako ih porazmjestiš po onim permutacijama koje sam gore napisao, trebalo bi ići naizmjence plus/minus.
| punio4 (napisa): | Hmhm... Dok smo već kod determinanti...
Znam ja definiciju determinante, no nemam pojma kako bi to u praksi izgledalo.
Može li mi netko objasniti kako bi išlo računanje determinante po definiciji od, recimo:
 |
Ne vjerujem da ćeš iz determinante 2x2 raspisom po definiciji išta više shvatiti... Naime, kaže wikipedia ovako (kradem latex jer mi se ne da ispisivat svoj  ) )
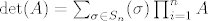
Sad, ovaj komadić 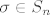 označava proizvoljnu permutaciju n-skupa {1,2,...n}, odnosno označava proizvoljnu permutaciju n-skupa {1,2,...n}, odnosno  je bilo koja bijekcija sa {1,2,..n} u {1,2,...n}. Ti sumiraš po svim postojećim bijekcijama, a za n=2 ih je lako ispisati, jer su očito samo dvije: je bilo koja bijekcija sa {1,2,..n} u {1,2,...n}. Ti sumiraš po svim postojećim bijekcijama, a za n=2 ih je lako ispisati, jer su očito samo dvije:
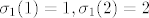
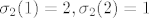
kad staviš prvu permutaciju, množiš 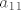 i i 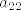 , jer su indeksi jednaki , jer su indeksi jednaki 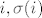 . .
za drugu permutaciju, množiš 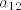 i i 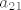 , po istom principu. , po istom principu.
Kad zbrajaš, trebaš staviti ispred druge potencije predznak minus (to je onaj komad 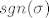 ). To se dobije jer ta permutacija ima neparan broj inverzija (jednu), pretpostavljam da ste radili na predavanju kako se to određuje, a meni je mukotrpno raspisivat ). To se dobije jer ta permutacija ima neparan broj inverzija (jednu), pretpostavljam da ste radili na predavanju kako se to određuje, a meni je mukotrpno raspisivat  . Al u svakom slučaju, kad ideš određivat za determinante višeg reda, ako "lijepo" raspišeš te permutacije, bit će parna-neparna-parna-neparna-itd, pa ćeš samo ove umnoške od po n članova naizmjence zbrajat i množit. Dakle, na kraju imaš za 2-determinantu poznati izraz: . Al u svakom slučaju, kad ideš određivat za determinante višeg reda, ako "lijepo" raspišeš te permutacije, bit će parna-neparna-parna-neparna-itd, pa ćeš samo ove umnoške od po n članova naizmjence zbrajat i množit. Dakle, na kraju imaš za 2-determinantu poznati izraz: 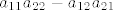 . .
Ukratko, isti postupak za 3x3:
-imaš 6 permutacija, skraćeno, one izgledaju ovako: 123, 132, 213, 231, 312, 321.
-one se "pretvore" u: 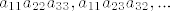
-predznaci su im naizmjence + i -
-sve to sumiraš:
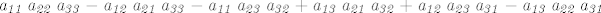
i to je determinanta. Nadam se da je bar nešto od ovog bilo shvatljivo 
EDIT: Ova zadnja linija koja bi trebala označavat determinantu ima malo drugačiji raspored sumanada jer sam je ubacio u maximu da mi ispiše latex kod, a ona očito ima drugačiji raspored. Uglavnom, ako ih porazmjestiš po onim permutacijama koje sam gore napisao, trebalo bi ići naizmjence plus/minus.
_________________
Devious movements in your eyes moved me from relief
Breath comes out white clouds with your lies
and filters through me
|
|
| [Vrh] |
|
punio4
Forumaš(ica)


Pridružen/a: 08. 11. 2006. (18:32:34)
Postovi: (120)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ekatarina
Forumaš(ica)

Pridružen/a: 25. 11. 2007. (19:22:50)
Postovi: (161)16
Spol: 
|
|
| [Vrh] |
|
.bubamara.
Forumaš(ica)
Pridružen/a: 03. 10. 2007. (17:32:18)
Postovi: (4E)16
Spol: 
|
|
| [Vrh] |
|
|















