| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
 Postano: 10:27 pet, 26. 9. 2008 Naslov: O sumi reda Postano: 10:27 pet, 26. 9. 2008 Naslov: O sumi reda |
    |
|
|
Upravo mi je "pala na pamet" slijedeća slutnja:
Neka je a niz a: [b]N[/b] -> ¸{1,2,3,4,5,6,7,8,9}.
Da li je tada suma reda kojem je opći član broj ((-1)^n)(a(n))/n iracionalan broj?
Da li je netko ovdje sposoban dokazati da je tvrdnja istinita ili pronaći protuprimjer u slučaju da nije? Ili barem dati natuknice kojim putem i kako ići? Ja nemam nekih "velikih" ideja. Barem vjerujem da nemam. Zasad.
Upravo mi je "pala na pamet" slijedeća slutnja:
Neka je a niz a: N → ¸{1,2,3,4,5,6,7,8,9}.
Da li je tada suma reda kojem je opći član broj ((-1)^n)(a(n))/n iracionalan broj?
Da li je netko ovdje sposoban dokazati da je tvrdnja istinita ili pronaći protuprimjer u slučaju da nije? Ili barem dati natuknice kojim putem i kako ići? Ja nemam nekih "velikih" ideja. Barem vjerujem da nemam. Zasad.
_________________
Look at every path closely and deliberately. Try it as many times as you think necessary. Then ask yourself,
and yourself alone, one question . . . Does this path have a heart? If it does, the path is good; if it doesn’t it is of no use.
Carlos Castaneda, The Teachings of Don juan
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 18:44 pet, 26. 9. 2008 Naslov: Postano: 18:44 pet, 26. 9. 2008 Naslov: |
    |
|
|
Tesko! Ako cak definiras niz slucajnih varijabli [latex](A_n:n\in\mathbb{N})[/latex] koje su uniformno distribuirane na skupu [latex]\{1,\dots,9\}[/latex] i nezavisne, dogadaj [latex]\displaystyle\{\sum_{n=1}^{\infty}(-1)^n\frac{A_n}{n} \textrm{ konvegira ka iracionalnom broju }\}[/latex] nije element repne [latex]\sigma[/latex]-algebre [latex]\mathcal{F}_{\infty}[/latex] ( ona je dobivena [latex]\displaystyle \mathcal{F}_{\infty}=\cap_{n=1}^{\infty}\sigma (A_n,A_{n+1},\dots )[/latex])
Dakle, ne mozes se bas lagano provuci. Cini mi se jednako "tesko/lagano" kao i orginalna tvrdnja.
Edit: Sorry, malo sam se zaletio, to ipak jest repni dogadaj ( dobijanje prvi n elemenata ne utjece na to konvergira li taj red ka iracionalnom broju ili ne ), dakle barem znas da je vjerojatnost tog dogadaja 0 ili 1, no ne vidim nacin kako utvrditi kolika je to vjerojatnost.
Tesko! Ako cak definiras niz slucajnih varijabli 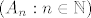 koje su uniformno distribuirane na skupu koje su uniformno distribuirane na skupu  i nezavisne, dogadaj i nezavisne, dogadaj  nije element repne nije element repne  -algebre -algebre 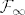 ( ona je dobivena ( ona je dobivena 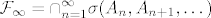 ) )
Dakle, ne mozes se bas lagano provuci. Cini mi se jednako "tesko/lagano" kao i orginalna tvrdnja.
Edit: Sorry, malo sam se zaletio, to ipak jest repni dogadaj ( dobijanje prvi n elemenata ne utjece na to konvergira li taj red ka iracionalnom broju ili ne ), dakle barem znas da je vjerojatnost tog dogadaja 0 ili 1, no ne vidim nacin kako utvrditi kolika je to vjerojatnost.
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 0:01 sub, 27. 9. 2008 Naslov: Postano: 0:01 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="StateOfConsciousness"][quote="goranm"]Pretpostavljam da misliš isključivo na redove koji su konvergenti, jer može se konstruirati niz takav da mu je red divergentan pa se ne može govorit o iracionalnosti sume reda.
Imaš li primjer niza čiji red sa spomenutim općim članom konvergira?[/quote]
Pa svaki red sa gore napisanim općim članom konvergira. Po Leibnitzovom kriteriju.[/quote]
Da, ako se radi o strogo padajućem nizu. Npr ako se definira da je
[latex]a(n)=\left\{
\begin{array}{rl}
1, & n \textrm{ mod }10=0,\\
n \textrm{ mod }10, & \textrm{ina\v{c}e}
\end{array}
\right.
[/latex]
tada je a(11)/11=1/11 i a(22)/22=2/22=1/11 pa niz više nije strogo padajući i ne može se primjeniti Leibnizov kriterij.
Uostalom, ako je niz a(n) takav da svakom parnom n pridruži 1, a svakom neparnom n pridruži -1, onda se dobiva harmonijski red koji sigurno nije konvergentan.
| StateOfConsciousness (napisa): | | goranm (napisa): | Pretpostavljam da misliš isključivo na redove koji su konvergenti, jer može se konstruirati niz takav da mu je red divergentan pa se ne može govorit o iracionalnosti sume reda.
Imaš li primjer niza čiji red sa spomenutim općim članom konvergira? |
Pa svaki red sa gore napisanim općim članom konvergira. Po Leibnitzovom kriteriju. |
Da, ako se radi o strogo padajućem nizu. Npr ako se definira da je
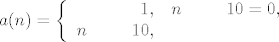
tada je a(11)/11=1/11 i a(22)/22=2/22=1/11 pa niz više nije strogo padajući i ne može se primjeniti Leibnizov kriterij.
Uostalom, ako je niz a(n) takav da svakom parnom n pridruži 1, a svakom neparnom n pridruži -1, onda se dobiva harmonijski red koji sigurno nije konvergentan.
_________________
The Dude Abides
Zadnja promjena: goranm; 0:12 sub, 27. 9. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
 Postano: 0:10 sub, 27. 9. 2008 Naslov: Postano: 0:10 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="goranm"][quote="StateOfConsciousness"][quote="goranm"]Pretpostavljam da misliš isključivo na redove koji su konvergenti, jer može se konstruirati niz takav da mu je red divergentan pa se ne može govorit o iracionalnosti sume reda.
Imaš li primjer niza čiji red sa spomenutim općim članom konvergira?[/quote]
Pa svaki red sa gore napisanim općim članom konvergira. Po Leibnitzovom kriteriju.[/quote]
Da, ako se radi o strogo padajućem nizu. Npr ako se definira da je
[latex]a(n)=\left\{
\begin{array}{rl}
1, & n \textrm{ mod }10=0,\\
n \textrm{ mod }10, & \textrm{ina\v{c}e}
\end{array}
\right.
[/latex]
tada je a(11)/11=1/11 i a(22)/22=2/22=1/11 pa niz više nije strogo padajući i ne može se primjeniti Leibnizov kriterij.[/quote]
U pravu si da ne mora biti strogo padajući ali...vjerujem da je ipak svaki takav niz konvergentan. Ne bih znao pokazati da je tomu tako. Zasad. Napisao si gore da se može konstruirati niz takav da je red divergentan. Daj barem jedan primjer. Dotad ću ja pokušati otkriti neki novi kriterij konvergencije kojim bi pokazao da gornji redovi uvijek konvergiraju ili ću primijeniti Leibnitzov kriterij na malo modificiran red pa ću vidjeti što će biti.
| goranm (napisa): | | StateOfConsciousness (napisa): | | goranm (napisa): | Pretpostavljam da misliš isključivo na redove koji su konvergenti, jer može se konstruirati niz takav da mu je red divergentan pa se ne može govorit o iracionalnosti sume reda.
Imaš li primjer niza čiji red sa spomenutim općim članom konvergira? |
Pa svaki red sa gore napisanim općim članom konvergira. Po Leibnitzovom kriteriju. |
Da, ako se radi o strogo padajućem nizu. Npr ako se definira da je
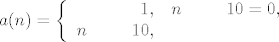
tada je a(11)/11=1/11 i a(22)/22=2/22=1/11 pa niz više nije strogo padajući i ne može se primjeniti Leibnizov kriterij. |
U pravu si da ne mora biti strogo padajući ali...vjerujem da je ipak svaki takav niz konvergentan. Ne bih znao pokazati da je tomu tako. Zasad. Napisao si gore da se može konstruirati niz takav da je red divergentan. Daj barem jedan primjer. Dotad ću ja pokušati otkriti neki novi kriterij konvergencije kojim bi pokazao da gornji redovi uvijek konvergiraju ili ću primijeniti Leibnitzov kriterij na malo modificiran red pa ću vidjeti što će biti.
_________________
Look at every path closely and deliberately. Try it as many times as you think necessary. Then ask yourself,
and yourself alone, one question . . . Does this path have a heart? If it does, the path is good; if it doesn’t it is of no use.
Carlos Castaneda, The Teachings of Don juan
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 2:22 sub, 27. 9. 2008 Naslov: Postano: 2:22 sub, 27. 9. 2008 Naslov: |
    |
|
|
[latex]a_{2k-1} = 1, \quad a_{2k} = 9, \quad k > 0[/latex]
Tada je
[latex]x_k := (-1)^{2k-1}\frac{a_{2k-1}}{2k-1} + (-1)^{2k}\frac{a_{2k}}{2k} = \frac9{2k}-\frac1{2k-1} > \frac8{2k} = \frac4k[/latex]
Ocito, jer sam zbrajao dva i dva susjedna i onda sve skupa, vrijedi:
[latex]\sum_n (-1)^n \frac{a_n}n = \sum_k x_k[/latex],
pa imamo (uz pretpostavku da suma reda postoji)
[latex]4\sum_k\frac1k < \sum_k x_k = \sum_n (-1)^n \frac{a_n}n[/latex],
pa ja nekako zakljucujem da taj red malo divergira. :D
Grijesim li negdje? :-k
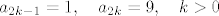
Tada je
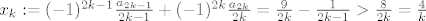
Ocito, jer sam zbrajao dva i dva susjedna i onda sve skupa, vrijedi:
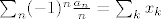 , ,
pa imamo (uz pretpostavku da suma reda postoji)
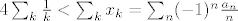 , ,
pa ja nekako zakljucujem da taj red malo divergira. 
Grijesim li negdje? 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 3:32 sub, 27. 9. 2008 Naslov: Postano: 3:32 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="vsego"][latex]a_{2k-1} = 1, \quad a_{2k} = 9, \quad k > 0[/latex][/quote]
Ja sam shvatio da se traži da niz sadrži sve članove {1,2,...,9} :-k ?
[quote][latex]\frac9{2k}-\frac1{2k-1} > \frac8{2k} = \frac4k[/latex][/quote]
Ako se uvrsti npr. k=10, tada je 9/20 - 1/19 = 0.397 što nije veće od 4/10=0.4 :)
| vsego (napisa): | 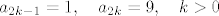 |
Ja sam shvatio da se traži da niz sadrži sve članove {1,2,...,9}  ? ?
| Citat: | 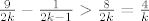 |
Ako se uvrsti npr. k=10, tada je 9/20 - 1/19 = 0.397 što nije veće od 4/10=0.4 
_________________
The Dude Abides
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 4:18 sub, 27. 9. 2008 Naslov: Postano: 4:18 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="goranm"][quote="vsego"][latex]a_{2k-1} = 1, \quad a_{2k} = 9, \quad k > 0[/latex][/quote]
Ja sam shvatio da se traži da niz sadrži sve članove {1,2,...,9} :-k ?[/quote]
Ja nisam, no to je nebitno, jer se rijesi preko prvih 9 elemenata niza, a oni su za konvergenciju reda nebitni. ;) Cak i da zelis iskoristiti sve brojeve "jednako mnogo puta", dalo bi se nastimati jako slicno ovom mom (samo ne bi uzimao 2 uzastopna clana niza, nego njih 18[i][/i]). :)
[quote="goranm"][quote="vsego"][latex]\frac9{2k}-\frac1{2k-1} > \frac8{2k} = \frac4k[/latex][/quote]
Ako se uvrsti npr. k=10, tada je 9/20 - 1/19 = 0.397 što nije veće od 4/10=0.4 :)[/quote]
Of course, silly me. :oops: No, za sve [latex]k \geq 1[/latex] je
[latex]\frac9{2k}-\frac1{2k-1} > \frac2{2k} = \frac1k[/latex]
(raspise se, trazis k i dobijes k > 7/12 ili tako nesto)
Poanta ostaje: suma, kad bi postojala, mora biti veca od [latex]\sum_k \frac1k[/latex] za sto znamo da bjezi u beskonacnost. 8)
| goranm (napisa): | | vsego (napisa): | 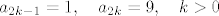 |
Ja sam shvatio da se traži da niz sadrži sve članove {1,2,...,9}  ? ? |
Ja nisam, no to je nebitno, jer se rijesi preko prvih 9 elemenata niza, a oni su za konvergenciju reda nebitni.  Cak i da zelis iskoristiti sve brojeve "jednako mnogo puta", dalo bi se nastimati jako slicno ovom mom (samo ne bi uzimao 2 uzastopna clana niza, nego njih 18). Cak i da zelis iskoristiti sve brojeve "jednako mnogo puta", dalo bi se nastimati jako slicno ovom mom (samo ne bi uzimao 2 uzastopna clana niza, nego njih 18). 
| goranm (napisa): | | vsego (napisa): | 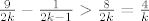 |
Ako se uvrsti npr. k=10, tada je 9/20 - 1/19 = 0.397 što nije veće od 4/10=0.4  |
Of course, silly me.  No, za sve No, za sve  je je
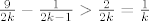
(raspise se, trazis k i dobijes k > 7/12 ili tako nesto)
Poanta ostaje: suma, kad bi postojala, mora biti veca od 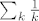 za sto znamo da bjezi u beskonacnost. za sto znamo da bjezi u beskonacnost. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
 Postano: 9:48 sub, 27. 9. 2008 Naslov: Postano: 9:48 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="vsego"][latex]a_{2k-1} = 1, \quad a_{2k} = 9, \quad k > 0[/latex]
Tada je
[latex]x_k := (-1)^{2k-1}\frac{a_{2k-1}}{2k-1} + (-1)^{2k}\frac{a_{2k}}{2k} = \frac9{2k}-\frac1{2k-1} > \frac8{2k} = \frac4k[/latex]
Ocito, jer sam zbrajao dva i dva susjedna i onda sve skupa, vrijedi:
[latex]\sum_n (-1)^n \frac{a_n}n = \sum_k x_k[/latex],
pa imamo (uz pretpostavku da suma reda postoji)
[latex]4\sum_k\frac1k < \sum_k x_k = \sum_n (-1)^n \frac{a_n}n[/latex],
pa ja nekako zakljucujem da taj red malo divergira. :D
Grijesim li negdje? :-k[/quote]
Ne znam. Pišeš gore da si zbrajao dva i dva susjedna i onda sve skupa. To znači da si umetao zagrade u red. Nisam siguran da li to smiješ činiti kod uvjetno konvergentnih redova(u slučaju da je red uvjetno konvergentan)?
Ispravi me ako griješim?
[size=9][color=#999999]Added after 13 minutes:[/color][/size]
[quote="StateOfConsciousness"][quote="vsego"][latex]a_{2k-1} = 1, \quad a_{2k} = 9, \quad k > 0[/latex]
Tada je
[latex]x_k := (-1)^{2k-1}\frac{a_{2k-1}}{2k-1} + (-1)^{2k}\frac{a_{2k}}{2k} = \frac9{2k}-\frac1{2k-1} > \frac8{2k} = \frac4k[/latex]
Ocito, jer sam zbrajao dva i dva susjedna i onda sve skupa, vrijedi:
[latex]\sum_n (-1)^n \frac{a_n}n = \sum_k x_k[/latex],
pa imamo (uz pretpostavku da suma reda postoji)
[latex]4\sum_k\frac1k < \sum_k x_k = \sum_n (-1)^n \frac{a_n}n[/latex],
pa ja nekako zakljucujem da taj red malo divergira. :D
Grijesim li negdje? :-k[/quote]
Ne znam. Pišeš gore da si zbrajao dva i dva susjedna i onda sve skupa. To znači da si umetao zagrade u red. Nisam siguran da li to smiješ činiti kod uvjetno konvergentnih redova(u slučaju da je red uvjetno konvergentan)?
Ispravi me ako griješim?[/quote]
U slučaju da se smiju umetati zagrade pokazao si da svi redovi gornjeg oblika nisu konvergentni. Sada me zanima možeš li naći(ti ili netko drugi) primjer reda ili klase redova kojem je opći član gore napisanog oblika a koji konvergiraju i pritom apsolutne vrijednosti članova niza ne padaju monotono(tj.ne može se primijeniti Leibnitzov kriterij da se utvrdi konvergencija)?
[size=9][color=#999999]Added after 7 minutes:[/color][/size]
[quote="StateOfConsciousness"][quote="vsego"][latex]a_{2k-1} = 1, \quad a_{2k} = 9, \quad k > 0[/latex]
Tada je
[latex]x_k := (-1)^{2k-1}\frac{a_{2k-1}}{2k-1} + (-1)^{2k}\frac{a_{2k}}{2k} = \frac9{2k}-\frac1{2k-1} > \frac8{2k} = \frac4k[/latex]
Ocito, jer sam zbrajao dva i dva susjedna i onda sve skupa, vrijedi:
[latex]\sum_n (-1)^n \frac{a_n}n = \sum_k x_k[/latex],
pa imamo (uz pretpostavku da suma reda postoji)
[latex]4\sum_k\frac1k < \sum_k x_k = \sum_n (-1)^n \frac{a_n}n[/latex],
pa ja nekako zakljucujem da taj red malo divergira. :D
Grijesim li negdje? :-k[/quote]
Ne znam. Pišeš gore da si zbrajao dva i dva susjedna i onda sve skupa. To znači da si umetao zagrade u red. Nisam siguran da li to smiješ činiti kod uvjetno konvergentnih redova(u slučaju da je red uvjetno konvergentan)?
Ispravi me ako griješim?
[size=9][color=#999999]Added after 13 minutes:[/color][/size]
[quote="StateOfConsciousness"][quote="vsego"][latex]a_{2k-1} = 1, \quad a_{2k} = 9, \quad k > 0[/latex]
Tada je
[latex]x_k := (-1)^{2k-1}\frac{a_{2k-1}}{2k-1} + (-1)^{2k}\frac{a_{2k}}{2k} = \frac9{2k}-\frac1{2k-1} > \frac8{2k} = \frac4k[/latex]
Ocito, jer sam zbrajao dva i dva susjedna i onda sve skupa, vrijedi:
[latex]\sum_n (-1)^n \frac{a_n}n = \sum_k x_k[/latex],
pa imamo (uz pretpostavku da suma reda postoji)
[latex]4\sum_k\frac1k < \sum_k x_k = \sum_n (-1)^n \frac{a_n}n[/latex],
pa ja nekako zakljucujem da taj red malo divergira. :D
Grijesim li negdje? :-k[/quote]
Ne znam. Pišeš gore da si zbrajao dva i dva susjedna i onda sve skupa. To znači da si umetao zagrade u red. Nisam siguran da li to smiješ činiti kod uvjetno konvergentnih redova(u slučaju da je red uvjetno konvergentan)?
Ispravi me ako griješim?[/quote]
U slučaju da se smiju umetati zagrade pokazao si da svi redovi gornjeg oblika nisu konvergentni. Sada me zanima možeš li naći(ti ili netko drugi) primjer reda ili klase redova kojem je opći član gore napisanog oblika a koji konvergiraju i pritom apsolutne vrijednosti članova niza ne padaju monotono(tj.ne može se primijeniti Leibnitzov kriterij da se utvrdi konvergencija)?[/quote]
Evo našao sam ja neke "trivijalne" primjere: Ako je a(n)=1 za sve osim eventualno konačno mnogo članova onda red konvergira. Zanimljivo bi bilo pronaći niz [b]a[/b] takav da on sadrži svaku od znamenaka 1,2,3,4,5,6,7,8,9 prebrojivo puta a da red pritom konvergira. Ne znam da li sve sve znamenke pojavljuju jednako često ako svaku od njih sadži prebrojivo mnogo puta?
| vsego (napisa): | 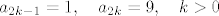
Tada je
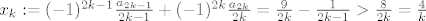
Ocito, jer sam zbrajao dva i dva susjedna i onda sve skupa, vrijedi:
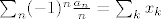 , ,
pa imamo (uz pretpostavku da suma reda postoji)
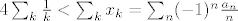 , ,
pa ja nekako zakljucujem da taj red malo divergira. 
Grijesim li negdje?  |
Ne znam. Pišeš gore da si zbrajao dva i dva susjedna i onda sve skupa. To znači da si umetao zagrade u red. Nisam siguran da li to smiješ činiti kod uvjetno konvergentnih redova(u slučaju da je red uvjetno konvergentan)?
Ispravi me ako griješim?
Added after 13 minutes:
| StateOfConsciousness (napisa): | | vsego (napisa): | 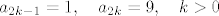
Tada je
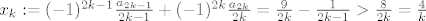
Ocito, jer sam zbrajao dva i dva susjedna i onda sve skupa, vrijedi:
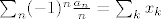 , ,
pa imamo (uz pretpostavku da suma reda postoji)
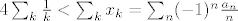 , ,
pa ja nekako zakljucujem da taj red malo divergira. 
Grijesim li negdje?  |
Ne znam. Pišeš gore da si zbrajao dva i dva susjedna i onda sve skupa. To znači da si umetao zagrade u red. Nisam siguran da li to smiješ činiti kod uvjetno konvergentnih redova(u slučaju da je red uvjetno konvergentan)?
Ispravi me ako griješim? |
U slučaju da se smiju umetati zagrade pokazao si da svi redovi gornjeg oblika nisu konvergentni. Sada me zanima možeš li naći(ti ili netko drugi) primjer reda ili klase redova kojem je opći član gore napisanog oblika a koji konvergiraju i pritom apsolutne vrijednosti članova niza ne padaju monotono(tj.ne može se primijeniti Leibnitzov kriterij da se utvrdi konvergencija)?
Added after 7 minutes:
| StateOfConsciousness (napisa): | | vsego (napisa): | 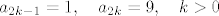
Tada je
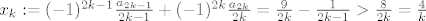
Ocito, jer sam zbrajao dva i dva susjedna i onda sve skupa, vrijedi:
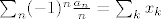 , ,
pa imamo (uz pretpostavku da suma reda postoji)
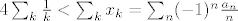 , ,
pa ja nekako zakljucujem da taj red malo divergira. 
Grijesim li negdje?  |
Ne znam. Pišeš gore da si zbrajao dva i dva susjedna i onda sve skupa. To znači da si umetao zagrade u red. Nisam siguran da li to smiješ činiti kod uvjetno konvergentnih redova(u slučaju da je red uvjetno konvergentan)?
Ispravi me ako griješim?
Added after 13 minutes:
| StateOfConsciousness (napisa): | | vsego (napisa): | 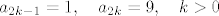
Tada je
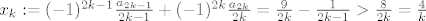
Ocito, jer sam zbrajao dva i dva susjedna i onda sve skupa, vrijedi:
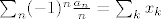 , ,
pa imamo (uz pretpostavku da suma reda postoji)
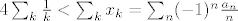 , ,
pa ja nekako zakljucujem da taj red malo divergira. 
Grijesim li negdje?  |
Ne znam. Pišeš gore da si zbrajao dva i dva susjedna i onda sve skupa. To znači da si umetao zagrade u red. Nisam siguran da li to smiješ činiti kod uvjetno konvergentnih redova(u slučaju da je red uvjetno konvergentan)?
Ispravi me ako griješim? |
U slučaju da se smiju umetati zagrade pokazao si da svi redovi gornjeg oblika nisu konvergentni. Sada me zanima možeš li naći(ti ili netko drugi) primjer reda ili klase redova kojem je opći član gore napisanog oblika a koji konvergiraju i pritom apsolutne vrijednosti članova niza ne padaju monotono(tj.ne može se primijeniti Leibnitzov kriterij da se utvrdi konvergencija)? |
Evo našao sam ja neke "trivijalne" primjere: Ako je a(n)=1 za sve osim eventualno konačno mnogo članova onda red konvergira. Zanimljivo bi bilo pronaći niz a takav da on sadrži svaku od znamenaka 1,2,3,4,5,6,7,8,9 prebrojivo puta a da red pritom konvergira. Ne znam da li sve sve znamenke pojavljuju jednako često ako svaku od njih sadži prebrojivo mnogo puta?
_________________
Look at every path closely and deliberately. Try it as many times as you think necessary. Then ask yourself,
and yourself alone, one question . . . Does this path have a heart? If it does, the path is good; if it doesn’t it is of no use.
Carlos Castaneda, The Teachings of Don juan
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 14:11 sub, 27. 9. 2008 Naslov: Postano: 14:11 sub, 27. 9. 2008 Naslov: |
    |
|
|
Zagrade, ako se dobro sjecam (a i ima mi smisla), smijes ubacivati. :) Ono sto ne smijes je permutirati (dakle, imas asocijativnost, ali ne i opcenitu komutativnost). 8)
"Jednako cesto" znaci da imas bijekciju izmedju indeksa na kojima je svaki od brojeva, a "prebrojivo" znaci "bijektivno s N", pa je odgovor na tvoje zadnje pitanje pozitivan. :)
Zagrade, ako se dobro sjecam (a i ima mi smisla), smijes ubacivati.  Ono sto ne smijes je permutirati (dakle, imas asocijativnost, ali ne i opcenitu komutativnost). Ono sto ne smijes je permutirati (dakle, imas asocijativnost, ali ne i opcenitu komutativnost). 
"Jednako cesto" znaci da imas bijekciju izmedju indeksa na kojima je svaki od brojeva, a "prebrojivo" znaci "bijektivno s N", pa je odgovor na tvoje zadnje pitanje pozitivan. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
 Postano: 14:28 sub, 27. 9. 2008 Naslov: Postano: 14:28 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="vsego"]Zagrade, ako se dobro sjecam (a i ima mi smisla), smijes ubacivati. :) Ono sto ne smijes je permutirati (dakle, imas asocijativnost, ali ne i opcenitu komutativnost). 8)
"Jednako cesto" znaci da imas bijekciju izmedju indeksa na kojima je svaki od brojeva, a "prebrojivo" znaci "bijektivno s N", pa je odgovor na tvoje zadnje pitanje pozitivan. :)[/quote]
Jesi uspio pronaći niz [b]a[/b] takav da on svaku od znamenki 1,2,3,4,5,6,7,8,9 sadrži prebrojivo mnogo puta a da je red kojem je opći član ((-1)^n)a(n)/n konvergentan?
Pokušaj. Ako ti(ili netko drugi) u kratkom roku ne uspiješ onda budem postavio jednu novu slutnju koju sam smislio a koja je, kako mi se čini, lakše rješiva od utvrđivanja tog da li određena klasa redova konvergira k iracionalnom broju.
P.S. Hvala na trudu.
| vsego (napisa): | Zagrade, ako se dobro sjecam (a i ima mi smisla), smijes ubacivati.  Ono sto ne smijes je permutirati (dakle, imas asocijativnost, ali ne i opcenitu komutativnost). Ono sto ne smijes je permutirati (dakle, imas asocijativnost, ali ne i opcenitu komutativnost). 
"Jednako cesto" znaci da imas bijekciju izmedju indeksa na kojima je svaki od brojeva, a "prebrojivo" znaci "bijektivno s N", pa je odgovor na tvoje zadnje pitanje pozitivan.  |
Jesi uspio pronaći niz a takav da on svaku od znamenki 1,2,3,4,5,6,7,8,9 sadrži prebrojivo mnogo puta a da je red kojem je opći član ((-1)^n)a(n)/n konvergentan?
Pokušaj. Ako ti(ili netko drugi) u kratkom roku ne uspiješ onda budem postavio jednu novu slutnju koju sam smislio a koja je, kako mi se čini, lakše rješiva od utvrđivanja tog da li određena klasa redova konvergira k iracionalnom broju.
P.S. Hvala na trudu.
_________________
Look at every path closely and deliberately. Try it as many times as you think necessary. Then ask yourself,
and yourself alone, one question . . . Does this path have a heart? If it does, the path is good; if it doesn’t it is of no use.
Carlos Castaneda, The Teachings of Don juan
|
|
| [Vrh] |
|
|









