| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
237115
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
|
| [Vrh] |
|
237115
Gost
|
 Postano: 18:57 sub, 27. 9. 2008 Naslov: Postano: 18:57 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="goranm"][quote="237115"]Je,je znam ja.Iracionalna je.[/quote]
Može li se dokaz negdje pročitati? :)[/quote]
Nisam ga još zgotovio u "čisto" :DMatematički dokazi su često vraška stvar. ..Ali posve sam siguran da je to iracionalno.
Kad imamo već u samom algoritmu za računanje uključen ln(n) ,a za sve prirodne n>1 ,a to je uvijek "debela" iracionalnost,nema šanse, ni na prvi pogled da u limesu E-M konstanta postane racionalna.To treba naravno striktno dokazati.Treba znati dovoljno ubrzati konvergenciju i neke sitnice oko broja [i]e[/i],čemu (zvučat će nevjerojatno) dosad nije posvećena dovoljna pažnja!
[quote="StateOfConsciousness"]
Ja mu ne vjerujem. Vjerujem da Matematika općenito još uvijek nije na toj razini da bi dokazala iracionalnost E-M konstante.[/quote]
Ne trebaš ništa vjerovati :)
Nisam rekao da znam jeli dokazano,nego da znam da je iracionalno.
Vjerujem da je matematika jeste općenito (odavno) na toj razini da bi dokazala dotičnu iracionalnost,ali matematičari su igrom slučaja propustili pohvatati prave konce da iznjedre dokaz.To će biti kratak dokaz.Vjerujem ne duži od onoga za [latex]\pi[/latex].
| goranm (napisa): | | 237115 (napisa): | | Je,je znam ja.Iracionalna je. |
Može li se dokaz negdje pročitati?  |
Nisam ga još zgotovio u "čisto" :DMatematički dokazi su često vraška stvar. ..Ali posve sam siguran da je to iracionalno.
Kad imamo već u samom algoritmu za računanje uključen ln(n) ,a za sve prirodne n>1 ,a to je uvijek "debela" iracionalnost,nema šanse, ni na prvi pogled da u limesu E-M konstanta postane racionalna.To treba naravno striktno dokazati.Treba znati dovoljno ubrzati konvergenciju i neke sitnice oko broja e,čemu (zvučat će nevjerojatno) dosad nije posvećena dovoljna pažnja!
| StateOfConsciousness (napisa): |
Ja mu ne vjerujem. Vjerujem da Matematika općenito još uvijek nije na toj razini da bi dokazala iracionalnost E-M konstante. |
Ne trebaš ništa vjerovati 
Nisam rekao da znam jeli dokazano,nego da znam da je iracionalno.
Vjerujem da je matematika jeste općenito (odavno) na toj razini da bi dokazala dotičnu iracionalnost,ali matematičari su igrom slučaja propustili pohvatati prave konce da iznjedre dokaz.To će biti kratak dokaz.Vjerujem ne duži od onoga za  . .
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
 Postano: 19:15 sub, 27. 9. 2008 Naslov: Postano: 19:15 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="237115"][quote="goranm"][quote="237115"]Je,je znam ja.Iracionalna je.[/quote]
Može li se dokaz negdje pročitati? :)[/quote]
Nisam ga još zgotovio u "čisto" :DMatematički dokazi su često vraška stvar. ..Ali posve sam siguran da je to iracionalno.
Kad imamo već u samom algoritmu za računanje uključen ln(n) ,a za sve prirodne n>1 ,a to je uvijek "debela" iracionalnost,nema šanse, ni na prvi pogled da u limesu E-M konstanta postane racionalna.To treba naravno striktno dokazati.Treba znati dovoljno ubrzati konvergenciju i neke sitnice oko broja [i]e[/i],čemu (zvučat će nevjerojatno) dosad nije posvećena dovoljna pažnja!
[quote="StateOfConsciousness"]
Ja mu ne vjerujem. Vjerujem da Matematika općenito još uvijek nije na toj razini da bi dokazala iracionalnost E-M konstante.[/quote]
Ne trebaš ništa vjerovati :)
Nisam rekao da znam jeli dokazano,nego da znam da je iracionalno.
Vjerujem da je matematika jeste općenito (odavno) na toj razini da bi dokazala dotičnu iracionalnost,ali matematičari su igrom slučaja propustili pohvatati prave konce da iznjedre dokaz.To će biti kratak dokaz.Vjerujem ne duži od onoga za [latex]\pi[/latex].[/quote]
Ja sam samo napisao da ne vjerujem da imaš dokaz. Ništa drugo. A ne vjerujem da će se dokazati da je iracionalan tako da se promatra limes niza n-> (1+ 1/2+1/3+...+1/n - ln(n)) već promatrajući neki red koji konvergira k E-M konstanti, kao što je onaj kojem je opći član, ako se ne varam ((-1)^n)(floor(ln(n)))/n. A najvjerojatnije će dokaz biti preko proučavanja tog kako se ponašaju periodi recipročnih brojeva prostih brojeva... Barem bih ja tim putem išao. No to ne mora značiti da je taj put ispravan. Ne mora značiti ništa.
| 237115 (napisa): | | goranm (napisa): | | 237115 (napisa): | | Je,je znam ja.Iracionalna je. |
Može li se dokaz negdje pročitati?  |
Nisam ga još zgotovio u "čisto" :DMatematički dokazi su često vraška stvar. ..Ali posve sam siguran da je to iracionalno.
Kad imamo već u samom algoritmu za računanje uključen ln(n) ,a za sve prirodne n>1 ,a to je uvijek "debela" iracionalnost,nema šanse, ni na prvi pogled da u limesu E-M konstanta postane racionalna.To treba naravno striktno dokazati.Treba znati dovoljno ubrzati konvergenciju i neke sitnice oko broja e,čemu (zvučat će nevjerojatno) dosad nije posvećena dovoljna pažnja!
| StateOfConsciousness (napisa): |
Ja mu ne vjerujem. Vjerujem da Matematika općenito još uvijek nije na toj razini da bi dokazala iracionalnost E-M konstante. |
Ne trebaš ništa vjerovati 
Nisam rekao da znam jeli dokazano,nego da znam da je iracionalno.
Vjerujem da je matematika jeste općenito (odavno) na toj razini da bi dokazala dotičnu iracionalnost,ali matematičari su igrom slučaja propustili pohvatati prave konce da iznjedre dokaz.To će biti kratak dokaz.Vjerujem ne duži od onoga za  . . |
Ja sam samo napisao da ne vjerujem da imaš dokaz. Ništa drugo. A ne vjerujem da će se dokazati da je iracionalan tako da se promatra limes niza n→ (1+ 1/2+1/3+...+1/n - ln(n)) već promatrajući neki red koji konvergira k E-M konstanti, kao što je onaj kojem je opći član, ako se ne varam ((-1)^n)(floor(ln(n)))/n. A najvjerojatnije će dokaz biti preko proučavanja tog kako se ponašaju periodi recipročnih brojeva prostih brojeva... Barem bih ja tim putem išao. No to ne mora značiti da je taj put ispravan. Ne mora značiti ništa.
_________________
Look at every path closely and deliberately. Try it as many times as you think necessary. Then ask yourself,
and yourself alone, one question . . . Does this path have a heart? If it does, the path is good; if it doesn’t it is of no use.
Carlos Castaneda, The Teachings of Don juan
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:42 sub, 27. 9. 2008 Naslov: Postano: 19:42 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="237115"]Nisam ga još zgotovio u "čisto" :DMatematički dokazi su često vraška stvar. ..Ali posve sam siguran da je to iracionalno.
Kad imamo već u samom algoritmu za računanje uključen ln(n) ,a za sve prirodne n>1 ,a to je uvijek "debela" iracionalnost,nema šanse, ni na prvi pogled da u limesu E-M konstanta postane racionalna.[/quote]
No tako možemo reći da nema šanse da je limes niza ((n+1)/n)^n iracionalan jer za sve prirodne n>1 to je "debela" racionalnost, što ne? :)
Sretno s dokazivanjem :)
| 237115 (napisa): | Nisam ga još zgotovio u "čisto" :DMatematički dokazi su često vraška stvar. ..Ali posve sam siguran da je to iracionalno.
Kad imamo već u samom algoritmu za računanje uključen ln(n) ,a za sve prirodne n>1 ,a to je uvijek "debela" iracionalnost,nema šanse, ni na prvi pogled da u limesu E-M konstanta postane racionalna. |
No tako možemo reći da nema šanse da je limes niza ((n+1)/n)^n iracionalan jer za sve prirodne n>1 to je "debela" racionalnost, što ne? 
Sretno s dokazivanjem 
_________________
The Dude Abides
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
 Postano: 20:00 sub, 27. 9. 2008 Naslov: Postano: 20:00 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="goranm"][quote="237115"]Nisam ga još zgotovio u "čisto" :DMatematički dokazi su često vraška stvar. ..Ali posve sam siguran da je to iracionalno.
Kad imamo već u samom algoritmu za računanje uključen ln(n) ,a za sve prirodne n>1 ,a to je uvijek "debela" iracionalnost,nema šanse, ni na prvi pogled da u limesu E-M konstanta postane racionalna.[/quote]
No tako možemo reći da nema šanse da je limes niza ((n+1)/n)^n iracionalan jer za sve prirodne n>1 to je "debela" racionalnost, što ne? :)
Sretno s dokazivanjem :)[/quote]
Da, moglo bi se tako reći. Nego, smislio sam jedan novi problem koji bi se možda mogao dokazati lakše nego iracionalnost E-M konstante a glasi:
Neka je a niz, a: [b]N[/b]->[b]N[/b] takav da vrijedi lim a(n)/n=0. Dokazati da je red kojem je opći član ((-1)^n)(a(n))/n konvergentan. Hmmmmm..... I nije tako lako. Što vi koji čitate ovaj post mislite? Lako?
| goranm (napisa): | | 237115 (napisa): | Nisam ga još zgotovio u "čisto" :DMatematički dokazi su često vraška stvar. ..Ali posve sam siguran da je to iracionalno.
Kad imamo već u samom algoritmu za računanje uključen ln(n) ,a za sve prirodne n>1 ,a to je uvijek "debela" iracionalnost,nema šanse, ni na prvi pogled da u limesu E-M konstanta postane racionalna. |
No tako možemo reći da nema šanse da je limes niza ((n+1)/n)^n iracionalan jer za sve prirodne n>1 to je "debela" racionalnost, što ne? 
Sretno s dokazivanjem  |
Da, moglo bi se tako reći. Nego, smislio sam jedan novi problem koji bi se možda mogao dokazati lakše nego iracionalnost E-M konstante a glasi:
Neka je a niz, a: N→N takav da vrijedi lim a(n)/n=0. Dokazati da je red kojem je opći član ((-1)^n)(a(n))/n konvergentan. Hmmmmm..... I nije tako lako. Što vi koji čitate ovaj post mislite? Lako?
_________________
Look at every path closely and deliberately. Try it as many times as you think necessary. Then ask yourself,
and yourself alone, one question . . . Does this path have a heart? If it does, the path is good; if it doesn’t it is of no use.
Carlos Castaneda, The Teachings of Don juan
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 20:15 sub, 27. 9. 2008 Naslov: Postano: 20:15 sub, 27. 9. 2008 Naslov: |
    |
|
|
Trivijalno: [latex]a_{2k-1} = 0, \quad a_{2k} = 1, \quad k > 0[/latex]
Ocito je
[latex]\lim_n \frac{a_n}n = 0[/latex]
i
[latex]\sum_n (-1)^n\frac{a_n}n = \sum_k \frac1k[/latex]
Dakle, "slutnja" ne vrijedi. 8)
Mozda da malo sam mozgas nad svojim "slutnjama", umjesto da napises ovdje sve sto ti padne na pamet i onda cekas da to netko iskrampa? :-k Meni je slucajno uletjelo sitno vremena, pa se igram ovim tvojim ocitostima, no nekako mi nema smisla. :? Valjda je poanta bavljenja matematikom sama matematika, a ne samo izbacivanje kojekakvih tvrdnji... valjda sa svrhom da nadjes zanimaciju matematicarima koji ne znaju cime bi se bavili. :P
Trivijalno: 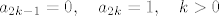
Ocito je
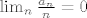
i
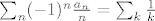
Dakle, "slutnja" ne vrijedi. 
Mozda da malo sam mozgas nad svojim "slutnjama", umjesto da napises ovdje sve sto ti padne na pamet i onda cekas da to netko iskrampa?  Meni je slucajno uletjelo sitno vremena, pa se igram ovim tvojim ocitostima, no nekako mi nema smisla. Meni je slucajno uletjelo sitno vremena, pa se igram ovim tvojim ocitostima, no nekako mi nema smisla.  Valjda je poanta bavljenja matematikom sama matematika, a ne samo izbacivanje kojekakvih tvrdnji... valjda sa svrhom da nadjes zanimaciju matematicarima koji ne znaju cime bi se bavili. Valjda je poanta bavljenja matematikom sama matematika, a ne samo izbacivanje kojekakvih tvrdnji... valjda sa svrhom da nadjes zanimaciju matematicarima koji ne znaju cime bi se bavili. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
 Postano: 20:24 sub, 27. 9. 2008 Naslov: Postano: 20:24 sub, 27. 9. 2008 Naslov: |
    |
|
|
[quote="vsego"]Trivijalno: [latex]a_{2k-1} = 0, \quad a_{2k} = 1, \quad k > 0[/latex]
Ocito je
[latex]\lim_n \frac{a_n}n = 0[/latex]
i
[latex]\sum_n (-1)^n\frac{a_n}n = \sum_k \frac1k[/latex]
Dakle, "slutnja" ne vrijedi. 8)
Mozda da malo sam mozgas nad svojim "slutnjama", umjesto da napises ovdje sve sto ti padne na pamet i onda cekas da to netko iskrampa? :-k Meni je slucajno uletjelo sitno vremena, pa se igram ovim tvojim ocitostima, no nekako mi nema smisla. :? Valjda je poanta bavljenja matematikom sama matematika, a ne samo izbacivanje kojekakvih tvrdnji... valjda sa svrhom da nadjes zanimaciju matematicarima koji ne znaju cime bi se bavili. :P[/quote]
Mudro zboriš. Naravno da je gornja slutnja trivijalna jer sam zaboravio ubaciti to da je niz [b]a[/b] strogo pozitivan i rastući. Jel sada trivijalna? Svaka čast ako ti je trivijalna. Meni nije,
| vsego (napisa): | Trivijalno: 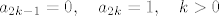
Ocito je
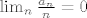
i
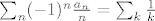
Dakle, "slutnja" ne vrijedi. 
Mozda da malo sam mozgas nad svojim "slutnjama", umjesto da napises ovdje sve sto ti padne na pamet i onda cekas da to netko iskrampa?  Meni je slucajno uletjelo sitno vremena, pa se igram ovim tvojim ocitostima, no nekako mi nema smisla. Meni je slucajno uletjelo sitno vremena, pa se igram ovim tvojim ocitostima, no nekako mi nema smisla.  Valjda je poanta bavljenja matematikom sama matematika, a ne samo izbacivanje kojekakvih tvrdnji... valjda sa svrhom da nadjes zanimaciju matematicarima koji ne znaju cime bi se bavili. Valjda je poanta bavljenja matematikom sama matematika, a ne samo izbacivanje kojekakvih tvrdnji... valjda sa svrhom da nadjes zanimaciju matematicarima koji ne znaju cime bi se bavili.  |
Mudro zboriš. Naravno da je gornja slutnja trivijalna jer sam zaboravio ubaciti to da je niz a strogo pozitivan i rastući. Jel sada trivijalna? Svaka čast ako ti je trivijalna. Meni nije,
_________________
Look at every path closely and deliberately. Try it as many times as you think necessary. Then ask yourself,
and yourself alone, one question . . . Does this path have a heart? If it does, the path is good; if it doesn’t it is of no use.
Carlos Castaneda, The Teachings of Don juan
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
|
| [Vrh] |
|
237115
Gost
|
 Postano: 10:01 ned, 28. 9. 2008 Naslov: Postano: 10:01 ned, 28. 9. 2008 Naslov: |
    |
|
|
[quote="goranm"]
No tako možemo reći da nema šanse da je limes niza ((n+1)/n)^n iracionalan jer za sve prirodne n>1 to je "debela" racionalnost, što ne? :)
[/quote]
Ne,ne možeš tako generalizirati.Točno da ovaj [i]e[/i]-ovski u raspisu ima svaku parcijalnu sumu racionalnu,ali konvergencija je tako brza da limes ne može biti racionalan.I kako se zapravo pokazuje da većina nizova definiranih u [latex]\mathbb{Q}[/latex],ako su konvergentni,bez obzira na brzinu konvergencije imaju limes u [latex]\mathbb{R}[/latex].Ali ako u nekom algoritmu racionalne članove zamijeniš sa iracionalnim ,limes tako dobivenog niza neće biti racionalan,nego će općenito padati u [latex]\mathbb{R}[/latex],i biti iracionalan (ili će dogoditi divergencija).To se dotiče i teorije skupova koja govori o različitom "bogatstvu" elementima skupova [latex]\mathbb{Q}[/latex] i [latex]\mathbb{R}[/latex].
Naravno ,da se ovo ne može iskoristiti u konkretnim dokazivanjima (i)racionalnosti ,ali je dodatni jak razlog zašto bi [latex]\gamma[/latex] trebala biti iracionalna konstanta.
[quote="goranm"]
Sretno s dokazivanjem :)[/quote]
A jok,to će morati pričekati.
Kao fizičara mnogo me više interesiraju Feigenbaumove konstante.Da se kojim čudom pokaže da nisu transcedentne (to se mislim neće dogoditi) ta stvar bi imala dalekosežne posljedice u teoriji kaosa i nelinearnih sistema.
| goranm (napisa): |
No tako možemo reći da nema šanse da je limes niza ((n+1)/n)^n iracionalan jer za sve prirodne n>1 to je "debela" racionalnost, što ne? 
|
Ne,ne možeš tako generalizirati.Točno da ovaj e-ovski u raspisu ima svaku parcijalnu sumu racionalnu,ali konvergencija je tako brza da limes ne može biti racionalan.I kako se zapravo pokazuje da većina nizova definiranih u 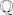 ,ako su konvergentni,bez obzira na brzinu konvergencije imaju limes u ,ako su konvergentni,bez obzira na brzinu konvergencije imaju limes u  .Ali ako u nekom algoritmu racionalne članove zamijeniš sa iracionalnim ,limes tako dobivenog niza neće biti racionalan,nego će općenito padati u .Ali ako u nekom algoritmu racionalne članove zamijeniš sa iracionalnim ,limes tako dobivenog niza neće biti racionalan,nego će općenito padati u  ,i biti iracionalan (ili će dogoditi divergencija).To se dotiče i teorije skupova koja govori o različitom "bogatstvu" elementima skupova ,i biti iracionalan (ili će dogoditi divergencija).To se dotiče i teorije skupova koja govori o različitom "bogatstvu" elementima skupova 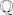 i i  . .
Naravno ,da se ovo ne može iskoristiti u konkretnim dokazivanjima (i)racionalnosti ,ali je dodatni jak razlog zašto bi 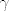 trebala biti iracionalna konstanta. trebala biti iracionalna konstanta.
| goranm (napisa): |
Sretno s dokazivanjem  |
A jok,to će morati pričekati.
Kao fizičara mnogo me više interesiraju Feigenbaumove konstante.Da se kojim čudom pokaže da nisu transcedentne (to se mislim neće dogoditi) ta stvar bi imala dalekosežne posljedice u teoriji kaosa i nelinearnih sistema.
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
StateOfConsciousness
Forumaš s poteškoćama u pisanju


Pridružen/a: 22. 07. 2008. (16:08:24)
Postovi: (8A)16
|
|
| [Vrh] |
|
|








