|
Uvedimo koordinatni sustav u ravnini takav da je vektor m jedinični vektor na osi x, tj m=i (ovo ne smanjuje općenitost). Dalje, ako je vektor j jedinični vektor na y-osi, tada je vektor n= i cos45° + j cos 45° = [latex]\frac{\sqrt{2}}{2}[/latex](i + j).
Sada lako dobivamo da je [latex]\overrightarrow{e} = \frac{4 - \sqrt{2}}{2} \overrightarrow{i} - \frac{\sqrt{2}}{2} \overrightarrow{j}[/latex] i [latex]\overrightarrow{f} = \frac{8 - 5\sqrt{2}}{2} \overrightarrow{i} - \frac{5\sqrt{2}}{2} \overrightarrow{j}[/latex].
Dalje, lako nalazimo da je [latex]\left|\overrightarrow{e}\right| = \sqrt{5 - 2\sqrt{2}}[/latex], [latex]\left|\overrightarrow{f}\right| = \sqrt{41 - 20\sqrt{2}}[/latex] i [latex]\measuredangle{\left(\overrightarrow{e},\, \overrightarrow{f}\right)} \approx 53^{\circ} 50' 27'' [/latex].
Dalje, površina paralelograma s dijagonalama e i f i kutem među njima x je dana s P=(1/2)*e*f*sin(x). Stranice paralelograma lako nalazimo (dijagonale se raspolovaljvaju, pa primjenimo kosinusov poučak na polovice dijagonala i kut x te dobijemo jednu stranicu, a primjenimo li ga na polovice dijagonala i kut pi-x dobivamo drugu stranicu).
Uvedimo koordinatni sustav u ravnini takav da je vektor m jedinični vektor na osi x, tj m=i (ovo ne smanjuje općenitost). Dalje, ako je vektor j jedinični vektor na y-osi, tada je vektor n= i cos45° + j cos 45° = 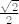 (i + j). (i + j).
Sada lako dobivamo da je 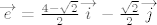 i i 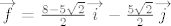 . .
Dalje, lako nalazimo da je 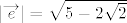 , , 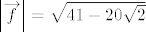 i i 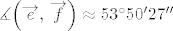 . .
Dalje, površina paralelograma s dijagonalama e i f i kutem među njima x je dana s P=(1/2)*e*f*sin(x). Stranice paralelograma lako nalazimo (dijagonale se raspolovaljvaju, pa primjenimo kosinusov poučak na polovice dijagonala i kut x te dobijemo jednu stranicu, a primjenimo li ga na polovice dijagonala i kut pi-x dobivamo drugu stranicu).
|





