| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
blabla
Forumaš(ica)

Pridružen/a: 02. 09. 2007. (15:39:56)
Postovi: (13)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 1:09 pon, 3. 11. 2008 Naslov: Postano: 1:09 pon, 3. 11. 2008 Naslov: |
    |
|
|
[quote="gaston"]evo, ja bih upao sa jednim drugim pitanjem, vezanim za zadatak 9.c)
neka je dan skup [latex]A[/latex] od [latex]n[/latex] elemenata. odredite koliko ima rastucih funkcija [latex]f:A\rightarrow A[/latex]
e sad, pretpostavljam da smijemo, bez smanjenja opcenitosti, uzeti [latex]A=\{1, 2,...,n\}[/latex], pa ce za svaku rastucu funkciju [latex]f:A\rightarrow A[/latex] vrijediti
[latex]i<j \Rightarrow f(i) \leq f(j)[/latex], pri cemu su [latex]i,j \in \{1, 2,...,n\}[/latex]
vidljivo je naprimjer da ako je, npr. [latex]f(2)=5[/latex], onda je nuzno [latex]f(3), f(4),...f(n) \in \{5,...,n\}[/latex],
odnosno [latex](f(i)=k) \Rightarrow f(j) \geq k[/latex], za [latex](i<j \leq n)[/latex]
ali ne znam kako ovo svojstvo icemu pomaze.
nemam pojma kako prebrojati sve rastuce funkcije sa [latex]A[/latex] u [latex]A[/latex] i bio bih izuzetno zahvalan na svakoj pomoci :D[/quote]
[quote="krcko"]
Nije bas jednostavno. Probaj prvo prebrojati strogo rastuce funkcije, laske je. Vise onako za zagrijavanje (nije od velike koristi za tvoj zadatak Smile )
Za rastuce funkcije treba pogledati prirast u svakoj tocki: f(i)-f(i-1). Moze se napraviti bijekcija s necim sto se moze prebrojati pomocu "kuglica i stapica".
Sad sam primijetio da su domena i kodomena isti skup pa su strogo rastuce funkcije trivijala. Zadatak se inace moze rijesiti za f:{1,..,m}->{1,..,n}.[/quote]
pa ja sam to zamislio onda kao n jednakih kuglica i n kutija ( n - 1 ) štapića i gledao sve moguce rasporede, s tim da svaka "kutija" ima svoj redni broj i kada bi rasporedio kuglice po kutijama, u prvoj kutiji gdje bih našao kuglice( recimo k - ta kutija, s njih recimo l kuglica ), to bi mi znacilo da je f(1) = k, f(2) = k,..., f(l) = k, dalje analogno...
pa bi mi broj rastucih funkcija bio jednak broju razmjestaja n kuglica u n kutija: (2*n - 1 povrh n) (provjerio sam za n = 2 i n = 3 i nadam se da nije bilo samo slucajno točno)
| gaston (napisa): | evo, ja bih upao sa jednim drugim pitanjem, vezanim za zadatak 9.c)
neka je dan skup  od od  elemenata. odredite koliko ima rastucih funkcija elemenata. odredite koliko ima rastucih funkcija 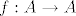
e sad, pretpostavljam da smijemo, bez smanjenja opcenitosti, uzeti 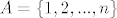 , pa ce za svaku rastucu funkciju , pa ce za svaku rastucu funkciju 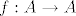 vrijediti vrijediti
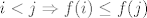 , pri cemu su , pri cemu su 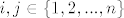
vidljivo je naprimjer da ako je, npr. 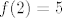 , onda je nuzno , onda je nuzno 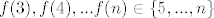 , ,
odnosno 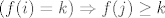 , za , za 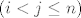
ali ne znam kako ovo svojstvo icemu pomaze.
nemam pojma kako prebrojati sve rastuce funkcije sa  u u  i bio bih izuzetno zahvalan na svakoj pomoci i bio bih izuzetno zahvalan na svakoj pomoci  |
| krcko (napisa): |
Nije bas jednostavno. Probaj prvo prebrojati strogo rastuce funkcije, laske je. Vise onako za zagrijavanje (nije od velike koristi za tvoj zadatak Smile )
Za rastuce funkcije treba pogledati prirast u svakoj tocki: f(i)-f(i-1). Moze se napraviti bijekcija s necim sto se moze prebrojati pomocu "kuglica i stapica".
Sad sam primijetio da su domena i kodomena isti skup pa su strogo rastuce funkcije trivijala. Zadatak se inace moze rijesiti za f:{1,..,m}→{1,..,n}. |
pa ja sam to zamislio onda kao n jednakih kuglica i n kutija ( n - 1 ) štapića i gledao sve moguce rasporede, s tim da svaka "kutija" ima svoj redni broj i kada bi rasporedio kuglice po kutijama, u prvoj kutiji gdje bih našao kuglice( recimo k - ta kutija, s njih recimo l kuglica ), to bi mi znacilo da je f(1) = k, f(2) = k,..., f(l) = k, dalje analogno...
pa bi mi broj rastucih funkcija bio jednak broju razmjestaja n kuglica u n kutija: (2*n - 1 povrh n) (provjerio sam za n = 2 i n = 3 i nadam se da nije bilo samo slucajno točno)
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 10:31 pon, 3. 11. 2008 Naslov: Postano: 10:31 pon, 3. 11. 2008 Naslov: |
    |
|
|
Mislim da je rezultat tocan, ali ne svidja mi se kako si objasnio bijekciju izmedju funkcija i rasporeda kuglica:
[quote="Cobs"]svaka "kutija" ima svoj redni broj i kada bi rasporedio kuglice po kutijama, u prvoj kutiji gdje bih našao kuglice( recimo k - ta kutija, s njih recimo l kuglica ), to bi mi znacilo da je f(1) = k, f(2) = k,..., f(l) = k, dalje analogno...[/quote]
Trebalo bi napisati:
1. kako tocno funkcijama pridruzujes rasporede kuglica
2. kako rasporedima kuglica pridruzujes funkcije (ovo gore nije dobro)
3. objasniti zasto su ta dva pridruzivanja medjusobno inverzna
Onda se mozes pozvati na formulu za kombinacije s ponavljanjem koju smo izveli na predavanjima.
Mislim da je rezultat tocan, ali ne svidja mi se kako si objasnio bijekciju izmedju funkcija i rasporeda kuglica:
| Cobs (napisa): | | svaka "kutija" ima svoj redni broj i kada bi rasporedio kuglice po kutijama, u prvoj kutiji gdje bih našao kuglice( recimo k - ta kutija, s njih recimo l kuglica ), to bi mi znacilo da je f(1) = k, f(2) = k,..., f(l) = k, dalje analogno... |
Trebalo bi napisati:
1. kako tocno funkcijama pridruzujes rasporede kuglica
2. kako rasporedima kuglica pridruzujes funkcije (ovo gore nije dobro)
3. objasniti zasto su ta dva pridruzivanja medjusobno inverzna
Onda se mozes pozvati na formulu za kombinacije s ponavljanjem koju smo izveli na predavanjima.
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
Vila Zvončica
Forumaš(ica)

Pridružen/a: 31. 01. 2008. (18:51:58)
Postovi: (17)16
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 10:45 uto, 4. 11. 2008 Naslov: Postano: 10:45 uto, 4. 11. 2008 Naslov: |
    |
|
|
[quote="sunny"]evo moja rjesenja od 5. :
a) (39 povrh 9)
b) 30^10
c) 30!/20!
d) .... isto kao a)
e)
f) (30*29*28)^10
g) (30 povrh 3)*(27 povrh 3)*...*(3 povrh 3)
da li je to tocno?
:)[/quote]
pa ja sam u:
(a) dobio 10^30 - nije nuzno da svi dobe zadatak, ali svaki zadatak mora dobiti točno jedan student ( u biti prvi zadatak mozes dati svoj desetorici, isto tako i drugi,..pa sve do 30. na taj nacin nije bilo nuzno da svaki dobije zadatak, ali svaki zadatak je podijeljen točno jednom studentu)
(b) nam je isti
(c) nam je isti
(d) ???
ako si shvatila što se u biti traži u (a) i ak vidis što se traži u (d) vidjet ćeš da ta dva baš i nemaju smisla(pročitaj postove od prije), tak da u biti rjesnje može biti to sto si stavila, ali je pitanje da li tu uopće ima rjesenja
(e)(30 povrh 3)*(27 povrh 3)*...*(3 povrh 3)
(f)(30 povrh 3)^10 - ti si stavila 30*29*28 cime biras tri zadatka od 30, ali si brojala previse puta ( isto ti je ako prvo biras 1.zad, pa recimo 5., pa recimo 25. ili ako biras prvo 25, pa 1. pa 5., a u tvojem je rjesenju to kao razlicito)
(g)(30 povrh 3)*(27 povrh 3)*...*(3 povrh 3)*10! - u (e) i (g) prvi dio rjesenja je isti grupiras zadatke u 10 grupa po tri bez da smijes ponavljati zadatke, samo sto si ti u (e) zadatku djelila sve te zadatke recimo po redu, a u (f) studenti sami biraju, pa 1. moze birati između 10grupa, drugi između 9 itd., zato ide *10!
rjesenja nisu nužno točna, ali sam usporedio sa ljudima iz svoje grupe i većina je tak imala, pa sad...
ak ti jos uvjek nekaj nije jasno, reci pa cu probati detaljnije objasnit
| sunny (napisa): | evo moja rjesenja od 5. :
a) (39 povrh 9)
b) 30^10
c) 30!/20!
d) .... isto kao a)
e)
f) (30*29*2 ^10 ^10
g) (30 povrh 3)*(27 povrh 3)*...*(3 povrh 3)
da li je to tocno?
 |
pa ja sam u:
(a) dobio 10^30 - nije nuzno da svi dobe zadatak, ali svaki zadatak mora dobiti točno jedan student ( u biti prvi zadatak mozes dati svoj desetorici, isto tako i drugi,..pa sve do 30. na taj nacin nije bilo nuzno da svaki dobije zadatak, ali svaki zadatak je podijeljen točno jednom studentu)
(b) nam je isti
(c) nam je isti
(d) ???
ako si shvatila što se u biti traži u (a) i ak vidis što se traži u (d) vidjet ćeš da ta dva baš i nemaju smisla(pročitaj postove od prije), tak da u biti rjesnje može biti to sto si stavila, ali je pitanje da li tu uopće ima rjesenja
(e)(30 povrh 3)*(27 povrh 3)*...*(3 povrh 3)
(f)(30 povrh 3)^10 - ti si stavila 30*29*28 cime biras tri zadatka od 30, ali si brojala previse puta ( isto ti je ako prvo biras 1.zad, pa recimo 5., pa recimo 25. ili ako biras prvo 25, pa 1. pa 5., a u tvojem je rjesenju to kao razlicito)
(g)(30 povrh 3)*(27 povrh 3)*...*(3 povrh 3)*10! - u (e) i (g) prvi dio rjesenja je isti grupiras zadatke u 10 grupa po tri bez da smijes ponavljati zadatke, samo sto si ti u (e) zadatku djelila sve te zadatke recimo po redu, a u (f) studenti sami biraju, pa 1. moze birati između 10grupa, drugi između 9 itd., zato ide *10!
rjesenja nisu nužno točna, ali sam usporedio sa ljudima iz svoje grupe i većina je tak imala, pa sad...
ak ti jos uvjek nekaj nije jasno, reci pa cu probati detaljnije objasnit
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
 Postano: 12:08 uto, 4. 11. 2008 Naslov: Postano: 12:08 uto, 4. 11. 2008 Naslov: |
    |
|
|
[quote="Cobs"]
(a) dobio 10^30 - nije nuzno da svi dobe zadatak, ali svaki zadatak mora dobiti točno jedan student ( u biti prvi zadatak mozes dati svoj desetorici, isto tako i drugi,..pa sve do 30. na taj nacin nije bilo nuzno da svaki dobije zadatak, ali svaki zadatak je podijeljen točno jednom studentu)
[/quote]
da... sad mi je ovaj jasniji
ja sam to radila na sljedeci nacin i imalo mi je smisla, samo mi je donekle smisla :
neka nam z[i] oznacava broj zadataka koji je dobio i-ti student
z[1]+z[2]+....+z[10]=30 i onda mi je k=10, n=30 i onda to rijesim pomocu one formule za kombinacije s ponavljanjem... samo me zbunjivalo to sto su zadatci razliciti... dakle ipak ne mogu tako jer je raspored zadataka bitan
[quote="Cobs"]
(f)(30 povrh 3)^10 - ti si stavila 30*29*28 cime biras tri zadatka od 30, ali si brojala previse puta ( isto ti je ako prvo biras 1.zad, pa recimo 5., pa recimo 25. ili ako biras prvo 25, pa 1. pa 5., a u tvojem je rjesenju to kao razlicito)
[/quote]
mene uzasno zbunjuje kad je raspored bitan, a kad nije... posto na pocetku zadatka pise da su zadatci razliciti, mislila sam da je raspored svagdje bitan (dakle da mi zbog toga rjesenje pod a) ne valja). Kako da znam da mi nije bitno koji zadatak je student izabrao kao prvi, koji kao drugi, a koji kao treci?
Mozda ce ti se to ciniti totalno smijesno, ali meni to nikako nije jasno :(
Jer, po mojoj logici, ako pod f) raspored nije bitan, onda nije bitan ni raspored u onom pod a) jer mi je onda svejedno koji je poredak zadataka je kod prvog studenta, koji je poredak kod drugog studenta,... i onda mi taj pod a) valja.
I jos nesto... ako je opcenito bitan raspored u cijelom zadatku zasto onda u g) zadatku ne mnozimo rjesenje sa 3!^10? (kao.. prvi u svakoj grupi mozemo izabrati na 3 nacina, drugi na 2 i treci na 1 i imamo 10 grupa).
Mislim da se iz prilozenog vidi da me diskretna poprilicno puno puno zbunjuje... tj. jedino me zbunjuje to sto ne znam prepoznati kad je raspored bitan, a kad nije?
i jos nesto... jel ne bih trebala u g) dijeliti sa 10! jer studenti sami biraju grupe... pa tako da mi je svejedno kakav ce mi raspored grupa biti... jer, po mome, da je raspored grupa bitan onda bi bilo napisano na koliko nacina mogu studenti izabrati zadatke grupirane u 10 grupa od po 3 zadatka...
a moguce da sam ja u totalnoj zabludi sto se tice svega :(
@ cobs & rafaelm : puno hvala :)
| Cobs (napisa): |
(a) dobio 10^30 - nije nuzno da svi dobe zadatak, ali svaki zadatak mora dobiti točno jedan student ( u biti prvi zadatak mozes dati svoj desetorici, isto tako i drugi,..pa sve do 30. na taj nacin nije bilo nuzno da svaki dobije zadatak, ali svaki zadatak je podijeljen točno jednom studentu)
|
da... sad mi je ovaj jasniji
ja sam to radila na sljedeci nacin i imalo mi je smisla, samo mi je donekle smisla :
neka nam z[i] oznacava broj zadataka koji je dobio i-ti student
z[1]+z[2]+....+z[10]=30 i onda mi je k=10, n=30 i onda to rijesim pomocu one formule za kombinacije s ponavljanjem... samo me zbunjivalo to sto su zadatci razliciti... dakle ipak ne mogu tako jer je raspored zadataka bitan
| Cobs (napisa): |
(f)(30 povrh 3)^10 - ti si stavila 30*29*28 cime biras tri zadatka od 30, ali si brojala previse puta ( isto ti je ako prvo biras 1.zad, pa recimo 5., pa recimo 25. ili ako biras prvo 25, pa 1. pa 5., a u tvojem je rjesenju to kao razlicito)
|
mene uzasno zbunjuje kad je raspored bitan, a kad nije... posto na pocetku zadatka pise da su zadatci razliciti, mislila sam da je raspored svagdje bitan (dakle da mi zbog toga rjesenje pod a) ne valja). Kako da znam da mi nije bitno koji zadatak je student izabrao kao prvi, koji kao drugi, a koji kao treci?
Mozda ce ti se to ciniti totalno smijesno, ali meni to nikako nije jasno 
Jer, po mojoj logici, ako pod f) raspored nije bitan, onda nije bitan ni raspored u onom pod a) jer mi je onda svejedno koji je poredak zadataka je kod prvog studenta, koji je poredak kod drugog studenta,... i onda mi taj pod a) valja.
I jos nesto... ako je opcenito bitan raspored u cijelom zadatku zasto onda u g) zadatku ne mnozimo rjesenje sa 3!^10? (kao.. prvi u svakoj grupi mozemo izabrati na 3 nacina, drugi na 2 i treci na 1 i imamo 10 grupa).
Mislim da se iz prilozenog vidi da me diskretna poprilicno puno puno zbunjuje... tj. jedino me zbunjuje to sto ne znam prepoznati kad je raspored bitan, a kad nije?
i jos nesto... jel ne bih trebala u g) dijeliti sa 10! jer studenti sami biraju grupe... pa tako da mi je svejedno kakav ce mi raspored grupa biti... jer, po mome, da je raspored grupa bitan onda bi bilo napisano na koliko nacina mogu studenti izabrati zadatke grupirane u 10 grupa od po 3 zadatka...
a moguce da sam ja u totalnoj zabludi sto se tice svega 
@ cobs & rafaelm : puno hvala 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 20:01 uto, 4. 11. 2008 Naslov: Postano: 20:01 uto, 4. 11. 2008 Naslov: |
    |
|
|
[quote="sunny"]mene uzasno zbunjuje kad je raspored bitan, a kad nije... posto na pocetku zadatka pise da su zadatci razliciti, mislila sam da je raspored svagdje bitan (dakle da mi zbog toga rjesenje pod a) ne valja). Kako da znam da mi nije bitno koji zadatak je student izabrao kao prvi, koji kao drugi, a koji kao treci?[/quote]
To ovisi o kontekstu i razumijevanju situacije. Uobicajeno je da se zadaci mogu rjesavati u kojem god redoslijedu hoces. U tom kontekstu nevazno je u kojim si ih redom birala, bitno je samo koje si izabrala, a koje nisi. Medjutim, kad bi ih morala rjesavati tocno u redoslijedu u kojem si ih birala, tada bi taj redoslijed bio bitan.
Evo dva primjera.
Na koliko nacina mozemo 30 ucenika podijeliti u tri grupe po 10 od kojih ce prva kositi travu, druga saditi cvijece, a treca piliti drva?
Rj: (30 povrh 10)*(20 povrh 10)*(10 povrh 10)
Na koliko nacina mozemo 30 ucenika podijeliti u tri grupe po 10 koje ce sve tri kositi travu?
Gornji rezultat treba podijeliti s 3! jer sve tri rade isti posao pa redoslijed nije bitan.
Matematicki receno, u prvom slucaju radi se o uredjenoj trojci medjusobno disjunktnih 10-clanih podskupova, a u drugom o particiji na 3 takva podskupa (dakle 3-clanom [b]skupu[/b] podskupova).
| sunny (napisa): | | mene uzasno zbunjuje kad je raspored bitan, a kad nije... posto na pocetku zadatka pise da su zadatci razliciti, mislila sam da je raspored svagdje bitan (dakle da mi zbog toga rjesenje pod a) ne valja). Kako da znam da mi nije bitno koji zadatak je student izabrao kao prvi, koji kao drugi, a koji kao treci? |
To ovisi o kontekstu i razumijevanju situacije. Uobicajeno je da se zadaci mogu rjesavati u kojem god redoslijedu hoces. U tom kontekstu nevazno je u kojim si ih redom birala, bitno je samo koje si izabrala, a koje nisi. Medjutim, kad bi ih morala rjesavati tocno u redoslijedu u kojem si ih birala, tada bi taj redoslijed bio bitan.
Evo dva primjera.
Na koliko nacina mozemo 30 ucenika podijeliti u tri grupe po 10 od kojih ce prva kositi travu, druga saditi cvijece, a treca piliti drva?
Rj: (30 povrh 10)*(20 povrh 10)*(10 povrh 10)
Na koliko nacina mozemo 30 ucenika podijeliti u tri grupe po 10 koje ce sve tri kositi travu?
Gornji rezultat treba podijeliti s 3! jer sve tri rade isti posao pa redoslijed nije bitan.
Matematicki receno, u prvom slucaju radi se o uredjenoj trojci medjusobno disjunktnih 10-clanih podskupova, a u drugom o particiji na 3 takva podskupa (dakle 3-clanom skupu podskupova).
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 10:13 pet, 21. 11. 2008 Naslov: Postano: 10:13 pet, 21. 11. 2008 Naslov: |
    |
|
|
Zadatak
Dan je :) pauk s osam nogu te je dano osam čarapa i toliko cipela. Na koliko načina se pauk može obući ako na svaku nogu prvo mora navući čarapu, a tek onda cipelu?
provjerite razmišljanje:
Cipele se međusobno ne razlikuju. Čarape također.
Paukove noge reprezentiram uređenom 16-torkom brojeva, gdje su prve dvije pozicije namijenjene prvoj nozi, sljedeće dvije drugoj nozi, itd.
Svaka dakle noga dolazi sa dva mjesta(uređenim parom reci), lijevo mjesto je za čarapu, a desno za cipelu.
Jedan način oblačenja pauka predstavljen je jednom 16-torkom brojeva.
Primjerice:
1 2 3 4 ... 16
Ovdje je pauk prvo obukao čarapu na prvu nogu, zatim cipelu na prvu nogu, zatim čarapu na drugu nogu, pa cipelu na drugu nogu, itd.
Svih načina obuvanja, dakle bez uvjeta zadatka da ne navlači čizmu bosonog, ima 16!.
Treba naravno izbaciti načine oblačenja koji ne zadovoljavaju uvjet zadatka.
Uzmemo li proizvoljnu nogu obučenog pauka odnosno uređeni par brojeva, način oblačenja na toj promatranoj nozi je bio dobar ako je desna komponenta uređenog para veća od lijeve komponente(tj prvo je u nekom koraku navučena čarapa, a zatim u nekom drugom koraku navučena je cipela, u suprotnom navučena je na tu nogu prvo cipela, a zatim čarapa što nije dobar način oblačenja).
Onoliko koliko ima nejednadžbi x1<x2 toliko ima i nejednadžbi x2>x1.
Stoga, ukupan broj nejednadžbi, koliki god on bio, moramo podijeliti sa dva da bismo dobili broj željenih oblačenja na toj nozi.
Noga u pauka je osam, pa dijelimo s dva osam puta,a pojedine dvojke "ljepimo" produktom.
Zato je broj oblačenja 16! / 2^8
Zadatak
Dan je  pauk s osam nogu te je dano osam čarapa i toliko cipela. Na koliko načina se pauk može obući ako na svaku nogu prvo mora navući čarapu, a tek onda cipelu? pauk s osam nogu te je dano osam čarapa i toliko cipela. Na koliko načina se pauk može obući ako na svaku nogu prvo mora navući čarapu, a tek onda cipelu?
provjerite razmišljanje:
Cipele se međusobno ne razlikuju. Čarape također.
Paukove noge reprezentiram uređenom 16-torkom brojeva, gdje su prve dvije pozicije namijenjene prvoj nozi, sljedeće dvije drugoj nozi, itd.
Svaka dakle noga dolazi sa dva mjesta(uređenim parom reci), lijevo mjesto je za čarapu, a desno za cipelu.
Jedan način oblačenja pauka predstavljen je jednom 16-torkom brojeva.
Primjerice:
1 2 3 4 ... 16
Ovdje je pauk prvo obukao čarapu na prvu nogu, zatim cipelu na prvu nogu, zatim čarapu na drugu nogu, pa cipelu na drugu nogu, itd.
Svih načina obuvanja, dakle bez uvjeta zadatka da ne navlači čizmu bosonog, ima 16!.
Treba naravno izbaciti načine oblačenja koji ne zadovoljavaju uvjet zadatka.
Uzmemo li proizvoljnu nogu obučenog pauka odnosno uređeni par brojeva, način oblačenja na toj promatranoj nozi je bio dobar ako je desna komponenta uređenog para veća od lijeve komponente(tj prvo je u nekom koraku navučena čarapa, a zatim u nekom drugom koraku navučena je cipela, u suprotnom navučena je na tu nogu prvo cipela, a zatim čarapa što nije dobar način oblačenja).
Onoliko koliko ima nejednadžbi x1<x2 toliko ima i nejednadžbi x2>x1.
Stoga, ukupan broj nejednadžbi, koliki god on bio, moramo podijeliti sa dva da bismo dobili broj željenih oblačenja na toj nozi.
Noga u pauka je osam, pa dijelimo s dva osam puta,a pojedine dvojke "ljepimo" produktom.
Zato je broj oblačenja 16! / 2^8
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
Sphiro
Forumaš(ica)
Pridružen/a: 17. 10. 2007. (16:32:45)
Postovi: (45)16
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 13:39 pet, 21. 11. 2008 Naslov: Postano: 13:39 pet, 21. 11. 2008 Naslov: |
    |
|
|
[quote="Sphiro"]Jasno je da se čarape međusobno razlikuju kao i cipele. Prvo rasporedimo čarape na 8! načina, a zatim cipele na također 8! načina, tj ukupno prema PP na 8!*8! načina.
Stoga ti je razmišljanje skroz krivo.[/quote]
Čak i da se čarape i cipele razlikuju tvoje rješenje nije dobro odnosno prebrojao si premalo načina oblačenja jer u zadatku ne piše da se prvo raspoređuju čarape, a zatim cipele.(odnosno da ide princip čarapa-cipela)
Pauku je jedino rečeno :) da ne smije obući cipelu na bosu nogu, dakle mogao je, primjerice, navući tri čarape pa dvije cipele, pa nove dvije čarape pa troje cipela(dvije na nove dvije čarape i jedna na čarapu koju je navukao u navlačenju :) troje čarapa prije).
Rezime: Ti si prebrojao načine oblačenja u kojima pauk prvo obuva sve čarape pa tek onda sve cipele(ili da je obuvao principom čarapa-cipela, ovisno kako interpretiraš broj 8!8! ).
[quote]
ovo je krivo! bitno je kad ce obuci te carape i cipele. rjesenje RonnieColemana je dobro :)[/quote]
To je Vaše rješenje sa vježbi. Ja sam samo poput forenzičara koji nailazi na leš, čitaj rješenje, rekonstruirao zločin. :mrgreen:
S ozbzirom da je asistent koji drži drugoj grupi dao rješenje 8!8! bilo bi dobro da s njime uspotavite konsenzus i javite nam odlučeno.
| Sphiro (napisa): | Jasno je da se čarape međusobno razlikuju kao i cipele. Prvo rasporedimo čarape na 8! načina, a zatim cipele na također 8! načina, tj ukupno prema PP na 8!*8! načina.
Stoga ti je razmišljanje skroz krivo. |
Čak i da se čarape i cipele razlikuju tvoje rješenje nije dobro odnosno prebrojao si premalo načina oblačenja jer u zadatku ne piše da se prvo raspoređuju čarape, a zatim cipele.(odnosno da ide princip čarapa-cipela)
Pauku je jedino rečeno  da ne smije obući cipelu na bosu nogu, dakle mogao je, primjerice, navući tri čarape pa dvije cipele, pa nove dvije čarape pa troje cipela(dvije na nove dvije čarape i jedna na čarapu koju je navukao u navlačenju da ne smije obući cipelu na bosu nogu, dakle mogao je, primjerice, navući tri čarape pa dvije cipele, pa nove dvije čarape pa troje cipela(dvije na nove dvije čarape i jedna na čarapu koju je navukao u navlačenju  troje čarapa prije). troje čarapa prije).
Rezime: Ti si prebrojao načine oblačenja u kojima pauk prvo obuva sve čarape pa tek onda sve cipele(ili da je obuvao principom čarapa-cipela, ovisno kako interpretiraš broj 8!8! ).
| Citat: |
ovo je krivo! bitno je kad ce obuci te carape i cipele. rjesenje RonnieColemana je dobro  |
To je Vaše rješenje sa vježbi. Ja sam samo poput forenzičara koji nailazi na leš, čitaj rješenje, rekonstruirao zločin. 
S ozbzirom da je asistent koji drži drugoj grupi dao rješenje 8!8! bilo bi dobro da s njime uspotavite konsenzus i javite nam odlučeno.
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 14:47 pet, 21. 11. 2008 Naslov: Postano: 14:47 pet, 21. 11. 2008 Naslov: |
    |
|
|
[quote="Atomised"]
Pa gledamo kako je na kraju obučen. Je li prvo obukao sve čarape pa onda cipele ili je prvo pola čarapa pa pola cipela pa drugu polovicu čarapa pa cipela je svejedno ako je na kraju u oba slučaja obučen jednako.[/quote]
Nije, jer u zadatku piše [b]na koliko načina se pauk može obuti[/b]...
Na koliko načina ti možeš obuti cipele bez čarapa?
Na dva načina:
-prvi je da obučeš lijevu cipelu, pa onda desnu
-drugi je da obučeš desnu cipelu, a zatim lijevu
Tako je i s paukom samo što on ima više nogu i dodatno je opterećen čarapama.
Ako pauk stavi čarapu na prvu nogu pa cipelu na prvu nogu, zatim čarapu na drugu nogu pa cipelu na tu nogu onda je to jedan način oblačenja.
Taj način predstavljam brojem 1234
Ako pauk stavi čarapu na drugu nogu pa cipelu na drugu nogu, pa čarapu na prvu nogu, pa cipelu na tu nogu onda je to jedan način oblačenja.
Način predstavljen brojem 3412
Ako pauk stavi čarapu na prvu nogu pa čarapu na drugu nogu pa cipelu na prvu nogu pa cipelu na drugu nogu, onda je to jedan način oblačenja.
1324
Ako pauk stavi čarapu na prvu nogu pa čarapu na drugu nogu pa cipelu na drugu nogu pa cipelu na prvu nogu, onda je to jedan način oblačenja.
1423
Evo ponovo pojašnjenje:
Jednostavnosti radi, neka pauk ima dvije noge:
Matematički model kojim ću reprezentirati paukove noge jest taj da ću napisati uređenu četvorku brojeva gdje su prva dva mjesta za jednu nogu, a druga dva mjesta za drugu nogu.
Lijevo mjesto je za čarapu, a desno mjesto je za cipelu.
Broj u uređenoj četvorci predstavlja korak u kojem je stavljena noga/čarapa.
Primjerice,
1234
označava da je na prvu nogu stavljena čarapa, zatim cipela na istu nogu, zatim čarapa na drugu nogu, zatim cipela na drugu nogu.
3421
označava da je na drugu nogu stavljena cipela, zatim čarapa, zatim čarapa na prvu nogu, zatim cipela na prvu nogu.
Primjeti da ako se cipele i čarape razlikuju onda rješenje postaje još teže:
č1 čarapa prve vrste
c1 cipela prve vrste
č2 i c2 analogno
č1 c1 č2 c2
Postupak oblačenja:
1234
2314
1324
1423
2413
3412
č1 c2 č2 c1
iste permutacije kao gore
č2 c1 č1 c2
-||-
č2 c2 č1 c1
-||-
| Atomised (napisa): |
Pa gledamo kako je na kraju obučen. Je li prvo obukao sve čarape pa onda cipele ili je prvo pola čarapa pa pola cipela pa drugu polovicu čarapa pa cipela je svejedno ako je na kraju u oba slučaja obučen jednako. |
Nije, jer u zadatku piše na koliko načina se pauk može obuti...
Na koliko načina ti možeš obuti cipele bez čarapa?
Na dva načina:
-prvi je da obučeš lijevu cipelu, pa onda desnu
-drugi je da obučeš desnu cipelu, a zatim lijevu
Tako je i s paukom samo što on ima više nogu i dodatno je opterećen čarapama.
Ako pauk stavi čarapu na prvu nogu pa cipelu na prvu nogu, zatim čarapu na drugu nogu pa cipelu na tu nogu onda je to jedan način oblačenja.
Taj način predstavljam brojem 1234
Ako pauk stavi čarapu na drugu nogu pa cipelu na drugu nogu, pa čarapu na prvu nogu, pa cipelu na tu nogu onda je to jedan način oblačenja.
Način predstavljen brojem 3412
Ako pauk stavi čarapu na prvu nogu pa čarapu na drugu nogu pa cipelu na prvu nogu pa cipelu na drugu nogu, onda je to jedan način oblačenja.
1324
Ako pauk stavi čarapu na prvu nogu pa čarapu na drugu nogu pa cipelu na drugu nogu pa cipelu na prvu nogu, onda je to jedan način oblačenja.
1423
Evo ponovo pojašnjenje:
Jednostavnosti radi, neka pauk ima dvije noge:
Matematički model kojim ću reprezentirati paukove noge jest taj da ću napisati uređenu četvorku brojeva gdje su prva dva mjesta za jednu nogu, a druga dva mjesta za drugu nogu.
Lijevo mjesto je za čarapu, a desno mjesto je za cipelu.
Broj u uređenoj četvorci predstavlja korak u kojem je stavljena noga/čarapa.
Primjerice,
1234
označava da je na prvu nogu stavljena čarapa, zatim cipela na istu nogu, zatim čarapa na drugu nogu, zatim cipela na drugu nogu.
3421
označava da je na drugu nogu stavljena cipela, zatim čarapa, zatim čarapa na prvu nogu, zatim cipela na prvu nogu.
Primjeti da ako se cipele i čarape razlikuju onda rješenje postaje još teže:
č1 čarapa prve vrste
c1 cipela prve vrste
č2 i c2 analogno
č1 c1 č2 c2
Postupak oblačenja:
1234
2314
1324
1423
2413
3412
č1 c2 č2 c1
iste permutacije kao gore
č2 c1 č1 c2
-||-
č2 c2 č1 c1
-||-
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
RonnieColeman
Forumaš(ica)

Pridružen/a: 26. 04. 2006. (10:35:00)
Postovi: (20B)16
Spol: 
Lokacija: |R^3
|
 Postano: 16:53 pet, 21. 11. 2008 Naslov: Postano: 16:53 pet, 21. 11. 2008 Naslov: |
    |
|
|
[quote="Cobs"][quote="RonnieColeman"]Zato je broj oblačenja 16! / 2^8[/quote]
kad smo rješavali mislim da smo govorili kako [b]prvo[/b] treba obući pauku [b]sve[/b] čarape, a zatim cipele[/quote]
To ne piše u tekstu zadatka pa ćeš se složiti samnom :) da je u tom slučaju zadatak neprecizno zadan.
Ipak, to je način na koji je vaš asistent rješavao zadatak.
[quote="Cobs"]
u slučaju da nam je bitno da mu obučemo čarapu prije cipele mislim da je tvoje rješenje točno[/quote]
U svakom slučaju, navlačili prvo sve čarape ili ne, bitno je da se čarapa navuče prije čizme. :)
| Cobs (napisa): | | RonnieColeman (napisa): | | Zato je broj oblačenja 16! / 2^8 |
kad smo rješavali mislim da smo govorili kako prvo treba obući pauku sve čarape, a zatim cipele |
To ne piše u tekstu zadatka pa ćeš se složiti samnom  da je u tom slučaju zadatak neprecizno zadan. da je u tom slučaju zadatak neprecizno zadan.
Ipak, to je način na koji je vaš asistent rješavao zadatak.
| Cobs (napisa): |
u slučaju da nam je bitno da mu obučemo čarapu prije cipele mislim da je tvoje rješenje točno |
U svakom slučaju, navlačili prvo sve čarape ili ne, bitno je da se čarapa navuče prije čizme. 
_________________
...He never had looked less like captain of any-thing, even his own soul.
|
|
| [Vrh] |
|
|















