| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Izgubljen u prijevodu
Forumaš(ica)

Pridružen/a: 19. 11. 2007. (12:57:54)
Postovi: (A)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 18:47 čet, 13. 11. 2008 Naslov: Postano: 18:47 čet, 13. 11. 2008 Naslov: |
    |
|
|
Ako sam dobro shvatio treba ispitati konvergenciju reda :
[latex]\displaystyle \sum_{n=5}^{\infty} ln(\frac{1}{\cos(\frac{2 \pi}{n})})[/latex]
D'Alembertov kriterij + sve sto je Luuka rekao, bi funkcioniralo kada bi bilo [latex]\frac{ln x}{ln y}=ln{\frac{x}{y}}[/latex], e buduci da nije tako moramo se drugacije snaci...
Prvo uocimo da je [latex]\displaystyle ln(\frac{1}{\cos(\frac{2 \pi}{n})})=-ln(\cos{\frac{2\pi}{n}})[/latex].
Nadalje;
[latex]\cos{x}=1-\mathcal{O}_0(x^3)(*) \newline
\ln (1-x)=-\mathcal{O}_0(x)[/latex].
I sada prepustam Luuki da zavrsi zadatak :D... ( nije tako tesko dobiti cete da je [latex]\displaystyle \sum_{n=5}^{\infty} ln(\frac{1}{\cos(\frac{2 \pi}{n})})=\sum_n \mathcal{O}_0(n^{-p})[/latex] gdje ce [latex]p[/latex] biti veci od 1 :wink: )
[size=9][color=#999999]Added after 12 minutes:[/color][/size]
[quote="Luuka"]Usporedni kriterij.
-1 <= cosn <= 1.
pa red divergira ;)[/quote]
E moj Luuka, danas nesta nisi u formi... Uzmimo neki [latex]c\in \mathbb{R}[/latex] dovoljno velik, tada je [latex]-1\leq\sin{\frac{c}{n}}\leq 1,\forall n[/latex] ( ovo radim samo da ima negativnih clanova, pa da bude slicnost sa orginalnim problemom ), a red [latex]\displaystyle \sum_n \frac{\sin{\frac{c}{n}}}{n}[/latex] konvergira ( jer je opci clan oblika [latex]\mathcal{O}_0(n^{-2})[/latex] )
Edit: ako ste procitali moj zadnji posta onda kuzite da sam kod (*) pogrijesio, naime treba biti;
[latex]\cos{x}=1-\mathcal{O}_0(x^2)[/latex]
Ako sam dobro shvatio treba ispitati konvergenciju reda :
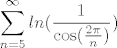
D'Alembertov kriterij + sve sto je Luuka rekao, bi funkcioniralo kada bi bilo 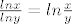 , e buduci da nije tako moramo se drugacije snaci... , e buduci da nije tako moramo se drugacije snaci...
Prvo uocimo da je 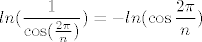 . .
Nadalje;
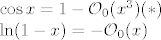 . .
I sada prepustam Luuki da zavrsi zadatak  ... ( nije tako tesko dobiti cete da je ... ( nije tako tesko dobiti cete da je 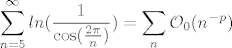 gdje ce gdje ce  biti veci od 1 biti veci od 1  ) )
Added after 12 minutes:
| Luuka (napisa): | Usporedni kriterij.
-1 ⇐ cosn ⇐ 1.
pa red divergira  |
E moj Luuka, danas nesta nisi u formi... Uzmimo neki 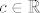 dovoljno velik, tada je dovoljno velik, tada je 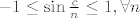 ( ovo radim samo da ima negativnih clanova, pa da bude slicnost sa orginalnim problemom ), a red ( ovo radim samo da ima negativnih clanova, pa da bude slicnost sa orginalnim problemom ), a red 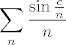 konvergira ( jer je opci clan oblika konvergira ( jer je opci clan oblika 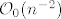 ) )
Edit: ako ste procitali moj zadnji posta onda kuzite da sam kod (*) pogrijesio, naime treba biti;
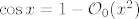
Zadnja promjena: Mr.Doe; 19:32 čet, 13. 11. 2008; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 19:29 čet, 13. 11. 2008 Naslov: Postano: 19:29 čet, 13. 11. 2008 Naslov: |
    |
|
|
Ma nije bed Luuka, samo ti pisi, bolje ti je da vjezbas, a uostalom i najbolji ponekad pogrijese...
Cudno da niste culi za Landau-ove simbole, mi smo to jos radili na Analizi, ako ne tamo onda ziher na Numerickoj. Uostalom poanta ti je u ovome, ja imam neku ful tesku funkciju, npr. kao ova u prvom zadatku, a sada ja bi je na nekoj okolini tocke htio kontrolirati sa nekom drugom funkcijom, ali naravno zahtjevam da je ta funkcija puno jednostavnija ( kao sta vidis ja stalno lupam neke polinome ). Sada formalna definicija ti je;
[latex]f(x)=\mathcal{O}_{x_0}(g(x))[/latex], ako na nekoj okolini tocke [latex]x_0[/latex] vrijedi [latex]|f(x)|\leq C|g(x)|[/latex] gdje je C neka pozitivna konstanta .
Nadam se da vidis u cemu je stos; mene uopce ne zanima kolika je ta konstanta! I upravo kod redova i limesa ove stvari dolaze do izrazaja.
Na primjer, promotrimo limes [latex]\lim_{x\rightarrow 0}\frac{\sin x}{x}[/latex] ( ovo je ful jednostavno ).
Sta je znam;
[latex]\sin x=x-\mathcal{O}_0(x^3})[/latex], sada to podijelim sa x i dobijem [latex]\lim_{x\rightarrow 0}1-\mathcal{O}_0(x^2})[/latex], i ja sada moram ustanoviti nesta ful jednostavno, a to je da [latex]C|x^2|[/latex] tezi ka nuli, kada x ide u nulu bez obzira na konstantu C.
Naravno ti se mozes zapitati od kuda ja znam da je [latex]\sin x=x-\mathcal{O}_0(x^3})[/latex], no to nije nesta drugo nego Taylorov teorem ! ( samo ti Taylorov teorem kaze kolika je ta konstanta ).
Kao sto vidis ovo moze jako pojednostaviti neke probleme, samo treba biti spretan sa tim manipulacijama i ne moze fulati.
Imas na wikipediji o tome, korisno je pogledati, ali ful me cudi da vam to nisu pokazali na analizi ( sjecam se da je Ilja to pokazivao... )
Edit: samo da jos nadodam, ove stvari se mogu takoder koristit kod redova, a klasicna je primjena sljedeca, imas neku funkciju [latex]f[/latex], na skupu prirodnih brojeva ( no ti je tretiras kao da je definirana na R ), nekim manipulacijama, npr razvijanjem u red, dobijes
[latex]\sum_nf(n)=\sum_n \mathcal{O}_0(n^{-p})[/latex] i ako je p veci od jedan gotov si, red konvergira, jer [latex]\sum_nn^{-p}[/latex] konvergira za p veci o jedan, i nema nikakve veze sa kakvom si konstantom pomozio taj red.
Ma nije bed Luuka, samo ti pisi, bolje ti je da vjezbas, a uostalom i najbolji ponekad pogrijese...
Cudno da niste culi za Landau-ove simbole, mi smo to jos radili na Analizi, ako ne tamo onda ziher na Numerickoj. Uostalom poanta ti je u ovome, ja imam neku ful tesku funkciju, npr. kao ova u prvom zadatku, a sada ja bi je na nekoj okolini tocke htio kontrolirati sa nekom drugom funkcijom, ali naravno zahtjevam da je ta funkcija puno jednostavnija ( kao sta vidis ja stalno lupam neke polinome ). Sada formalna definicija ti je;
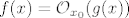 , ako na nekoj okolini tocke , ako na nekoj okolini tocke  vrijedi vrijedi 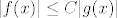 gdje je C neka pozitivna konstanta . gdje je C neka pozitivna konstanta .
Nadam se da vidis u cemu je stos; mene uopce ne zanima kolika je ta konstanta! I upravo kod redova i limesa ove stvari dolaze do izrazaja.
Na primjer, promotrimo limes 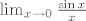 ( ovo je ful jednostavno ). ( ovo je ful jednostavno ).
Sta je znam;
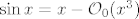 , sada to podijelim sa x i dobijem , sada to podijelim sa x i dobijem 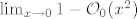 , i ja sada moram ustanoviti nesta ful jednostavno, a to je da , i ja sada moram ustanoviti nesta ful jednostavno, a to je da 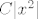 tezi ka nuli, kada x ide u nulu bez obzira na konstantu C. tezi ka nuli, kada x ide u nulu bez obzira na konstantu C.
Naravno ti se mozes zapitati od kuda ja znam da je 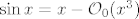 , no to nije nesta drugo nego Taylorov teorem ! ( samo ti Taylorov teorem kaze kolika je ta konstanta ). , no to nije nesta drugo nego Taylorov teorem ! ( samo ti Taylorov teorem kaze kolika je ta konstanta ).
Kao sto vidis ovo moze jako pojednostaviti neke probleme, samo treba biti spretan sa tim manipulacijama i ne moze fulati.
Imas na wikipediji o tome, korisno je pogledati, ali ful me cudi da vam to nisu pokazali na analizi ( sjecam se da je Ilja to pokazivao... )
Edit: samo da jos nadodam, ove stvari se mogu takoder koristit kod redova, a klasicna je primjena sljedeca, imas neku funkciju  , na skupu prirodnih brojeva ( no ti je tretiras kao da je definirana na R ), nekim manipulacijama, npr razvijanjem u red, dobijes , na skupu prirodnih brojeva ( no ti je tretiras kao da je definirana na R ), nekim manipulacijama, npr razvijanjem u red, dobijes
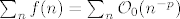 i ako je p veci od jedan gotov si, red konvergira, jer i ako je p veci od jedan gotov si, red konvergira, jer 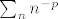 konvergira za p veci o jedan, i nema nikakve veze sa kakvom si konstantom pomozio taj red. konvergira za p veci o jedan, i nema nikakve veze sa kakvom si konstantom pomozio taj red.
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 16:44 pet, 14. 11. 2008 Naslov: Postano: 16:44 pet, 14. 11. 2008 Naslov: |
    |
|
|
Ispravio sam jos pola sata prije nego sto si postavila pitanje :D .
Inace, ovo sto si napisala je ( skoro ) tocno no krajnje nekorisno. Dakle, sta Taylorov teorem kaze;
ako imam funkciju [latex]f[/latex] klase [latex]C^n[/latex], onda na okolini tocke [latex]x[/latex]
[latex]f(x+h)=f(x)+f'(x)h+\dots+\frac{f^{(n)}(\xi)}{n!}h^n[/latex], necu ulaziti u to gdje je tocno [latex]\xi[/latex] nije bitno u ovom trenutku.
Naime, vrijedi sljedece; [latex]x^n=\mathcal{O}_0(x^m)[/latex] za [latex]m<n[/latex], to se lako vidi, npr. [latex]x^2[/latex] brze tezi k nuli nego [latex]x[/latex] na nekoj okolini od nule. Sada, cosinus je analiticka funkcija, ma nemamo nikakvih problema; pa slijedi
[latex]\cos{x}=1-\frac{x^2}{2!}+\frac{\cos^{(4)}{(\xi)}}{4!}x^4[/latex], odnosno
[latex]\cos{x}=1-\frac{x^2}{2!}+\mathcal{O}_0(x^4)[/latex], naravno ti sada mozes napisati [latex]\cos{x}=1-\frac{x^2}{2!}+\mathcal{O}_0(x^2)[/latex], no tebi nije poanta kontrolirati taj ostatak sa proizvoljnom funkcijom, nego sa najboljom mogucom. Na primjer;
Zamisli da te upitam da li red [latex]\sum_n n^{-2}[/latex] konvergira, u analogiji sa tvojim komentarom, ti bi mi rekla da [latex]n^{-2}\leq n^{-1}[/latex], no nazalost ta informacija mi nista ne govori ( jer harmonijski red divergira ), korisnija bi informacija bila [latex]n^{-2}\leq n^{-p},2\geq p>1[/latex], i da zatim pokazes da red [latex]\sum_n n^{-p},~p>1[/latex] konvergira.
Ispravio sam jos pola sata prije nego sto si postavila pitanje  . .
Inace, ovo sto si napisala je ( skoro ) tocno no krajnje nekorisno. Dakle, sta Taylorov teorem kaze;
ako imam funkciju  klase klase  , onda na okolini tocke , onda na okolini tocke 
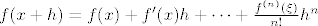 , necu ulaziti u to gdje je tocno , necu ulaziti u to gdje je tocno 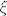 nije bitno u ovom trenutku. nije bitno u ovom trenutku.
Naime, vrijedi sljedece; 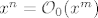 za za 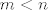 , to se lako vidi, npr. , to se lako vidi, npr. 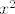 brze tezi k nuli nego brze tezi k nuli nego  na nekoj okolini od nule. Sada, cosinus je analiticka funkcija, ma nemamo nikakvih problema; pa slijedi na nekoj okolini od nule. Sada, cosinus je analiticka funkcija, ma nemamo nikakvih problema; pa slijedi
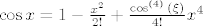 , odnosno , odnosno
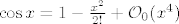 , naravno ti sada mozes napisati , naravno ti sada mozes napisati 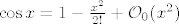 , no tebi nije poanta kontrolirati taj ostatak sa proizvoljnom funkcijom, nego sa najboljom mogucom. Na primjer; , no tebi nije poanta kontrolirati taj ostatak sa proizvoljnom funkcijom, nego sa najboljom mogucom. Na primjer;
Zamisli da te upitam da li red 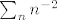 konvergira, u analogiji sa tvojim komentarom, ti bi mi rekla da konvergira, u analogiji sa tvojim komentarom, ti bi mi rekla da 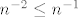 , no nazalost ta informacija mi nista ne govori ( jer harmonijski red divergira ), korisnija bi informacija bila , no nazalost ta informacija mi nista ne govori ( jer harmonijski red divergira ), korisnija bi informacija bila 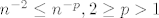 , i da zatim pokazes da red , i da zatim pokazes da red 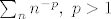 konvergira. konvergira.
|
|
| [Vrh] |
|
vriskica
Forumaš(ica)

Pridružen/a: 15. 08. 2008. (16:44:24)
Postovi: (73)16
|
|
| [Vrh] |
|
|









