| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Debla
Forumaš(ica)
Pridružen/a: 06. 12. 2005. (16:54:24)
Postovi: (94)16
Spol: 
|
|
| [Vrh] |
|
desire
Forumaš(ica)
Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol:
|
 Postano: 20:30 uto, 18. 11. 2008 Naslov: |
    |
|
|
[quote="Luuka"]e beba, beba, imaš slično u vježbama... ;)
Uglavnom, fja distribucije od y je:
Fy(Y) = P (Y<=y) = P(1/X<=y)
sad posebno slučajevi pozitivno i negativno pa sve svest na X za kojeg znamo i distribuciju i gustoću... toliko ukratko, pa pitaj ak ne uspiješ ;)[/quote]
ja ne uspjevam i gotovo... :( porjesavala sam hrpu zadataka i ovdje blokirala... help.... :pray:
[size=7]znam da ima slicno na vjezbma, ali ja ne znam kaj bi s ovim (mogu se kladit da je neka glupost, al dobro)... [/size] :D
| Luuka (napisa): | e beba, beba, imaš slično u vježbama... 
Uglavnom, fja distribucije od y je:
Fy(Y) = P (Y⇐y) = P(1/X⇐y)
sad posebno slučajevi pozitivno i negativno pa sve svest na X za kojeg znamo i distribuciju i gustoću... toliko ukratko, pa pitaj ak ne uspiješ |
ja ne uspjevam i gotovo...  porjesavala sam hrpu zadataka i ovdje blokirala... help.... 
znam da ima slicno na vjezbma, ali ja ne znam kaj bi s ovim (mogu se kladit da je neka glupost, al dobro)... 
_________________  |
|
| [Vrh] |
|
tihana
Forumaš(ica)
Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
Debla
Forumaš(ica)
Pridružen/a: 06. 12. 2005. (16:54:24)
Postovi: (94)16
Spol:
|
|
| [Vrh] |
|
Manny Callavera
Forumaš(ica)
Pridružen/a: 17. 02. 2004. (12:40:20)
Postovi: (2D)16
Spol: 
Lokacija: Zgb
|
| Postano: 1:18 sri, 19. 11. 2008 Naslov: Mala pomoc |
|
|
|
Poz, Debla
(Zad 2.22) glasi:
X ~N(mi,sigma^2). Odredite funkciju distribucije Y = alfa*X+beta,tj.
P(Y<x) za proizv. x neki.
rj.
P(Y<x)=P(alfa*X+beta < x)={Dogadjaj alfaX+beta < x je jednak dogadjaju X <(x-beta)/alfa, pa zato imamo..}=P(X < (x-beta)/alfa )={ ako sada na obje strane nejednakosti oduzmem 'mi' i obje strane podijelim sa 'sigma' i sve sredim da nemam dvojnih razlomaka, nejednakost se opet nije promijenila,novi dogadjaj je opet analogan pocetnom} =
P([X -mi]/[sigma] < [x-('alfa'*'mi'+beta)]/['sigma'*'alfa'])={samo sto je sada sl. varijabla
[X -mi]/[sigma]~N(0,1)a njenu fju distribucije znamo, pa sada trebaš izračunati F_x([x-('alfa'*'mi'+beta)]/['sigma'*'alfa'])}.
Imaš sada:
fju distribucije od jedinične normalne samo što u gornjoj granici piše
[x-('alfa'*'mi'+beta)]/['sigma'*'alfa'], a ti zelis da u gornjoj granici pise samo x.
Recimo da integriras svoj integral po varijabli t, uzmi supstituciju
t=(1/sigma*alfa)U-(alfa*mi+beta), pa kada t->-beskonacno onda u-> -beskonacno, a kada t->[x-('alfa'*'mi'+beta)]/['sigma'*'alfa'] tvoj u->x.
Imas jos dt=(1/sigma*alfa)du.
Nakon toga dobijes integral koji odgovara funkciji distribucije sl. varijable Y~N(alfa*mi+beta, sigma^2 *alfa^2).
Mozda pomogne ;)
Poz, Debla
(Zad 2.22) glasi:
X ~N(mi,sigma^2). Odredite funkciju distribucije Y = alfa*X+beta,tj.
P(Y<x) za proizv. x neki.
rj.
P(Y<x)=P(alfa*X+beta < x)={Dogadjaj alfaX+beta < x je jednak dogadjaju X <(x-beta)/alfa, pa zato imamo..}=P(X < (x-beta)/alfa )={ ako sada na obje strane nejednakosti oduzmem 'mi' i obje strane podijelim sa 'sigma' i sve sredim da nemam dvojnih razlomaka, nejednakost se opet nije promijenila,novi dogadjaj je opet analogan pocetnom} =
P([X -mi]/[sigma] < [x-('alfa'*'mi'+beta)]/['sigma'*'alfa'])={samo sto je sada sl. varijabla
[X -mi]/[sigma]~N(0,1)a njenu fju distribucije znamo, pa sada trebaš izračunati F_x([x-('alfa'*'mi'+beta)]/['sigma'*'alfa'])}.
Imaš sada:
fju distribucije od jedinične normalne samo što u gornjoj granici piše
[x-('alfa'*'mi'+beta)]/['sigma'*'alfa'], a ti zelis da u gornjoj granici pise samo x.
Recimo da integriras svoj integral po varijabli t, uzmi supstituciju
t=(1/sigma*alfa)U-(alfa*mi+beta), pa kada t→-beskonacno onda u→ -beskonacno, a kada t→[x-('alfa'*'mi'+beta)]/['sigma'*'alfa'] tvoj u→x.
Imas jos dt=(1/sigma*alfa)du.
Nakon toga dobijes integral koji odgovara funkciji distribucije sl. varijable Y~N(alfa*mi+beta, sigma^2 *alfa^2).
Mozda pomogne
|
|
| [Vrh] |
|
desire
Forumaš(ica)
Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol:
|
|
| [Vrh] |
|
Debla
Forumaš(ica)
Pridružen/a: 06. 12. 2005. (16:54:24)
Postovi: (94)16
Spol:
|
|
| [Vrh] |
|
desire
Forumaš(ica)
Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol:
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
| Postano: 10:58 sri, 19. 11. 2008 Naslov: |
|
|
|
[quote="desire"]Jel mi moze netko objasniti zadatak 2.11. Odakle oni (4-2x)(3-2x)??
I jel rijesio netko 6. zadatak iz kolokvija?[/quote]
2.11: nacrtaš si taj pravokutnik i one pravce za koje je udaljenost =x0 (sad samo oznaka, to je onaj naš x u zad). To su pravci x=x0, x=4-x0, y=x0 i y=3-x0. Nama treba udaljenost bit >=x0, a ta udaljenost se postiže da one točke unutar tog malog pravokutnika... i sad je naša vjerojatnost površina_malog/površina_velikog.
U 6.zad u kolokviju odrediš C t.d je dvostr integral fje gustoće =1, paziš na granice, di ti je fja gustoće različita od 0...
a pod b) (prva grupa) trebaš nać fju gustoće od Y (marginalnu gustoću) i onda E[Y^2]- (E[Y])^2.
| desire (napisa): | Jel mi moze netko objasniti zadatak 2.11. Odakle oni (4-2x)(3-2x)??
I jel rijesio netko 6. zadatak iz kolokvija? |
2.11: nacrtaš si taj pravokutnik i one pravce za koje je udaljenost =x0 (sad samo oznaka, to je onaj naš x u zad). To su pravci x=x0, x=4-x0, y=x0 i y=3-x0. Nama treba udaljenost bit >=x0, a ta udaljenost se postiže da one točke unutar tog malog pravokutnika... i sad je naša vjerojatnost površina_malog/površina_velikog.
U 6.zad u kolokviju odrediš C t.d je dvostr integral fje gustoće =1, paziš na granice, di ti je fja gustoće različita od 0...
a pod b) (prva grupa) trebaš nać fju gustoće od Y (marginalnu gustoću) i onda E[Y^2]- (E[Y])^2.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy |
|
| [Vrh] |
|
desire
Forumaš(ica)
Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol:
|
| Postano: 11:30 sri, 19. 11. 2008 Naslov: |
|
|
|
[quote="Luuka"][quote="desire"]Jel mi moze netko objasniti zadatak 2.11. Odakle oni (4-2x)(3-2x)??
I jel rijesio netko 6. zadatak iz kolokvija?[/quote]
2.11: nacrtaš si taj pravokutnik i one pravce za koje je udaljenost =x0 (sad samo oznaka, to je onaj naš x u zad). To su pravci x=x0, x=4-x0, y=x0 i y=3-x0. Nama treba udaljenost bit >=x0, a ta udaljenost se postiže da one točke unutar tog malog pravokutnika... i sad je naša vjerojatnost površina_malog/površina_velikog.
U 6.zad u kolokviju odrediš C t.d je dvostr integral fje gustoće =1, paziš na granice, di ti je fja gustoće različita od 0...
a pod b) (prva grupa) trebaš nać fju gustoće od Y (marginalnu gustoću) i onda E[Y^2]- (E[Y])^2.[/quote]
Hvala Luuka. A sto se tice 6. iz kolokvija, znam ja kak se odredjuje C, al se ne mogu isprtljat iz integrala... :D
| Luuka (napisa): | | desire (napisa): | Jel mi moze netko objasniti zadatak 2.11. Odakle oni (4-2x)(3-2x)??
I jel rijesio netko 6. zadatak iz kolokvija? |
2.11: nacrtaš si taj pravokutnik i one pravce za koje je udaljenost =x0 (sad samo oznaka, to je onaj naš x u zad). To su pravci x=x0, x=4-x0, y=x0 i y=3-x0. Nama treba udaljenost bit >=x0, a ta udaljenost se postiže da one točke unutar tog malog pravokutnika... i sad je naša vjerojatnost površina_malog/površina_velikog.
U 6.zad u kolokviju odrediš C t.d je dvostr integral fje gustoće =1, paziš na granice, di ti je fja gustoće različita od 0...
a pod b) (prva grupa) trebaš nać fju gustoće od Y (marginalnu gustoću) i onda E[Y^2]- (E[Y])^2. |
Hvala Luuka. A sto se tice 6. iz kolokvija, znam ja kak se odredjuje C, al se ne mogu isprtljat iz integrala...
_________________ |
|
| [Vrh] |
|
stuey
Forumaš(ica)
Pridružen/a: 03. 11. 2006. (15:52:11)
Postovi: (A2)16
Spol:
Lokacija: Rijeka, Zg
|
| Postano: 11:31 sri, 19. 11. 2008 Naslov: |
|
|
|
[quote="Debla"]hvala ,hvala :D
e sad bi mi trebali 2.20. 2.22.
ako bi mozda bilo dobrih ljudi koji bi mogli stavit rješenje za te zadatke pliz..[/quote]
jel 2.20 onaj s beta-distribucijom? moram pitat jer izgleda da svatko ima neki drugi materijal :)
ako se radi o tome, onda kod EX izvučeš 1/B(p,q) van integrala, a taj integral će ti biti B(p+1,q) pa to izraziš pomoću formule iz prethodnog zadatka (pomoću lambda fje), i pokrati se dosta toga :)
a E[X^n] se indukcijom može pokazati da je [latex]\frac{(p+n-1)(p+n-2)...(p+1)p}{(p+q+n-1)(p+q+n-2)...(p+q+1)(p+q)}[/latex], što se da ljepše zapisat pomoću faktorijela, ali tko će to sad :D
| Debla (napisa): | hvala ,hvala
e sad bi mi trebali 2.20. 2.22.
ako bi mozda bilo dobrih ljudi koji bi mogli stavit rješenje za te zadatke pliz.. |
jel 2.20 onaj s beta-distribucijom? moram pitat jer izgleda da svatko ima neki drugi materijal 
ako se radi o tome, onda kod EX izvučeš 1/B(p,q) van integrala, a taj integral će ti biti B(p+1,q) pa to izraziš pomoću formule iz prethodnog zadatka (pomoću lambda fje), i pokrati se dosta toga
a E[X^n] se indukcijom može pokazati da je 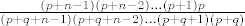 , što se da ljepše zapisat pomoću faktorijela, ali tko će to sad
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
shimija
Forumaš(ica)
Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
|
| [Vrh] |
|
matmih
Forumaš(ica)
Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol:
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
mladac
Forumaš(ica)
Pridružen/a: 24. 10. 2005. (22:46:14)
Postovi: (4D5)16
Spol:
Lokacija: zg
|
|
| [Vrh] |
|
tihana
Forumaš(ica)
Pridružen/a: 19. 06. 2006. (13:26:54)
Postovi: (30D)16
Spol:
Lokacija: Zagreb
|
|
| [Vrh] |
|
teja
Forumaš(ica)
Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol:
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
|
