| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
 Postano: 2:16 sub, 8. 11. 2008 Naslov: 3. zadaca Postano: 2:16 sub, 8. 11. 2008 Naslov: 3. zadaca |
    |
|
|
evo, za pocetak bih molio nekakav hint, uputu i sl za 4. zadatak:
dokazite da je broj particija skupa [latex]\{1,...,n\}[/latex] koje imaju svojstvo da se susjedni brojevi nikada ne javljaju u istom clanu particije dan s [latex]B_{n-1}[/latex].
e sad, [latex]B_{n-1}[/latex] je broj svih mogucih particija [latex](n-1)[/latex]-clanog skupa, dok mi krecemo od [latex]n[/latex]-clanog skupa...
ako je npr. [latex]n=6[/latex], vidim da uzimamo u obzir particije poput npr. [latex]\{\{1,4,6\},\{2\},\{3,5\}\}[/latex] (niti u jednom bloku particije nema susjednih brojeva), i pitanje je kako doci do toga da je broj svih takvih particija zapravo [latex]B_5[/latex]? :shock:
duboko zahvalan!
evo, za pocetak bih molio nekakav hint, uputu i sl za 4. zadatak:
dokazite da je broj particija skupa 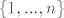 koje imaju svojstvo da se susjedni brojevi nikada ne javljaju u istom clanu particije dan s koje imaju svojstvo da se susjedni brojevi nikada ne javljaju u istom clanu particije dan s 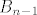 . .
e sad, 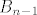 je broj svih mogucih particija je broj svih mogucih particija  -clanog skupa, dok mi krecemo od -clanog skupa, dok mi krecemo od  -clanog skupa... -clanog skupa...
ako je npr. 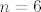 , vidim da uzimamo u obzir particije poput npr. , vidim da uzimamo u obzir particije poput npr. 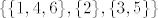 (niti u jednom bloku particije nema susjednih brojeva), i pitanje je kako doci do toga da je broj svih takvih particija zapravo (niti u jednom bloku particije nema susjednih brojeva), i pitanje je kako doci do toga da je broj svih takvih particija zapravo 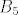 ? ? 
duboko zahvalan!
_________________  |
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
 Postano: 16:42 ned, 9. 11. 2008 Naslov: Postano: 16:42 ned, 9. 11. 2008 Naslov: |
    |
|
|
[quote="goc"]znaci radis ovakvo preslikavanje. ako u nekom clanu particije n-1 brojeva imas uzastopne, uzmes cijeli taj niz brojeva i iz njega izbacujes parne zdesna. znaci ako imas 1234 izbacis 1 i 3, ak imas 12345 izbacis 2 i 4 i tako dalje.. sve te brojeve koje si izbacio potrpas u jedan novi skup(clan) i tamo jos dodas broj n. tada je to particija n brojeva takva da nema susjednih u istom clanu particije.. sad jos treba pokazat da je takvo preslikavanje bijektivno, to dalje nastavi :)[/quote]
E, upravo me muci kako pokazati da je opisano preslikavanje stvarno bijekcija, koja "pokupi" bas sve particije sa trazenim svojstvom. Bio bih jako zahvalan za neki hint, smjernicu...
Pokusao sam raspisati:
Znamo da je [latex]B_{n-1}[/latex] broj svih particija [latex](n-1)[/latex]-clanog skupa. Ako je taj broj jednak broju svih particija [latex]n[/latex]-clanog skupa koje imaju svojstvo da se ni u jednom bloku particije ne nalaze dva susjedna broja, onda mozemo uspostaviti bijekciju izmedju
skupa koji se sastoji od svih particija [latex](n-1)[/latex]-clanog skupa i
skupa koji se sastoji od svih particija [latex]n[/latex]-clanog skupa u cijim blokovima nema susjednih brojeva,
na sljedeci nacin:
ako imamo neku particiju [latex]\pi[/latex] skupa [latex]\{1,...,n-1\}[/latex], oznacimo sa [latex]i,i+1,...,j[/latex] gdje je [latex]j>i[/latex], maksimalno dugacak niz dva ili vise uzastopna broja u nekom bloku particije [latex]\pi[/latex]. Iz ovako oznacenog niza izbacimo clanove [latex]j-1,j-3,j-5,...[/latex] i ubacimo ih u skup [latex]\{n\}[/latex]. Ovaj postupak ponovimo za sve nizove uzastopnih brojeva u particiji.
Ocito je da uz [latex]n[/latex] ne moze doci [latex]n-1[/latex], jer uvijek biramo manji od dva uzastopna broja, odnosno ako se u nekome koraku u skupu koji sadrzi [latex]n[/latex] i u koji ubacujemo brojeve nalazi neki [latex]i[/latex], uz njega ne mogu doci ni [latex]i+1[/latex] (koji, kao veci broj, ostaje u svom skupu), ni [latex]i-1[/latex] (jer njega ne ubacujemo u skup sa [latex]n[/latex] jer se uz njega ne nalazi [latex]i[/latex]).
Pogledajmo prvo, na primjeru skupa {1,2,3,4}, koje nam sve particije odgovaraju (particije bez uzastopnih brojeva u blokovima su zaplavljene):
[kraca oznaka: {{1,2,3},{4}} = 123-4]
[color=blue]
[b]1-2-3-4[/b][/color]
12-3-4
[color=blue][b]13-2-4[/b][/color]
[color=blue][b]14-2-3[/b][/color]
23-1-4
[color=blue][b]24-1-3[/b][/color]
34-1-2
123-4
124-3
134-2
234-1
12-34
[color=blue][b]13-24[/b][/color]
14-23
1234
Mozemo li sve te zaplavljene particije dobiti gore opisanim postupkom?
Sve particije skupa {1,2,3} su:
{{1,2,3}} => ovdje imamo niz od tri uzastopna broja, izbacujemo (j-1)=2 i dodajemo ga u {4} kako bismo dobili particiju {{1,3},{2,4}} tj. [color=blue][b]13-24[/b][/color]
{{1,2},{3}} => iz prvog bloka izbacujemo 1 i stavljamo ga u {4} kako bismo dobili particiju {{2},{3},{1,4}} tj. [color=blue][b]14-2-3[/b][/color]
{{1,3},{2}} => nema blokova sa uzastopnim brojevima pa {4} "dodajemo prazan skup" kako bismo dobili particiju {{1,3},{2},{4}} tj. [color=blue][b]13-2-4[/b][/color]
{{2,3},{1}} => iz prvog bloka izbacujemo 2 i stavljamo ga u {4} kako bismo dobili particiju {{3},{1},{2,4}} tj. [color=blue][b]24-1-3[/b][/color]
{{1},{2},{3}} => nema blokova sa uzastopnim brojevima pa {4} "dodajemo prazan skup" kako bismo dobili particiju {{1},{2},{3},{4}} tj. [color=blue][b]1-2-3-4[/b][/color]
Dakle, postupak ocito funkcionira, ali me muci kako da pokazem da ovaj postupak uspostavljanja bijekcije vrijedi za svaki [latex]n[/latex], tj. da za svaki [latex]n[/latex]-clani skup gornjim postupkom mozemo doci do stvarno [b]svih[/b] mogucih particija tog skupa u cijim blokovima nema uzastopnih brojeva? Kako mozemo biti sigurni da nismo preskocili jednu particiju sa tim svojstvom?
Drugim rijecima, ako pokazujemo bijektivnost preslikavanja, pa posebno i surjektivnost, kako pokazati da je slika naseg preslikavanja cijela kodomena, tj. skup svih particija bez uzastopnih brojeva u blokovima? A druga stvar je jos pokazati injektivnost, da razlicite particije [latex](n-1)[/latex]-clanog skupa preslika u razlicite particije [latex]n[/latex]-clanog skupa...
Zahvaljujem :naklon:
| goc (napisa): | znaci radis ovakvo preslikavanje. ako u nekom clanu particije n-1 brojeva imas uzastopne, uzmes cijeli taj niz brojeva i iz njega izbacujes parne zdesna. znaci ako imas 1234 izbacis 1 i 3, ak imas 12345 izbacis 2 i 4 i tako dalje.. sve te brojeve koje si izbacio potrpas u jedan novi skup(clan) i tamo jos dodas broj n. tada je to particija n brojeva takva da nema susjednih u istom clanu particije.. sad jos treba pokazat da je takvo preslikavanje bijektivno, to dalje nastavi  |
E, upravo me muci kako pokazati da je opisano preslikavanje stvarno bijekcija, koja "pokupi" bas sve particije sa trazenim svojstvom. Bio bih jako zahvalan za neki hint, smjernicu...
Pokusao sam raspisati:
Znamo da je 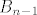 broj svih particija broj svih particija  -clanog skupa. Ako je taj broj jednak broju svih particija -clanog skupa. Ako je taj broj jednak broju svih particija  -clanog skupa koje imaju svojstvo da se ni u jednom bloku particije ne nalaze dva susjedna broja, onda mozemo uspostaviti bijekciju izmedju -clanog skupa koje imaju svojstvo da se ni u jednom bloku particije ne nalaze dva susjedna broja, onda mozemo uspostaviti bijekciju izmedju
skupa koji se sastoji od svih particija  -clanog skupa i -clanog skupa i
skupa koji se sastoji od svih particija  -clanog skupa u cijim blokovima nema susjednih brojeva, -clanog skupa u cijim blokovima nema susjednih brojeva,
na sljedeci nacin:
ako imamo neku particiju  skupa skupa 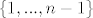 , oznacimo sa , oznacimo sa 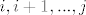 gdje je gdje je 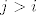 , maksimalno dugacak niz dva ili vise uzastopna broja u nekom bloku particije , maksimalno dugacak niz dva ili vise uzastopna broja u nekom bloku particije  . Iz ovako oznacenog niza izbacimo clanove . Iz ovako oznacenog niza izbacimo clanove 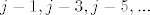 i ubacimo ih u skup i ubacimo ih u skup 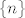 . Ovaj postupak ponovimo za sve nizove uzastopnih brojeva u particiji. . Ovaj postupak ponovimo za sve nizove uzastopnih brojeva u particiji.
Ocito je da uz  ne moze doci ne moze doci 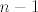 , jer uvijek biramo manji od dva uzastopna broja, odnosno ako se u nekome koraku u skupu koji sadrzi , jer uvijek biramo manji od dva uzastopna broja, odnosno ako se u nekome koraku u skupu koji sadrzi  i u koji ubacujemo brojeve nalazi neki i u koji ubacujemo brojeve nalazi neki  , uz njega ne mogu doci ni , uz njega ne mogu doci ni  (koji, kao veci broj, ostaje u svom skupu), ni (koji, kao veci broj, ostaje u svom skupu), ni 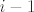 (jer njega ne ubacujemo u skup sa (jer njega ne ubacujemo u skup sa  jer se uz njega ne nalazi jer se uz njega ne nalazi  ). ).
Pogledajmo prvo, na primjeru skupa {1,2,3,4}, koje nam sve particije odgovaraju (particije bez uzastopnih brojeva u blokovima su zaplavljene):
[kraca oznaka: {{1,2,3},{4}} = 123-4]
1-2-3-4
12-3-4
13-2-4
14-2-3
23-1-4
24-1-3
34-1-2
123-4
124-3
134-2
234-1
12-34
13-24
14-23
1234
Mozemo li sve te zaplavljene particije dobiti gore opisanim postupkom?
Sve particije skupa {1,2,3} su:
{{1,2,3}} ⇒ ovdje imamo niz od tri uzastopna broja, izbacujemo (j-1)=2 i dodajemo ga u {4} kako bismo dobili particiju {{1,3},{2,4}} tj. 13-24
{{1,2},{3}} ⇒ iz prvog bloka izbacujemo 1 i stavljamo ga u {4} kako bismo dobili particiju {{2},{3},{1,4}} tj. 14-2-3
{{1,3},{2}} ⇒ nema blokova sa uzastopnim brojevima pa {4} "dodajemo prazan skup" kako bismo dobili particiju {{1,3},{2},{4}} tj. 13-2-4
{{2,3},{1}} ⇒ iz prvog bloka izbacujemo 2 i stavljamo ga u {4} kako bismo dobili particiju {{3},{1},{2,4}} tj. 24-1-3
{{1},{2},{3}} ⇒ nema blokova sa uzastopnim brojevima pa {4} "dodajemo prazan skup" kako bismo dobili particiju {{1},{2},{3},{4}} tj. 1-2-3-4
Dakle, postupak ocito funkcionira, ali me muci kako da pokazem da ovaj postupak uspostavljanja bijekcije vrijedi za svaki  , tj. da za svaki , tj. da za svaki  -clani skup gornjim postupkom mozemo doci do stvarno svih mogucih particija tog skupa u cijim blokovima nema uzastopnih brojeva? Kako mozemo biti sigurni da nismo preskocili jednu particiju sa tim svojstvom? -clani skup gornjim postupkom mozemo doci do stvarno svih mogucih particija tog skupa u cijim blokovima nema uzastopnih brojeva? Kako mozemo biti sigurni da nismo preskocili jednu particiju sa tim svojstvom?
Drugim rijecima, ako pokazujemo bijektivnost preslikavanja, pa posebno i surjektivnost, kako pokazati da je slika naseg preslikavanja cijela kodomena, tj. skup svih particija bez uzastopnih brojeva u blokovima? A druga stvar je jos pokazati injektivnost, da razlicite particije  -clanog skupa preslika u razlicite particije -clanog skupa preslika u razlicite particije  -clanog skupa... -clanog skupa...
Zahvaljujem 
_________________  |
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
|
| [Vrh] |
|
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
 Postano: 1:12 sub, 15. 11. 2008 Naslov: Postano: 1:12 sub, 15. 11. 2008 Naslov: |
    |
|
|
je li netko uspio rijesiti 7. a)?
pokazite da za Fibonaccijeve brojeve [latex]F_n[/latex] vrijedi
[latex]\sum_{i=0}^{\lfloor \frac{n-1}{2} \rfloor} F_{n-2i}=F_{n+1}-1[/latex], [latex]n \geq 1[/latex].
trebamo pokazati da ovo vrijedi za svaki [latex]n \geq 1[/latex], pa je valjda OK koristiti indukciju.
ali, baza za [latex]n=1[/latex] ne prolazi, jer [latex]\underbrace{F_1}_{=1} \neq \underbrace{F_2-1}_{=0} [/latex].
znaci da bi baza zapravo trebala biti za [latex]n=2[/latex]? (tada tvrdnja stima)
i drugo pitanje: ako pretpostavimo da za neki [latex]k \in \mathbb{N}[/latex] vrijedi
[latex]\sum_{i=0}^{\lfloor \frac{k-1}{2} \rfloor} F_{k-2i}=F_{k+1}-1[/latex], kako da pokazemo da vrijedi i
[latex]\sum_{i=0}^{\lfloor \frac{k}{2} \rfloor} F_{k+1-2i}=F_{k+2}-1[/latex]?
pokusavao sam raspisivati na razne nacine, ali iz toga nista korisno nije ispalo...
je li netko uspio rijesiti 7. a)?
pokazite da za Fibonaccijeve brojeve 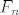 vrijedi vrijedi
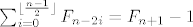 , , 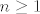 . .
trebamo pokazati da ovo vrijedi za svaki 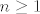 , pa je valjda OK koristiti indukciju. , pa je valjda OK koristiti indukciju.
ali, baza za 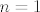 ne prolazi, jer ne prolazi, jer 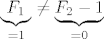 . .
znaci da bi baza zapravo trebala biti za  ? (tada tvrdnja stima) ? (tada tvrdnja stima)
i drugo pitanje: ako pretpostavimo da za neki 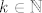 vrijedi vrijedi
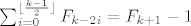 , kako da pokazemo da vrijedi i , kako da pokazemo da vrijedi i
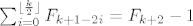 ? ?
pokusavao sam raspisivati na razne nacine, ali iz toga nista korisno nije ispalo...
_________________  |
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 5:38 sub, 15. 11. 2008 Naslov: Postano: 5:38 sub, 15. 11. 2008 Naslov: |
    |
|
|
[quote="gaston"]pokazite da za Fibonaccijeve brojeve [latex]F_n[/latex] vrijedi
[latex]\sum_{i=0}^{\lfloor \frac{n-1}{2} \rfloor} F_{n-2i}=F_{n+1}-1[/latex], [latex]n \geq 1[/latex].
[/quote]
Tu ne štima zapis. Nije svejedno da li je n paran ili neparan. Može se u Mathematici provjeriti:
[code:1]For[n = 1, n <= 50, n++,
Print[
{n,Sum[Fibonacci[n - 2 i], {i, 0, Floor[(n - 1)/2]}] == Fibonacci[n + 1],
Sum[Fibonacci[n - 2 i], {i, 0, Floor[(n - 1)/2]}] == Fibonacci[n + 1] - 1}
]
][/code:1]
[code:1]{1,True,False}
{2,False,True}
{3,True,False}
{4,False,True}
{5,True,False}
{6,False,True}
{7,True,False}
{8,False,True}
{9,True,False}
{10,False,True}
.
.
.
[/code:1]
Jednakost u zadatku vrijedi samo za parne n-ove. Ako se za nekoliko odabranih parnih n-ova raspiše suma, onda ispada da je to isto kao [latex]\sum_{i=0}^{n/2}F_{2i}[/latex] (vjerojatno se traži da se malo bolje obrazloži zašto je takav zapis isti kao i početni jer sve ostalo je trivić) pa se induktivno pokaže da vrijedi tvrdnja, tj.
[latex]F_2 + F_4 + \dots + F_n + F_{n+2}=F_{n+1}-1+F_{n+2}=F_{n+3}-1.[/latex]
Za neparne n-ove u jednadžbi nema -1 i analogno se sve pokazuje.
| gaston (napisa): | pokazite da za Fibonaccijeve brojeve 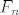 vrijedi vrijedi
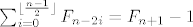 , , 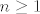 . .
|
Tu ne štima zapis. Nije svejedno da li je n paran ili neparan. Može se u Mathematici provjeriti:
| Kod: | For[n = 1, n <= 50, n++,
Print[
{n,Sum[Fibonacci[n - 2 i], {i, 0, Floor[(n - 1)/2]}] == Fibonacci[n + 1],
Sum[Fibonacci[n - 2 i], {i, 0, Floor[(n - 1)/2]}] == Fibonacci[n + 1] - 1}
]
] |
| Kod: | {1,True,False}
{2,False,True}
{3,True,False}
{4,False,True}
{5,True,False}
{6,False,True}
{7,True,False}
{8,False,True}
{9,True,False}
{10,False,True}
.
.
.
|
Jednakost u zadatku vrijedi samo za parne n-ove. Ako se za nekoliko odabranih parnih n-ova raspiše suma, onda ispada da je to isto kao 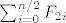 (vjerojatno se traži da se malo bolje obrazloži zašto je takav zapis isti kao i početni jer sve ostalo je trivić) pa se induktivno pokaže da vrijedi tvrdnja, tj. (vjerojatno se traži da se malo bolje obrazloži zašto je takav zapis isti kao i početni jer sve ostalo je trivić) pa se induktivno pokaže da vrijedi tvrdnja, tj.
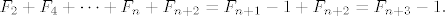
Za neparne n-ove u jednadžbi nema -1 i analogno se sve pokazuje.
_________________
The Dude Abides
|
|
| [Vrh] |
|
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
|
| [Vrh] |
|
shimija
Forumaš(ica)


Pridružen/a: 22. 01. 2007. (18:33:54)
Postovi: (138)16
Spol: 
Lokacija: Spljit
|
 Postano: 11:11 pon, 17. 11. 2008 Naslov: Postano: 11:11 pon, 17. 11. 2008 Naslov: |
    |
|
|
Ovo šta tebe zanima je ekvivalentno zapisu:
[latex]P_r^{n+1}=rP_{r-1}^n+rP_{r-1}^{n-1}+...+rP_{r-1}^r+rP_{r-1}^{r-1}[/latex]
Kako sad tumačit, najprije na neki način urediš skup(recimo pridjeliš elementima brojeve od 1 do n tako da postoji uređaj među njima). Na desnoj strani sad prvo uzmeš najveći element(možeš ga stavit na r načina) pa onda ostatak permutacije popuniš tako da samo gledaš elemente koji su manji od njega.
Npr. ako na početku odabereš element,tj. (n-k) onda ga staviš na r načina, a sad iz skupa {1,2,...,n-k-1} moraš uzeti (r-1) permutaciju
Ovo šta tebe zanima je ekvivalentno zapisu:
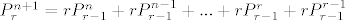
Kako sad tumačit, najprije na neki način urediš skup(recimo pridjeliš elementima brojeve od 1 do n tako da postoji uređaj među njima). Na desnoj strani sad prvo uzmeš najveći element(možeš ga stavit na r načina) pa onda ostatak permutacije popuniš tako da samo gledaš elemente koji su manji od njega.
Npr. ako na početku odabereš element,tj. (n-k) onda ga staviš na r načina, a sad iz skupa {1,2,...,n-k-1} moraš uzeti (r-1) permutaciju
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
 Postano: 12:37 pon, 17. 11. 2008 Naslov: Postano: 12:37 pon, 17. 11. 2008 Naslov: |
    |
|
|
[quote="gaston"]imam pitanje u vezi zadatka 2.d):
dokazite kombinatornim argumentom tvrdnju:
[latex]\sum_{k=0}^{n} 2^k \binom{n}{k} \binom{n-k}{\lfloor \frac{n-k}{2} \rfloor}=\binom{2n+1}{n}
[/latex]
na desnoj strani je [latex]\binom{2n+1}{n}[/latex] broj nacina na koji mozemo odabrati [latex]n[/latex]-clani podskup [latex](2n+1)[/latex]-clanog skupa, ali kako kombinatorno interpretirati lijevu stranu?
hvala[/quote]
2n+1 je n djecaka, n djevojcica grupiranih u n parova i jedan profesor od kojih n ide u kino. treba odabrat koji parovi ne idu cijeli, tko od para ide, koji idu cijeli, sto s profesorom...
| gaston (napisa): | imam pitanje u vezi zadatka 2.d):
dokazite kombinatornim argumentom tvrdnju:
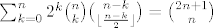
na desnoj strani je 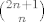 broj nacina na koji mozemo odabrati broj nacina na koji mozemo odabrati  -clani podskup -clani podskup 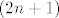 -clanog skupa, ali kako kombinatorno interpretirati lijevu stranu? -clanog skupa, ali kako kombinatorno interpretirati lijevu stranu?
hvala |
2n+1 je n djecaka, n djevojcica grupiranih u n parova i jedan profesor od kojih n ide u kino. treba odabrat koji parovi ne idu cijeli, tko od para ide, koji idu cijeli, sto s profesorom...
_________________  |
|
| [Vrh] |
|
betty
Forumaš(ica)
Pridružen/a: 23. 02. 2006. (19:17:18)
Postovi: (2D)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
Vip
Forumaš(ica)

Pridružen/a: 12. 10. 2007. (17:53:31)
Postovi: (8E)16
Spol: 
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
ivek imudaš
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: 
|
|
| [Vrh] |
|
|












