| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 18:02 sub, 22. 11. 2008 Naslov: Postano: 18:02 sub, 22. 11. 2008 Naslov: |
    |
|
|
[quote="Gino"][quote="goranm"]Taj izraz ne vrijedi za prvih 2 milijuna n (u Mathematici se lako provjeri).[/quote] sta ne vrijedi od 10 na dalje??[/quote]
Jok.
[code:1]For[n=10,n<=20,n++,
Print[
IntegerQ[(6^(2n)+19^n+2^(n+1))/17]
]
]
False
False
False
False
False
False
False
False
False
False
False[/code:1]
U gornjem kodu za n od 10 do 20 provjeravam da li je 6^(2n)+19^n+2^(n+1) pri dijeljenju sa 17 cijeli broj. Ako je, ispisat će se True, ako nije, ispisat će se False.
Ako se netko osobno želi uvjeriti u Mathematici, može probat:
[code:1]f[n_]:=6^(2n)+19^n+2^(n+1);
Monitor[For[n=1,n<=2000000,n++,If[IntegerQ[f[n]/17],Print[n]]],n][/code:1]
(po potrebi smanjiti 2 milijuna na neki manji broj ako je stroj slabiji)
| Gino (napisa): | | goranm (napisa): | | Taj izraz ne vrijedi za prvih 2 milijuna n (u Mathematici se lako provjeri). |
sta ne vrijedi od 10 na dalje?? |
Jok.
| Kod: | For[n=10,n<=20,n++,
Print[
IntegerQ[(6^(2n)+19^n+2^(n+1))/17]
]
]
False
False
False
False
False
False
False
False
False
False
False |
U gornjem kodu za n od 10 do 20 provjeravam da li je 6^(2n)+19^n+2^(n+1) pri dijeljenju sa 17 cijeli broj. Ako je, ispisat će se True, ako nije, ispisat će se False.
Ako se netko osobno želi uvjeriti u Mathematici, može probat:
| Kod: | f[n_]:=6^(2n)+19^n+2^(n+1);
Monitor[For[n=1,n<=2000000,n++,If[IntegerQ[f[n]/17],Print[n]]],n] |
(po potrebi smanjiti 2 milijuna na neki manji broj ako je stroj slabiji)
_________________
The Dude Abides
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:01 sub, 22. 11. 2008 Naslov: Postano: 19:01 sub, 22. 11. 2008 Naslov: |
    |
|
|
Izraz [latex]6^{2n} + 19^n + 2^{n+1}[/latex] nije djeljiv sa [latex]17[/latex] ni za koji [latex]n \in \mathbb{N} \cup \left\{ 0 \right\}[/latex]. Evo i dokaza...
Najprije ćemo pokazati da ako je [latex]a \equiv b \pmod{m}[/latex], onda je i [latex]a^n \equiv b^n \pmod{m}[/latex] za svaki nenegativan cijeli broj [latex]n[/latex], pri čemu su [latex]a[/latex] i [latex]b[/latex] cijeli, a [latex]m[/latex] prirodan broj. Ova tvrdnja slijedi direktno iz činjenice da je [latex]1 \equiv 1 \pmod{m}[/latex] i da je [latex]a^n - b^n = \left(a-b\right) \left(a^{n-1}+a^{n-2}b+ \ldots + ab^{n-2} + b^{n-1}\right)[/latex] za svaki prirodan broj [latex]n[/latex].
Sada imamo sljedeće
[latex]6^{2n} + 19^n + 2^{n+1} \equiv 36^n + 2^n + 2^{n+1} \equiv 2^n + 2^n + 2 \cdot 2^n \equiv 4 \cdot 2^n \equiv 2^{n+2} \pmod{17}[/latex].
Koristio sam da je [latex]19 \equiv 2 \pmod{17}[/latex] i [latex]36 \equiv 2 \pmod{17}[/latex].
Kada bi bilo [latex]6^{2n} + 19^n + 2^{n+1} \equiv 0 \pmod{17}[/latex], moralo bi biti [latex]2^{n+2} \equiv 0 \pmod{17}[/latex]. To je očito nemoguće jer je broj [latex]2^{n+2}[/latex] djeljiv jednim i samo jednim prostim brojem, brojem [latex]2[/latex] (on je potencija broja [latex]2[/latex]).
Izraz 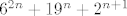 nije djeljiv sa nije djeljiv sa 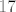 ni za koji ni za koji 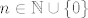 . Evo i dokaza... . Evo i dokaza...
Najprije ćemo pokazati da ako je 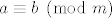 , onda je i , onda je i 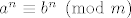 za svaki nenegativan cijeli broj za svaki nenegativan cijeli broj  , pri čemu su , pri čemu su  i i 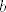 cijeli, a cijeli, a  prirodan broj. Ova tvrdnja slijedi direktno iz činjenice da je prirodan broj. Ova tvrdnja slijedi direktno iz činjenice da je 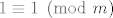 i da je i da je 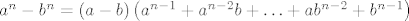 za svaki prirodan broj za svaki prirodan broj  . .
Sada imamo sljedeće
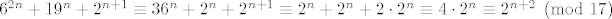 . .
Koristio sam da je 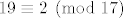 i i 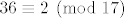 . .
Kada bi bilo 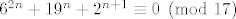 , moralo bi biti , moralo bi biti 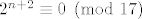 . To je očito nemoguće jer je broj . To je očito nemoguće jer je broj 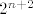 djeljiv jednim i samo jednim prostim brojem, brojem djeljiv jednim i samo jednim prostim brojem, brojem  (on je potencija broja (on je potencija broja  ). ).
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
 Postano: 14:17 ned, 23. 11. 2008 Naslov: Postano: 14:17 ned, 23. 11. 2008 Naslov: |
    |
|
|
ja sam se isto mučio naći bazu za taj zadatak :evil: :evil: djeljivo sa 17... a znam takve tipove riješit...a bez kalkulatora nemožeš ništa...probo sam lak i za n=5... izgubio sam 35 min na taj zadatak :evil: :evil: užasno...trebali bi paziti ubuduće kako zadaju...
[b]ja se nadam da će sada biti fer i korektni i nekako kompenzirati svima nama ovu pogrješku[/b] jer druge grupe nisu imale problema sa tim zadatkom...
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
[quote="JANKRI"]Izraz [latex]6^{2n} + 19^n + 2^{n+1}[/latex] nije djeljiv sa [latex]17[/latex] ni za koji [latex]n \in \mathbb{N} \cup \left\{ 0 \right\}[/latex]. Evo i dokaza...
Najprije ćemo pokazati da ako je [latex]a \equiv b \pmod{m}[/latex], onda je i [latex]a^n \equiv b^n \pmod{m}[/latex] za svaki nenegativan cijeli broj [latex]n[/latex], pri čemu su [latex]a[/latex] i [latex]b[/latex] cijeli, a [latex]m[/latex] prirodan broj. Ova tvrdnja slijedi direktno iz činjenice da je [latex]1 \equiv 1 \pmod{m}[/latex] i da je [latex]a^n - b^n = \left(a-b\right) \left(a^{n-1}+a^{n-2}b+ \ldots + ab^{n-2} + b^{n-1}\right)[/latex] za svaki prirodan broj [latex]n[/latex].
Sada imamo sljedeće
[latex]6^{2n} + 19^n + 2^{n+1} \equiv 36^n + 2^n + 2^{n+1} \equiv 2^n + 2^n + 2 \cdot 2^n \equiv 4 \cdot 2^n \equiv 2^{n+2} \pmod{17}[/latex].
Koristio sam da je [latex]19 \equiv 2 \pmod{17}[/latex] i [latex]36 \equiv 2 \pmod{17}[/latex].
Kada bi bilo [latex]6^{2n} + 19^n + 2^{n+1} \equiv 0 \pmod{17}[/latex], moralo bi biti [latex]2^{n+2} \equiv 0 \pmod{17}[/latex]. To je očito nemoguće jer je broj [latex]2^{n+2}[/latex] djeljiv jednim i samo jednim prostim brojem, brojem [latex]2[/latex] (on je potencija broja [latex]2[/latex]).[/quote]
Odlično riješeno:D no ja režem ruku ako je to ono što su oni mislili kada su zadavali taj zadatak...svi drugi su normalno mogli dokazat indukcijom...
ja sam se isto mučio naći bazu za taj zadatak   djeljivo sa 17... a znam takve tipove riješit...a bez kalkulatora nemožeš ništa...probo sam lak i za n=5... izgubio sam 35 min na taj zadatak djeljivo sa 17... a znam takve tipove riješit...a bez kalkulatora nemožeš ništa...probo sam lak i za n=5... izgubio sam 35 min na taj zadatak   užasno...trebali bi paziti ubuduće kako zadaju... užasno...trebali bi paziti ubuduće kako zadaju...
ja se nadam da će sada biti fer i korektni i nekako kompenzirati svima nama ovu pogrješku jer druge grupe nisu imale problema sa tim zadatkom...
Added after 1 minutes:
| JANKRI (napisa): | Izraz 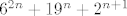 nije djeljiv sa nije djeljiv sa 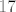 ni za koji ni za koji 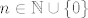 . Evo i dokaza... . Evo i dokaza...
Najprije ćemo pokazati da ako je 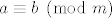 , onda je i , onda je i 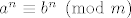 za svaki nenegativan cijeli broj za svaki nenegativan cijeli broj  , pri čemu su , pri čemu su  i i 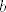 cijeli, a cijeli, a  prirodan broj. Ova tvrdnja slijedi direktno iz činjenice da je prirodan broj. Ova tvrdnja slijedi direktno iz činjenice da je 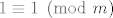 i da je i da je 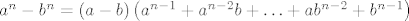 za svaki prirodan broj za svaki prirodan broj  . .
Sada imamo sljedeće
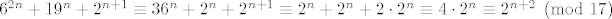 . .
Koristio sam da je 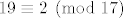 i i 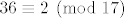 . .
Kada bi bilo 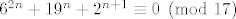 , moralo bi biti , moralo bi biti 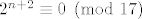 . To je očito nemoguće jer je broj . To je očito nemoguće jer je broj 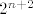 djeljiv jednim i samo jednim prostim brojem, brojem djeljiv jednim i samo jednim prostim brojem, brojem  (on je potencija broja (on je potencija broja  ). ). |
Odlično riješeno:D no ja režem ruku ako je to ono što su oni mislili kada su zadavali taj zadatak...svi drugi su normalno mogli dokazat indukcijom...
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
 Postano: 16:03 ned, 23. 11. 2008 Naslov: Postano: 16:03 ned, 23. 11. 2008 Naslov: |
    |
|
|
mislim da je par ljudi pitalo..u mojoj učionici par ljudi je pitalo a asistent im je odgovorio "to napišite u općenitom obliku i onda matematičkom indukcijom,a ako vrijedi za sve n onda vrijedi i za taj 2008."...i kaj smo mogli..pitali smo i nakon kolokvija i niš..mi smo svi znali da se to rješava tak,al kaj nam to vrijedi kad na pitanje dobiš odgovor koji ti ne odgovara na pitanje..
al dobro,bar smo sad to rješili..i sve će bit OK!
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
bilo bi bolje da su bar dva asistenta u prostoriji za vrijeme kolokvija..jer ako pozovemo asistenta da nam odgovori na neko pitanje,on mora pazit da ostali ne prepisuju i ne može se skoncentrirat na naše pitanje..
trebao bi bit jedan asistent iz tog kolegija,a drugi može bit neki iz bilo kojeg kolegija..tada bi se svi problemi mogli rješit na licu mjesta...
ali sve je to sad prošlost..problem je rješen!
mislim da je par ljudi pitalo..u mojoj učionici par ljudi je pitalo a asistent im je odgovorio "to napišite u općenitom obliku i onda matematičkom indukcijom,a ako vrijedi za sve n onda vrijedi i za taj 2008."...i kaj smo mogli..pitali smo i nakon kolokvija i niš..mi smo svi znali da se to rješava tak,al kaj nam to vrijedi kad na pitanje dobiš odgovor koji ti ne odgovara na pitanje..
al dobro,bar smo sad to rješili..i sve će bit OK!
Added after 4 minutes:
bilo bi bolje da su bar dva asistenta u prostoriji za vrijeme kolokvija..jer ako pozovemo asistenta da nam odgovori na neko pitanje,on mora pazit da ostali ne prepisuju i ne može se skoncentrirat na naše pitanje..
trebao bi bit jedan asistent iz tog kolegija,a drugi može bit neki iz bilo kojeg kolegija..tada bi se svi problemi mogli rješit na licu mjesta...
ali sve je to sad prošlost..problem je rješen!
|
|
| [Vrh] |
|
|


















