|
Na predavanju prof. Basraka imali smo primjer slučajnog pokusa koji se sastojao od bacanja dva novčića. Definirali smo tri proizvoljna skupa elementarnih događaja [latex]\Omega[/latex] i zanimala nas je vjerojatnost da se dogodi događaj [latex]A[/latex]={palo je bar jedno pismo}.
a) [latex]\Omega[/latex]={palo je bar jedno pismo, nije palo niti jedno pismo}
b) [latex]\Omega[/latex]={P i P , P i G , G i G}
c) [latex]\Omega[/latex]={(P,P),(P,G),(G,P),(G,G)}
Profesor je rekao da su sva tri izbora za [latex]\Omega[/latex] dobra, ali ako su novčići simetrični, prema Laplaceovom modelu (gdje se podrazumijeva da su svi elementarni događaji iz [latex]\Omega[/latex] jednako vjerojatni) za izbor [latex]\Omega[/latex] iz b) vrijedi [latex]P(A)=\frac{2}{3}[/latex], ali ako uzmemo [latex]\Omega[/latex] iz primjera c), što je isto dobar odabir, onda je [latex]P(A)=\frac{3}{4}[/latex].
:zbunjen:
Zanima me koja je na kraju vjerojatnost da, ako bacamo dva simetrična novčića, padne bar jedno pismo, tj. da se dogodi [latex]A[/latex] [color=gray](i možemo li u cijeloj priči uopće primijeniti Laplaceov model)[/color]?
Hvala :)
Na predavanju prof. Basraka imali smo primjer slučajnog pokusa koji se sastojao od bacanja dva novčića. Definirali smo tri proizvoljna skupa elementarnih događaja 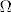 i zanimala nas je vjerojatnost da se dogodi događaj i zanimala nas je vjerojatnost da se dogodi događaj  ={palo je bar jedno pismo}. ={palo je bar jedno pismo}.
a) 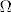 ={palo je bar jedno pismo, nije palo niti jedno pismo} ={palo je bar jedno pismo, nije palo niti jedno pismo}
b) 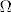 ={P i P , P i G , G i G} ={P i P , P i G , G i G}
c) 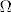 ={(P,P),(P,G),(G,P),(G,G)} ={(P,P),(P,G),(G,P),(G,G)}
Profesor je rekao da su sva tri izbora za 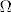 dobra, ali ako su novčići simetrični, prema Laplaceovom modelu (gdje se podrazumijeva da su svi elementarni događaji iz dobra, ali ako su novčići simetrični, prema Laplaceovom modelu (gdje se podrazumijeva da su svi elementarni događaji iz 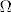 jednako vjerojatni) za izbor jednako vjerojatni) za izbor 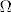 iz b) vrijedi iz b) vrijedi 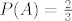 , ali ako uzmemo , ali ako uzmemo 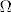 iz primjera c), što je isto dobar odabir, onda je iz primjera c), što je isto dobar odabir, onda je 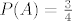 . .

Zanima me koja je na kraju vjerojatnost da, ako bacamo dva simetrična novčića, padne bar jedno pismo, tj. da se dogodi  (i možemo li u cijeloj priči uopće primijeniti Laplaceov model)? (i možemo li u cijeloj priči uopće primijeniti Laplaceov model)?
Hvala 
_________________  |





