| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
necka
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (20:09:04)
Postovi: (7)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:43 čet, 4. 12. 2008 Naslov: Postano: 14:43 čet, 4. 12. 2008 Naslov: |
    |
|
|
Mislim da ne... mi trebamo slučaj da je 1 adresa točna, 2 adrese točne, 3 adrese točne i sve adrese točne...
tu nam je lakše prebrojat komplement, dakle izračunat vjerojatnost da su sve adrese krive...
a tu nam treba silvesterova formula...
dakle, vjer da je bar 1 adresa dobra =
= 1 - ( 4*jedna kriva - 6*dvije krive + 4*tri krive - sve krive)
koliko se sjećam, bio je neki zadatak na vježbama iz vjerojatnosti sa šalicama i tanjurićima koji je išo na tu foru...
evo link:
[url=http://web.math.hr/nastava/uuv/files/vjezbe0708.pdf]Stranica 31, zadatak 3.13[/url]
Mislim da ne... mi trebamo slučaj da je 1 adresa točna, 2 adrese točne, 3 adrese točne i sve adrese točne...
tu nam je lakše prebrojat komplement, dakle izračunat vjerojatnost da su sve adrese krive...
a tu nam treba silvesterova formula...
dakle, vjer da je bar 1 adresa dobra =
= 1 - ( 4*jedna kriva - 6*dvije krive + 4*tri krive - sve krive)
koliko se sjećam, bio je neki zadatak na vježbama iz vjerojatnosti sa šalicama i tanjurićima koji je išo na tu foru...
evo link:
Stranica 31, zadatak 3.13
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
necka
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (20:09:04)
Postovi: (7)16
|
|
| [Vrh] |
|
goc
Forumaš(ica)

Pridružen/a: 18. 06. 2007. (12:13:18)
Postovi: (64)16
|
|
| [Vrh] |
|
Mr.Doe
Forumaš(ica)

Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
|
 Postano: 1:00 pet, 5. 12. 2008 Naslov: Postano: 1:00 pet, 5. 12. 2008 Naslov: |
    |
|
|
Ja cu napraviti samo za [latex]n=3[/latex], a tebi ostavljam opceniti slucaj ( analogan je ). Oznacimo sa p vjerojatnost da ce iz trece kutije biti izvucena bijela kuglica, tada imamo;
[latex]p=\underbrace{P(\textrm{izvucena je bijela kuglica u 3. kutiji}|\textrm{iz 2. kutije je izvucena bijela kuglica})}_{=\frac{a+1}{a+b+1}}*\newline
\underbrace{P(\textrm{iz 2. kutije je izvucena bijela })}_{p'}[/latex]
[latex] +\underbrace{P(\textrm{izvucena je bijela kuglica u 3. kutiji}|\textrm{iz 2. kutije je izvucena crna kuglica})}_{=\frac{a}{a+b+1}}*\newline
\underbrace{P(\textrm{iz 2. kutije je izvucena crna kuglica})}_{q'}[/latex],
sada nades vjerojatnost od p' (isto analogno ), a ona je jednaka;
[latex]p'=\frac{a+1}{a+b+1}\frac{a}{a+b}+\frac{a}{a+b+1}\frac{b}{a+b}[/latex], slicno i q'
[latex]q'=\frac{b+1}{a+b+1}\frac{b}{a+b}+\frac{b}{a+b+1}\frac{a}{a+b}[/latex],
sredi i dobijes traznu vjerojatnost.
Ima li tko ideju kako ovo elegantnije rijesiti?
Ja cu napraviti samo za 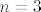 , a tebi ostavljam opceniti slucaj ( analogan je ). Oznacimo sa p vjerojatnost da ce iz trece kutije biti izvucena bijela kuglica, tada imamo; , a tebi ostavljam opceniti slucaj ( analogan je ). Oznacimo sa p vjerojatnost da ce iz trece kutije biti izvucena bijela kuglica, tada imamo;

 , ,
sada nades vjerojatnost od p' (isto analogno ), a ona je jednaka;
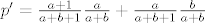 , slicno i q' , slicno i q'
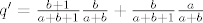 , ,
sredi i dobijes traznu vjerojatnost.
Ima li tko ideju kako ovo elegantnije rijesiti?
|
|
| [Vrh] |
|
Melkor
Forumaš(ica)


Pridružen/a: 07. 10. 2004. (18:48:00)
Postovi: (291)16
Spol: 
Lokacija: Void
|
 Postano: 2:45 pet, 5. 12. 2008 Naslov: Postano: 2:45 pet, 5. 12. 2008 Naslov: |
    |
|
|
Mr. Doe, to je to, samo treba stvari malo izokrenuti pa postane jasnije što se dogodi.
Uvedimo oznake: [latex]p_i[/latex] za vjerojatnost da je iz [latex]i[/latex]-te kutije izvučena bijela kuglica i analogno [latex]q_i[/latex] za crnu kuglicu.
Vrijedi: [latex]p_1=a/(a+b)[/latex] i [latex]q_1=b/(a+b)[/latex].
Osim toga, slijedeći ovo što je Mr. Doe napisao, imamo sljedeće rekurzivne relacije za [latex]i>1[/latex]:
[latex]
\begin{aligned}
p_{i} =\ & \frac{a+1}{a+b+1}\cdot p_{i-1} + \frac{a}{a+b+1}\cdot q_{i-1} \\
q_{i} =\ &\frac{b}{a+b+1}\cdot p_{i-1} + \frac{b+1}{a+b+1}\cdot q_{i-1}
\end{aligned}
[/latex]
To se elegantnije može zapisati matrično:
[latex]
\begin{bmatrix}
p_i \\
q_i
\end{bmatrix}
=
\begin{bmatrix}
\frac{a+1}{a+b+1} & \frac{a}{a+b+1} \\
\frac{b}{a+b+1} & \frac{b+1}{a+b+1}
\end{bmatrix}
\begin{bmatrix}
p_{i-1} \\
q_{i-1}
\end{bmatrix}
=
\begin{bmatrix}
\frac{a+1}{a+b+1} & \frac{a}{a+b+1} \\
\frac{b}{a+b+1} & \frac{b+1}{a+b+1}
\end{bmatrix}^{i-1}
\begin{bmatrix}
p_1 \\
q_1
\end{bmatrix}
[/latex]
Ali, umjesto da se računa potencija te matrice, stvar je vrlo jednostavna kad se uvrste početni uvjeti. Naime, sređivanjem se lako dobije da je
[latex]\displaystyle p_2=\frac{a}{a+b},\qquad q_2=\frac{b}{a+b}\,.[/latex]
Induktivno je onda za svaki [latex]i[/latex]:
[latex]\displaystyle p_i=\frac{a}{a+b},\qquad q_i=\frac{b}{a+b}\,.[/latex]
Drugim riječima, vjerojatnost da će iz [latex]n[/latex]-te kutije biti izvučena bijela kuglica je ista kao što bi bila bez svih ovih prebacivanja kuglica. Fora. :)
Mr. Doe, to je to, samo treba stvari malo izokrenuti pa postane jasnije što se dogodi.
Uvedimo oznake: 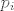 za vjerojatnost da je iz za vjerojatnost da je iz  -te kutije izvučena bijela kuglica i analogno -te kutije izvučena bijela kuglica i analogno 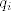 za crnu kuglicu. za crnu kuglicu.
Vrijedi: 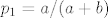 i i 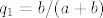 . .
Osim toga, slijedeći ovo što je Mr. Doe napisao, imamo sljedeće rekurzivne relacije za 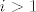 : :
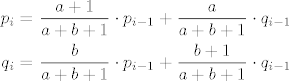
To se elegantnije može zapisati matrično:
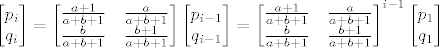
Ali, umjesto da se računa potencija te matrice, stvar je vrlo jednostavna kad se uvrste početni uvjeti. Naime, sređivanjem se lako dobije da je

Induktivno je onda za svaki  : :

Drugim riječima, vjerojatnost da će iz  -te kutije biti izvučena bijela kuglica je ista kao što bi bila bez svih ovih prebacivanja kuglica. Fora. -te kutije biti izvučena bijela kuglica je ista kao što bi bila bez svih ovih prebacivanja kuglica. Fora. 
_________________
I don't know half of you half as well as I should like; and I like less than half of you half as well as you deserve.
|
|
| [Vrh] |
|
necka
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (20:09:04)
Postovi: (7)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
|






