| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
xsssx
Forumaš(ica)

Pridružen/a: 04. 01. 2009. (15:37:11)
Postovi: (1)16
|
 Postano: 15:56 ned, 4. 1. 2009 Naslov: Nizovi, funkcije, limesi i asimptote? Postano: 15:56 ned, 4. 1. 2009 Naslov: Nizovi, funkcije, limesi i asimptote? |
    |
|
|
molim vas odgovor na pitanja, treba mi relativno brzo:
1) niz cija su gomilista svi prirodni brojevi
2)primjer funkcije, definirana u 0, ali limes u 0 je +beskonacno
3) sljedeci limes rjesiti BEZ L'hospitala: lim(y ide u beskonacno) od: pod korijenom(korijen(1+y) + 1) - pod korijenom(korijen(1+y*y) + y) ili ako je lakse sqrt(sqrt(1+y) + 1) - sqrt(sqrt(1+y*y) + y)
4) primjer funkcije koja ima limes slijeva u 0= - beskonacno, limes zdesna u 0=1
5)primjer funkcije koja nije definirana u 0, ima limes u 0
i primjer funkcije koja je definirana u 0 ali nema limes u 0
6)primjer funkcije sa 2 razlicite kose asimptote
molim vas odgovor na pitanja, treba mi relativno brzo:
1) niz cija su gomilista svi prirodni brojevi
2)primjer funkcije, definirana u 0, ali limes u 0 je +beskonacno
3) sljedeci limes rjesiti BEZ L'hospitala: lim(y ide u beskonacno) od: pod korijenom(korijen(1+y) + 1) - pod korijenom(korijen(1+y*y) + y) ili ako je lakse sqrt(sqrt(1+y) + 1) - sqrt(sqrt(1+y*y) + y)
4) primjer funkcije koja ima limes slijeva u 0= - beskonacno, limes zdesna u 0=1
5)primjer funkcije koja nije definirana u 0, ima limes u 0
i primjer funkcije koja je definirana u 0 ali nema limes u 0
6)primjer funkcije sa 2 razlicite kose asimptote
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 22:06 ned, 4. 1. 2009 Naslov: Re: pitanja, pliz hitno Postano: 22:06 ned, 4. 1. 2009 Naslov: Re: pitanja, pliz hitno |
    |
|
|
[quote="xsssx"]1) niz cija su gomilista svi prirodni brojevi[/quote]
1, 1,2, 1,2,3, 1,2,3,4, 1,2,3,4,5, ....
pa kome se da nek izvede opći član.
[quote="xsssx"]2)primjer funkcije, definirana u 0, ali limes u 0 je +beskonacno[/quote]
[latex]f(x):=\begin{cases} \frac{1}{x^{2}} & x\neq 0 \\ 6 & x=0 \end{cases}[/latex]
Slično tako ništimaš one ostale funkcije.
| xsssx (napisa): | | 1) niz cija su gomilista svi prirodni brojevi |
1, 1,2, 1,2,3, 1,2,3,4, 1,2,3,4,5, ....
pa kome se da nek izvede opći član.
| xsssx (napisa): | | 2)primjer funkcije, definirana u 0, ali limes u 0 je +beskonacno |
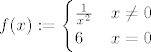
Slično tako ništimaš one ostale funkcije.
Zadnja promjena: rafaelm; 22:16 ned, 4. 1. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:15 ned, 4. 1. 2009 Naslov: Re: pitanja, pliz hitno Postano: 22:15 ned, 4. 1. 2009 Naslov: Re: pitanja, pliz hitno |
    |
|
|
[quote="xsssx"]
2)primjer funkcije, definirana u 0, ali limes u 0 je +beskonacno
3) sljedeci limes rjesiti BEZ L'hospitala: lim(y ide u beskonacno) od: pod korijenom(korijen(1+y) + 1) - pod korijenom(korijen(1+y*y) + y) ili ako je lakse sqrt(sqrt(1+y) + 1) - sqrt(sqrt(1+y*y) + y)
4) primjer funkcije koja ima limes slijeva u 0= - beskonacno, limes zdesna u 0=1
5)primjer funkcije koja nije definirana u 0, ima limes u 0
i primjer funkcije koja je definirana u 0 ali nema limes u 0
6)primjer funkcije sa 2 razlicite kose asimptote[/quote]
2) f(x) = { 1/x , x!=0
[color=white].................[/color]5, x==0
3)L'Hospital je deriviranje brojnika i nazivnika. Ovdje se može "racionalizirati" brojnik ( pomnožit sa (korijen + korijen) / (korijen + korijen) ) i onda podijelit sa najvećom potencijom
4) f(x) = { -1/x , x<0
[color=white].................[/color]1, x>=0
5) f(x) = sinx/x nije def a ima limes
@ Milojko Elipsa nije fja. :D
| xsssx (napisa): |
2)primjer funkcije, definirana u 0, ali limes u 0 je +beskonacno
3) sljedeci limes rjesiti BEZ L'hospitala: lim(y ide u beskonacno) od: pod korijenom(korijen(1+y) + 1) - pod korijenom(korijen(1+y*y) + y) ili ako je lakse sqrt(sqrt(1+y) + 1) - sqrt(sqrt(1+y*y) + y)
4) primjer funkcije koja ima limes slijeva u 0= - beskonacno, limes zdesna u 0=1
5)primjer funkcije koja nije definirana u 0, ima limes u 0
i primjer funkcije koja je definirana u 0 ali nema limes u 0
6)primjer funkcije sa 2 razlicite kose asimptote |
2) f(x) = { 1/x , x!=0
.................5, x==0
3)L'Hospital je deriviranje brojnika i nazivnika. Ovdje se može "racionalizirati" brojnik ( pomnožit sa (korijen + korijen) / (korijen + korijen) ) i onda podijelit sa najvećom potencijom
4) f(x) = { -1/x , x<0
.................1, x>=0
5) f(x) = sinx/x nije def a ima limes
@ Milojko Elipsa nije fja. 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:46 ned, 4. 1. 2009 Naslov: Re: pitanja, pliz hitno Postano: 22:46 ned, 4. 1. 2009 Naslov: Re: pitanja, pliz hitno |
    |
|
|
[quote="rafaelm"][quote="Luuka"]2) f(x) = { 1/x , x!=0
.................5, x==0
[/quote]
Ova funkcija nema limes u nuli. limes slijeva je [latex]-\infty[/latex], a s desna [latex]+\infty[/latex][/quote]
Opla... tnx... onda neka bude
f(x) = { 1/x , x>0
[color=white]............[/color]-1/x , x<0
[color=white]............[/color]5, x==0
[size=9][color=#999999]Added after 20 minutes:[/color][/size]
[quote="xsssx"]
6)primjer funkcije sa 2 razlicite kose asimptote[/quote]
Uzmemo hiperbolu, ali samo njen dio iznad x-osi... (y>=0 jer onda je to fja). Ako je x^2/a^2 - y^2/b^2=1 hiperbola onda definiramo
[latex]f(x) = \sqrt{ b^2 \cdot ( \frac{x^2}{a^2} - 1 )}[/latex]
Ta fja ima dvije različite kose asimptote ( one od hiperbole )
| rafaelm (napisa): | | Luuka (napisa): | 2) f(x) = { 1/x , x!=0
.................5, x==0
|
Ova funkcija nema limes u nuli. limes slijeva je 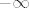 , a s desna , a s desna  |
Opla... tnx... onda neka bude
f(x) = { 1/x , x>0
............-1/x , x<0
............5, x==0
Added after 20 minutes:
| xsssx (napisa): |
6)primjer funkcije sa 2 razlicite kose asimptote |
Uzmemo hiperbolu, ali samo njen dio iznad x-osi... (y>=0 jer onda je to fja). Ako je x^2/a^2 - y^2/b^2=1 hiperbola onda definiramo
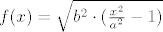
Ta fja ima dvije različite kose asimptote ( one od hiperbole )
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
|










