| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
 Postano: 18:05 pon, 5. 1. 2009 Naslov: Pomoc oko 2 zadatka. Postano: 18:05 pon, 5. 1. 2009 Naslov: Pomoc oko 2 zadatka. |
    |
|
|
1.U igri igrač baci 4 novčića i osvaja 2 boda za pismo i -1 bod za glavu u ishodu bacanja. Za slučajnu varijablu zadanu kao broj bodova koje osvoji odredi: razdiobu i funkciju razdiobe.
2.Odredi vjerojatnost da se u 300 bacanja kocke broj 4 pojavi 40 puta.(to znam-aproksimiram normalnom razdiobom). Koliko najviše a koliko najmanje ponavljanja broja 4 je realno očekivati u tih 300 bacanja? - To ne kužim, da li samo koristim onu 3sigma pravilo (u-3*sigma,u+3*sigma), bilo mi je čudno jer sam negdje vidio da je napisano (u-2*sigma,u+2*sigma) ili (u-sigma,u+sigma) za takav zadatak.
Puno vam hvala na pomoći!
1.U igri igrač baci 4 novčića i osvaja 2 boda za pismo i -1 bod za glavu u ishodu bacanja. Za slučajnu varijablu zadanu kao broj bodova koje osvoji odredi: razdiobu i funkciju razdiobe.
2.Odredi vjerojatnost da se u 300 bacanja kocke broj 4 pojavi 40 puta.(to znam-aproksimiram normalnom razdiobom). Koliko najviše a koliko najmanje ponavljanja broja 4 je realno očekivati u tih 300 bacanja? - To ne kužim, da li samo koristim onu 3sigma pravilo (u-3*sigma,u+3*sigma), bilo mi je čudno jer sam negdje vidio da je napisano (u-2*sigma,u+2*sigma) ili (u-sigma,u+sigma) za takav zadatak.
Puno vam hvala na pomoći!
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
 Postano: 20:26 pon, 5. 1. 2009 Naslov: Re: Pomoc oko 2 zadatka. Postano: 20:26 pon, 5. 1. 2009 Naslov: Re: Pomoc oko 2 zadatka. |
    |
|
|
[quote="baky0905"]1.U igri igrač baci 4 novčića i osvaja 2 boda za pismo i -1 bod za glavu u ishodu bacanja. Za slučajnu varijablu zadanu kao broj bodova koje osvoji odredi: razdiobu i funkciju razdiobe.
[/quote]
Gledaj jedna novcic, i napisi distribuciju te slucajne varijable. Ona je ( surprise, surprise ) transformirana Bernulijeva slucajna varijabla, pa je suma tih 4 sl.var transformirana binomna sl.varijabla. Evo vec rekao sam ti njenu distribuciju, samo moras naci koje vrijednosti ona poprima.
[quote="baky0905"]
...je realno očekivati u tih...
[/quote]
Ovo nista ne znaci :roll:. Inace za ovako nesta kod nas padas na usmenom, u najmanju ruku te profesor cudno gleda.
Kladim se u rucak u menzi, da si to dobio za zadacu ( pucam na ekonomiju/strojarstvo/fer ), i moras je predati u srijedu, pa si mislio zasto se muciti sa ovako jednostavnim zadacima, neka mi ih matematicari rijese [size=7]oni ionako nista pametno ne rade[/size]. Jesam li u pravu? :lol:
| baky0905 (napisa): | 1.U igri igrač baci 4 novčića i osvaja 2 boda za pismo i -1 bod za glavu u ishodu bacanja. Za slučajnu varijablu zadanu kao broj bodova koje osvoji odredi: razdiobu i funkciju razdiobe.
|
Gledaj jedna novcic, i napisi distribuciju te slucajne varijable. Ona je ( surprise, surprise ) transformirana Bernulijeva slucajna varijabla, pa je suma tih 4 sl.var transformirana binomna sl.varijabla. Evo vec rekao sam ti njenu distribuciju, samo moras naci koje vrijednosti ona poprima.
| baky0905 (napisa): |
...je realno očekivati u tih...
|
Ovo nista ne znaci  . Inace za ovako nesta kod nas padas na usmenom, u najmanju ruku te profesor cudno gleda. . Inace za ovako nesta kod nas padas na usmenom, u najmanju ruku te profesor cudno gleda.
Kladim se u rucak u menzi, da si to dobio za zadacu ( pucam na ekonomiju/strojarstvo/fer ), i moras je predati u srijedu, pa si mislio zasto se muciti sa ovako jednostavnim zadacima, neka mi ih matematicari rijese oni ionako nista pametno ne rade. Jesam li u pravu? 
|
|
| [Vrh] |
|
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
 Postano: 21:06 pon, 5. 1. 2009 Naslov: Postano: 21:06 pon, 5. 1. 2009 Naslov: |
    |
|
|
Ma prijatelju neces dobiti matematicare sa ruckom, trebas im dati cevape :pc: ( i to one prave iz Rubelja )!
Dakle, neka su Bernulijeve sl. varijable [latex]X_1,\dots,X_4[/latex], dakle one poprimaju vrijednosti 0 i 1, sa jednakom vjerojatnoscu. Pogledaj slucajnu varijablu [latex]3X_i-1[/latex], ona poprima vrijednosti -1 i 2 ( dakle ono sto ti trebas ) sa jednakom vjerojatnoscu. Sada sumiras te 4 slu. varijable, dobijes [latex]3X_1-1+\dots 3X_4-1=3(X_1+\dots+X_4)-4[/latex]. [latex]X_1+\dots+X_4[/latex] poprima vrijednosti u skupu [latex]\{0,1,\dots,4\}[/latex] pa [latex]3(X_1+\dots+X_4)[/latex] poprima vrijednosti u skupu [latex]\{0,3,6,9,12\}[/latex], sada im oduzmes vrijednost 4, pa ono sto ti trebas poprima vrijednosti u skupu [latex]\{-4,-1,2,5,8\}[/latex]. Sada jos trebas vjerojatnosti, ponovno se vratis na [latex]X_1+\dots+X_4[/latex], vjerojatnosti su dane na sljedeci nacin [latex]\mathbb{P}(X_1+\dots+X_4=i)={4\choose i}\big(\frac{1}{2}\big)^4,i=0,\dots 4 [/latex]. To sto si kasnije transformirao te sl.varijable uopce ne utjece na vjerojatnosti.
Puno srece na kolokviju i neka bude petica!!!
Ma prijatelju neces dobiti matematicare sa ruckom, trebas im dati cevape  ( i to one prave iz Rubelja )! ( i to one prave iz Rubelja )!
Dakle, neka su Bernulijeve sl. varijable  , dakle one poprimaju vrijednosti 0 i 1, sa jednakom vjerojatnoscu. Pogledaj slucajnu varijablu , dakle one poprimaju vrijednosti 0 i 1, sa jednakom vjerojatnoscu. Pogledaj slucajnu varijablu 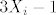 , ona poprima vrijednosti -1 i 2 ( dakle ono sto ti trebas ) sa jednakom vjerojatnoscu. Sada sumiras te 4 slu. varijable, dobijes , ona poprima vrijednosti -1 i 2 ( dakle ono sto ti trebas ) sa jednakom vjerojatnoscu. Sada sumiras te 4 slu. varijable, dobijes 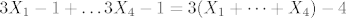 . . 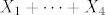 poprima vrijednosti u skupu poprima vrijednosti u skupu 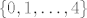 pa pa  poprima vrijednosti u skupu poprima vrijednosti u skupu 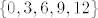 , sada im oduzmes vrijednost 4, pa ono sto ti trebas poprima vrijednosti u skupu , sada im oduzmes vrijednost 4, pa ono sto ti trebas poprima vrijednosti u skupu 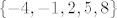 . Sada jos trebas vjerojatnosti, ponovno se vratis na . Sada jos trebas vjerojatnosti, ponovno se vratis na 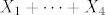 , vjerojatnosti su dane na sljedeci nacin , vjerojatnosti su dane na sljedeci nacin 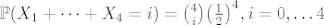 . To sto si kasnije transformirao te sl.varijable uopce ne utjece na vjerojatnosti. . To sto si kasnije transformirao te sl.varijable uopce ne utjece na vjerojatnosti.
Puno srece na kolokviju i neka bude petica!!!
|
|
| [Vrh] |
|
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
 Postano: 22:43 pon, 5. 1. 2009 Naslov: Postano: 22:43 pon, 5. 1. 2009 Naslov: |
    |
|
|
Sori na gnjavaži, samo me zanima kako smo došli do te slučajne varijable 3*Xi-1 koja baš prima te vrijedonosti 2 i -1... Našao sam negdje da je netko napisao za ovaj zadatak razdiobu Z=5*X-4.
Z-sl. var. koja broji bacanja, X-broj pisama.
Ja ti ne znam baš puno iz vjerojatnosti. Muči me to što nismo ni jedan zadatak imali sa postavljanjem razdiobi, a rješavali smo binomne, poissonove i normalne raz i onda nam u kolokviju da da napravimo razdiobu:) Sigurno misliš da imam neka debila pitanja (a i imam:) )
Ali nekako moram naučiti, pa ako ne pitam neću nikad dobiti odgovor:)
I jel ono onda dobro kada tražim raspon najmanjeg i najvećeg ponavljanja broja 4 - (u-3*sigma, u+3*sigma) ?
Baš mi je drago da netko hoće pomoći.
Hvala još jednom.
Sori na gnjavaži, samo me zanima kako smo došli do te slučajne varijable 3*Xi-1 koja baš prima te vrijedonosti 2 i -1... Našao sam negdje da je netko napisao za ovaj zadatak razdiobu Z=5*X-4.
Z-sl. var. koja broji bacanja, X-broj pisama.
Ja ti ne znam baš puno iz vjerojatnosti. Muči me to što nismo ni jedan zadatak imali sa postavljanjem razdiobi, a rješavali smo binomne, poissonove i normalne raz i onda nam u kolokviju da da napravimo razdiobu:) Sigurno misliš da imam neka debila pitanja (a i imam:) )
Ali nekako moram naučiti, pa ako ne pitam neću nikad dobiti odgovor:)
I jel ono onda dobro kada tražim raspon najmanjeg i najvećeg ponavljanja broja 4 - (u-3*sigma, u+3*sigma) ?
Baš mi je drago da netko hoće pomoći.
Hvala još jednom.
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
 Postano: 23:53 pon, 5. 1. 2009 Naslov: Postano: 23:53 pon, 5. 1. 2009 Naslov: |
    |
|
|
[quote="baky0905"]Sori na gnjavaži, samo me zanima kako smo došli do te slučajne varijable 3*Xi-1 koja baš prima te vrijedonosti 2 i -1... Našao sam negdje da je netko napisao za ovaj zadatak razdiobu Z=5*X-4.
Z-sl. var. koja broji bacanja, X-broj pisama.[/quote]
Sigurno nije napisao [latex]Z=5\cdot X-4[/latex], pretpostavi da je bilo 2 pisma, onda bi trebao dobiti 6 boda, a to nije u skladu sa zadatkom, naime ako je bilo 2 pisma onda treba dobiti 2 boda ( provjeri to ). Dakle, treba biti [latex]Z=3\cdot X-4[/latex], gdje su Z i X kao sto si naveo. Ako malo bolje pogledas to je upravo ono sto sam ja napisao, samo sto sam ja "gradio" slucajnu varijablu Z ispocetka. Naime, broj pisama ( kod tebe X ) nije nista drugo nego [latex]X_1+\dots+X_4[/latex] ( dakle u svakom bacanju gledas da li je palo pismo, i u tom slucaju pridodas jedinicu, ono uspjeh u tom bacanju, i te fore ).
E sad, kako sam dosao do [latex]3X_i-1[/latex]?! Samo sam trazio slucajnu varijablu koja poprima dvije vrijednosti i da su te dvije vrijednosti su -1 i 2. Nista specijalno, samo se treba malo snaci. A buduci da su Bernulijeve sl.varijable najjednostavnije ( i najvaznije! ), isao sam njih transformirati.
[quote="baky0905"]
I jel ono onda dobro kada tražim raspon najmanjeg i najvećeg ponavljanja broja 4 - (u-3*sigma, u+3*sigma) ?
[/quote]
Kao sto rekoh, prvi put cujem za termin "realno", bolje da to pitas ekipu sa svojeg faksa. Ako netko zna sta to znaci neka gukne!
| baky0905 (napisa): | Sori na gnjavaži, samo me zanima kako smo došli do te slučajne varijable 3*Xi-1 koja baš prima te vrijedonosti 2 i -1... Našao sam negdje da je netko napisao za ovaj zadatak razdiobu Z=5*X-4.
Z-sl. var. koja broji bacanja, X-broj pisama. |
Sigurno nije napisao 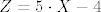 , pretpostavi da je bilo 2 pisma, onda bi trebao dobiti 6 boda, a to nije u skladu sa zadatkom, naime ako je bilo 2 pisma onda treba dobiti 2 boda ( provjeri to ). Dakle, treba biti , pretpostavi da je bilo 2 pisma, onda bi trebao dobiti 6 boda, a to nije u skladu sa zadatkom, naime ako je bilo 2 pisma onda treba dobiti 2 boda ( provjeri to ). Dakle, treba biti 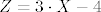 , gdje su Z i X kao sto si naveo. Ako malo bolje pogledas to je upravo ono sto sam ja napisao, samo sto sam ja "gradio" slucajnu varijablu Z ispocetka. Naime, broj pisama ( kod tebe X ) nije nista drugo nego , gdje su Z i X kao sto si naveo. Ako malo bolje pogledas to je upravo ono sto sam ja napisao, samo sto sam ja "gradio" slucajnu varijablu Z ispocetka. Naime, broj pisama ( kod tebe X ) nije nista drugo nego 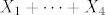 ( dakle u svakom bacanju gledas da li je palo pismo, i u tom slucaju pridodas jedinicu, ono uspjeh u tom bacanju, i te fore ). ( dakle u svakom bacanju gledas da li je palo pismo, i u tom slucaju pridodas jedinicu, ono uspjeh u tom bacanju, i te fore ).
E sad, kako sam dosao do 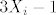 ?! Samo sam trazio slucajnu varijablu koja poprima dvije vrijednosti i da su te dvije vrijednosti su -1 i 2. Nista specijalno, samo se treba malo snaci. A buduci da su Bernulijeve sl.varijable najjednostavnije ( i najvaznije! ), isao sam njih transformirati. ?! Samo sam trazio slucajnu varijablu koja poprima dvije vrijednosti i da su te dvije vrijednosti su -1 i 2. Nista specijalno, samo se treba malo snaci. A buduci da su Bernulijeve sl.varijable najjednostavnije ( i najvaznije! ), isao sam njih transformirati.
| baky0905 (napisa): |
I jel ono onda dobro kada tražim raspon najmanjeg i najvećeg ponavljanja broja 4 - (u-3*sigma, u+3*sigma) ?
|
Kao sto rekoh, prvi put cujem za termin "realno", bolje da to pitas ekipu sa svojeg faksa. Ako netko zna sta to znaci neka gukne!
|
|
| [Vrh] |
|
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
|
| [Vrh] |
|
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
|
| [Vrh] |
|
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
 Postano: 19:41 pet, 9. 1. 2009 Naslov: Postano: 19:41 pet, 9. 1. 2009 Naslov: |
    |
|
|
Oznacimo sa [latex]X_1,X_2[/latex] slucajne varijable koje ce respektivno, oznacavati bacanje 1, odnosno 2 ( simetricne ) kocke. Njihova distribucija je sljedeca;
[latex]X_i\sim \left(\begin{array}{ccc}
1 & \dots & 6 \\
\frac{1}{6} & \dots & \frac{1}{6} \\
\end{array}\right), i=1,2[/latex]. Pogledajmo prvo razliku ishoda bacanja te dvije kocke, tj pogledajmo koje vrijednosti mogu poprimiti, ocigledno je ( provjeri ) [latex]\big( X_1-X_2 \big)(\Omega)=\{-5,\dots, 5\}[/latex]. Treba jos samo odrediti vjerojatnosti, i to vjerojatnosti da [latex]X_1-X_2[/latex] poprimi vrijednosti [latex]-5,\dots,0[/latex] jer ostale vrijednosti ide po analogiji. Dakle, sljedece su oznake [latex](i,j)[/latex] znaci da je na prvoj koci pao broj i a na kocki 2 broj j.
[latex]X_1-X_2[/latex] moze poprimiti vrijednost -5 samo ako je [latex](1,6)[/latex], vrijednost -4 samo ako je [latex](2,6),(1,5)[/latex], vrijednost -3 samo ako je [latex](3,6),(2,5),(1,4)[/latex], vrijednost -2 samo ako je [latex](4,6),(3,5),(2,4),(1,3)[/latex], vrijednost -1 samo ako je [latex](5,6),(4,5),(3,4),(2,3),(1,2)[/latex], te vrijednost 0 samo ako je [latex](i,i), i=1,\dots 6[/latex]. Vrijednosti 1,...,5 idu po analogiji, samo vrijednost [latex](i,j)[/latex] zamijenis sa [latex](j,i)[/latex]. Sada jos samo treba naci vjerojatnost [latex]\mathbb{P}(X_1=i,X_2=j)[/latex], no buduci da se kocke bacaju nezavisno ( inace ovo nista ne ide ), ta vjerojatnost je ocigledno 1/36. Napisimo sada razdiobu od X_1-X_2
[latex]X_1-X_2\sim \left(\begin{array}{ccccccccccc}
- 5 & -4 & -3 & -2 & -1 & 0 & 1 & 2 & 3 & 4 & 5 \\
\frac{1}{36} & \frac{2}{36} & \frac{3}{36} & \frac{4}{36} & \frac{5}{36} & \frac{6}{36} & \frac{5}{36} & \frac{4}{36} & \frac{3}{36} & \frac{2}{36} & \frac{1}{36} \\
\end{array}\right) [/latex].
Zadatak necu zavrsiti jer cevape nisam dobio!!!!
Oznacimo sa 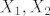 slucajne varijable koje ce respektivno, oznacavati bacanje 1, odnosno 2 ( simetricne ) kocke. Njihova distribucija je sljedeca; slucajne varijable koje ce respektivno, oznacavati bacanje 1, odnosno 2 ( simetricne ) kocke. Njihova distribucija je sljedeca;
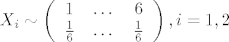 . Pogledajmo prvo razliku ishoda bacanja te dvije kocke, tj pogledajmo koje vrijednosti mogu poprimiti, ocigledno je ( provjeri ) . Pogledajmo prvo razliku ishoda bacanja te dvije kocke, tj pogledajmo koje vrijednosti mogu poprimiti, ocigledno je ( provjeri ) 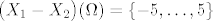 . Treba jos samo odrediti vjerojatnosti, i to vjerojatnosti da . Treba jos samo odrediti vjerojatnosti, i to vjerojatnosti da  poprimi vrijednosti poprimi vrijednosti  jer ostale vrijednosti ide po analogiji. Dakle, sljedece su oznake jer ostale vrijednosti ide po analogiji. Dakle, sljedece su oznake 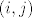 znaci da je na prvoj koci pao broj i a na kocki 2 broj j. znaci da je na prvoj koci pao broj i a na kocki 2 broj j.
 moze poprimiti vrijednost -5 samo ako je moze poprimiti vrijednost -5 samo ako je 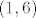 , vrijednost -4 samo ako je , vrijednost -4 samo ako je 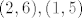 , vrijednost -3 samo ako je , vrijednost -3 samo ako je 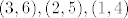 , vrijednost -2 samo ako je , vrijednost -2 samo ako je 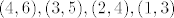 , vrijednost -1 samo ako je , vrijednost -1 samo ako je 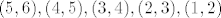 , te vrijednost 0 samo ako je , te vrijednost 0 samo ako je 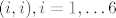 . Vrijednosti 1,...,5 idu po analogiji, samo vrijednost . Vrijednosti 1,...,5 idu po analogiji, samo vrijednost 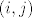 zamijenis sa zamijenis sa 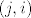 . Sada jos samo treba naci vjerojatnost . Sada jos samo treba naci vjerojatnost 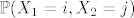 , no buduci da se kocke bacaju nezavisno ( inace ovo nista ne ide ), ta vjerojatnost je ocigledno 1/36. Napisimo sada razdiobu od X_1-X_2 , no buduci da se kocke bacaju nezavisno ( inace ovo nista ne ide ), ta vjerojatnost je ocigledno 1/36. Napisimo sada razdiobu od X_1-X_2
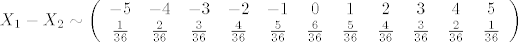 . .
Zadatak necu zavrsiti jer cevape nisam dobio!!!!
|
|
| [Vrh] |
|
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
|
| [Vrh] |
|
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
 Postano: 12:19 ned, 11. 1. 2009 Naslov: Postano: 12:19 ned, 11. 1. 2009 Naslov: |
    |
|
|
ispala mi je razdioba 0,1,2,3,4,5
A vjerovatnosti formulom P(Xi)=(5 povrh i) * (1/6)^2 ; i=0....5
Jel dobro?
Ne štima ova formula za vjerovatnost jel da...hmm
ispala mi je razdioba 0,1,2,3,4,5
A vjerovatnosti formulom P(Xi)=(5 povrh i) * (1/6)^2 ; i=0....5
Jel dobro?
Ne štima ova formula za vjerovatnost jel da...hmm
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 14:55 ned, 11. 1. 2009 Naslov: Postano: 14:55 ned, 11. 1. 2009 Naslov: |
    |
|
|
[quote="baky0905"]ispala mi je razdioba 0,1,2,3,4,5
A vjerovatnosti formulom P(Xi)=(5 povrh i) * (1/6)^2 ; i=0....5
Jel dobro?
Ne štima ova formula za vjerovatnost jel da...hmm[/quote]
Da, ne štima ovo za vjerojatnosti jer suma vjerojatnosti mora bit 1.
Ja bi reko da | X1-X2| može poprimit 0,1,2,3,4,5 i sad samo pozbrajaj kaj dolje piše... otprilike bi trebalo bit:
[latex]| X_1-X_2| \sim \left(\begin{array}{ccccccccccc}
0 & 1 & 2 & 3 & 4 & 5 \\
\frac{6}{36} & \frac{10}{36} & \frac{8}{36} & \frac{6}{36} & \frac{4}{36} & \frac{2}{36} \\
\end{array}\right) [/latex]
| baky0905 (napisa): | ispala mi je razdioba 0,1,2,3,4,5
A vjerovatnosti formulom P(Xi)=(5 povrh i) * (1/6)^2 ; i=0....5
Jel dobro?
Ne štima ova formula za vjerovatnost jel da...hmm |
Da, ne štima ovo za vjerojatnosti jer suma vjerojatnosti mora bit 1.
Ja bi reko da | X1-X2| može poprimit 0,1,2,3,4,5 i sad samo pozbrajaj kaj dolje piše... otprilike bi trebalo bit:
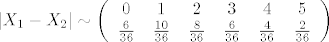
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
|
| [Vrh] |
|
Atomised
Forumaš(ica)


Pridružen/a: 04. 09. 2007. (15:33:59)
Postovi: (399)16
Lokacija: Exotica
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 16:06 pon, 12. 1. 2009 Naslov: Postano: 16:06 pon, 12. 1. 2009 Naslov: |
    |
|
|
[quote="baky0905"]znam da mora biti jedan, a kak si došao do tih vjerojatnosti?
Hvala![/quote]
Kako je Atomised rekao :D
A inače, prebrojiš slučajeve...
recimo slučaj kad je |X1-X2|=4. Tu su slučajevi:
(1,5), (5,1), (6,2), (2,6). Njih je 4, svaki je vjerojatan sa vjerojatnošću 1/36 -> P (|X1-X2|=4) = 4/36.
8)
| baky0905 (napisa): | znam da mora biti jedan, a kak si došao do tih vjerojatnosti?
Hvala! |
Kako je Atomised rekao 
A inače, prebrojiš slučajeve...
recimo slučaj kad je |X1-X2|=4. Tu su slučajevi:
(1,5), (5,1), (6,2), (2,6). Njih je 4, svaki je vjerojatan sa vjerojatnošću 1/36 → P (|X1-X2|=4) = 4/36.

_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
 Postano: 20:39 pon, 12. 1. 2009 Naslov: Postano: 20:39 pon, 12. 1. 2009 Naslov: |
    |
|
|
Može još ako vam se da ovo:
1.Šiffra se sastoji od 3 brojke izabrane između 0,1,2,3,4,5,6,7,8,9.
a)Koliko je različitih šifri moguće sastaviti? dobio sam 1000
b)koliko od tih šifri ima 3 različita broja? izračunao sam 720
c)Kolika je vjerovatnost da nasumce izabrana šifra ima 2 ili 3 broja međusobno jednaka? to ne znam:) molim pomoć
d) ako je izabrana šifra s 3 različite brojke, kolika je vjerovatnost da je jedna od tih brojki brojka 9? izračunao sam 3/10
Možete samo provjerit jel sam ovo dobro rješio:
2.
Oznaka na knjizi sastoji se od bilo koje neparne tri brojke i 2 različita samoglasnika.
a)Koliko se knjiga može na taj način označiti različitim oznakama? dobio sam 125*20* 5 povrh 2 = 25 000
b)Koliko od tih knjiga u toj oznaci ima 3 različita broja?
5*4*3*5*4* 5 povrh 2= 12 000
c)Kolika je vjerovatnost da nasumce izabrana knjiga u oznaci ima 2 ili sva 3 broja jednaka? ne znam ,molim pomoc
d)Ako je izabrana knjiga sa 3 različita broja kolika je vjerovatnost da sadrži slovo a? dobio sam 2/5
hvala
Može još ako vam se da ovo:
1.Šiffra se sastoji od 3 brojke izabrane između 0,1,2,3,4,5,6,7,8,9.
a)Koliko je različitih šifri moguće sastaviti? dobio sam 1000
b)koliko od tih šifri ima 3 različita broja? izračunao sam 720
c)Kolika je vjerovatnost da nasumce izabrana šifra ima 2 ili 3 broja međusobno jednaka? to ne znam:) molim pomoć
d) ako je izabrana šifra s 3 različite brojke, kolika je vjerovatnost da je jedna od tih brojki brojka 9? izračunao sam 3/10
Možete samo provjerit jel sam ovo dobro rješio:
2.
Oznaka na knjizi sastoji se od bilo koje neparne tri brojke i 2 različita samoglasnika.
a)Koliko se knjiga može na taj način označiti različitim oznakama? dobio sam 125*20* 5 povrh 2 = 25 000
b)Koliko od tih knjiga u toj oznaci ima 3 različita broja?
5*4*3*5*4* 5 povrh 2= 12 000
c)Kolika je vjerovatnost da nasumce izabrana knjiga u oznaci ima 2 ili sva 3 broja jednaka? ne znam ,molim pomoc
d)Ako je izabrana knjiga sa 3 različita broja kolika je vjerovatnost da sadrži slovo a? dobio sam 2/5
hvala
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 21:50 pon, 12. 1. 2009 Naslov: Postano: 21:50 pon, 12. 1. 2009 Naslov: |
    |
|
|
[quote="baky0905"]Može još ako vam se da ovo:
1.Šiffra se sastoji od 3 brojke izabrane između 0,1,2,3,4,5,6,7,8,9.
a)Koliko je različitih šifri moguće sastaviti? dobio sam 1000
b)koliko od tih šifri ima 3 različita broja? izračunao sam 720
c)Kolika je vjerovatnost da nasumce izabrana šifra ima 2 ili 3 broja međusobno jednaka? to ne znam:) molim pomoć
d) ako je izabrana šifra s 3 različite brojke, kolika je vjerovatnost da je jedna od tih brojki brojka 9? izračunao sam 3/10
Možete samo provjerit jel sam ovo dobro rješio:
2.
Oznaka na knjizi sastoji se od bilo koje neparne tri brojke i 2 različita samoglasnika.
a)Koliko se knjiga može na taj način označiti različitim oznakama? dobio sam 125*20* 5 povrh 2 = 25 000
b)Koliko od tih knjiga u toj oznaci ima 3 različita broja?
5*4*3*5*4* 5 povrh 2= 12 000
c)Kolika je vjerovatnost da nasumce izabrana knjiga u oznaci ima 2 ili sva 3 broja jednaka? ne znam ,molim pomoc
d)Ako je izabrana knjiga sa 3 različita broja kolika je vjerovatnost da sadrži slovo a? dobio sam 2/5
hvala[/quote]
1.
a) 10*10*10 = 1000 ;)
b) 10*9*8=720 ;)
c) ovako... tu ide malo kombinatorike... tražena vjer je broj_povoljnih_šifri/sve šifre.
povoljne šifre su one koje imaju 3 broja ista ili 2 broja ista. (primjeti ili)
2 broja: biramo taj broj na (10 povrh 1) načina i još jedan broj izaberemo na 9 načina (jer ne smijemo onaj koji smoo uzeli da bude dupli). I sad je ukupan broj načina (10 povrh 1)*9*3!/2! (ove faktorijele jer gledamo broj permutacija s ponavljanjem skupa od 3 elementa, i imamo ponavljanja (permutacije multiskupa)).
Ovo nam je prebrojalo sve šifre oblika aab,aba,baa.
kad su sve brojke iste onda je broj povoljnih 10.
Ukupno: 10+(10 povrh 1)*9*3!/2! = 280.
pa je tražena vjerojatnost 280/1000.
(primjeti, ovo su nam svi slučaji različiti od onog u b) )
d) tražena vjer je : 3*9*8/720 = 3/10 ;)
2. slično. Samo pazi kad prebrojavaš slučajeve :D
| baky0905 (napisa): | Može još ako vam se da ovo:
1.Šiffra se sastoji od 3 brojke izabrane između 0,1,2,3,4,5,6,7,8,9.
a)Koliko je različitih šifri moguće sastaviti? dobio sam 1000
b)koliko od tih šifri ima 3 različita broja? izračunao sam 720
c)Kolika je vjerovatnost da nasumce izabrana šifra ima 2 ili 3 broja međusobno jednaka? to ne znam:) molim pomoć
d) ako je izabrana šifra s 3 različite brojke, kolika je vjerovatnost da je jedna od tih brojki brojka 9? izračunao sam 3/10
Možete samo provjerit jel sam ovo dobro rješio:
2.
Oznaka na knjizi sastoji se od bilo koje neparne tri brojke i 2 različita samoglasnika.
a)Koliko se knjiga može na taj način označiti različitim oznakama? dobio sam 125*20* 5 povrh 2 = 25 000
b)Koliko od tih knjiga u toj oznaci ima 3 različita broja?
5*4*3*5*4* 5 povrh 2= 12 000
c)Kolika je vjerovatnost da nasumce izabrana knjiga u oznaci ima 2 ili sva 3 broja jednaka? ne znam ,molim pomoc
d)Ako je izabrana knjiga sa 3 različita broja kolika je vjerovatnost da sadrži slovo a? dobio sam 2/5
hvala |
1.
a) 10*10*10 = 1000 
b) 10*9*8=720 
c) ovako... tu ide malo kombinatorike... tražena vjer je broj_povoljnih_šifri/sve šifre.
povoljne šifre su one koje imaju 3 broja ista ili 2 broja ista. (primjeti ili)
2 broja: biramo taj broj na (10 povrh 1) načina i još jedan broj izaberemo na 9 načina (jer ne smijemo onaj koji smoo uzeli da bude dupli). I sad je ukupan broj načina (10 povrh 1)*9*3!/2! (ove faktorijele jer gledamo broj permutacija s ponavljanjem skupa od 3 elementa, i imamo ponavljanja (permutacije multiskupa)).
Ovo nam je prebrojalo sve šifre oblika aab,aba,baa.
kad su sve brojke iste onda je broj povoljnih 10.
Ukupno: 10+(10 povrh 1)*9*3!/2! = 280.
pa je tražena vjerojatnost 280/1000.
(primjeti, ovo su nam svi slučaji različiti od onog u b) )
d) tražena vjer je : 3*9*8/720 = 3/10 
2. slično. Samo pazi kad prebrojavaš slučajeve 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
baky0905
Forumaš(ica)

Pridružen/a: 05. 01. 2009. (17:54:24)
Postovi: (1B)16
|
|
| [Vrh] |
|
|







