| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
 Postano: 8:10 ned, 18. 1. 2009 Naslov: Nekoliko pitanja o 7. zadaci Postano: 8:10 ned, 18. 1. 2009 Naslov: Nekoliko pitanja o 7. zadaci |
    |
|
|
u 3. zadatku,
[quote]Odredite broj multigrafova koji imaju [latex]n[/latex] vrhova i [latex]m[/latex] bridova.[/quote]
ubrajamo li i medjusobno izomorfne grafove? jer onda, ako ima [latex]n[/latex] vrhova, proizvoljan brid biramo na [latex]\binom{n}{2}[/latex] nacina, pa [latex]m[/latex] bridova biramo na [latex]\binom{n}{2}^m[/latex] nacina. ili je odgovor nesto drugo?
u 4. zadatku,
[quote]Odredite broj medjusobno neizomorfnih jednostavnih grafova s 5 vrhova.[/quote]
da li se ocekuje da kao na vjezbama sve grafove nacrtamo pa prebrojimo, znaci klase grafova sa 0, 1, 2,..,10 bridova ili postoji neki racunski postupak (jer se trazi samo broj takvih grafova)?
u 1. zadatku pod a),
[quote]Koliko ima grafova s 5 vrhova stupnja 1,1,2,2,2[/quote]
krenuo sam crtati par takvih grafova ali mi se cini da bi do broja takvih grafova trebalo doci racunski, uostalom u jednom proslogodisnjem topicu pise:
[quote="mmaric43"]Mene konkretno iz 8. zadaće prvi zadatak da matematički riješim (ili kako već) koliko ima grafova koji imaju 5 vrhova stupnjeva 1,1,2,2,2 ( [b]ne možeš crtajući pokazivati[/b]) a prije mene je pitala nešto tipa četvrtog na kolokviju. [/quote]
pa ako bi mi netko imao hint ili uputu kako to napraviti bio bih jako zahvalan.
unaprijed hvala na pomoci :)
u 3. zadatku,
| Citat: | Odredite broj multigrafova koji imaju  vrhova i vrhova i  bridova. bridova. |
ubrajamo li i medjusobno izomorfne grafove? jer onda, ako ima  vrhova, proizvoljan brid biramo na vrhova, proizvoljan brid biramo na 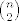 nacina, pa nacina, pa  bridova biramo na bridova biramo na 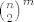 nacina. ili je odgovor nesto drugo? nacina. ili je odgovor nesto drugo?
u 4. zadatku,
| Citat: | | Odredite broj medjusobno neizomorfnih jednostavnih grafova s 5 vrhova. |
da li se ocekuje da kao na vjezbama sve grafove nacrtamo pa prebrojimo, znaci klase grafova sa 0, 1, 2,..,10 bridova ili postoji neki racunski postupak (jer se trazi samo broj takvih grafova)?
u 1. zadatku pod a),
| Citat: | | Koliko ima grafova s 5 vrhova stupnja 1,1,2,2,2 |
krenuo sam crtati par takvih grafova ali mi se cini da bi do broja takvih grafova trebalo doci racunski, uostalom u jednom proslogodisnjem topicu pise:
| mmaric43 (napisa): | | Mene konkretno iz 8. zadaće prvi zadatak da matematički riješim (ili kako već) koliko ima grafova koji imaju 5 vrhova stupnjeva 1,1,2,2,2 ( ne možeš crtajući pokazivati) a prije mene je pitala nešto tipa četvrtog na kolokviju. |
pa ako bi mi netko imao hint ili uputu kako to napraviti bio bih jako zahvalan.
unaprijed hvala na pomoci 
_________________  |
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
gaston
Forumaš(ica)


Pridružen/a: 10. 07. 2008. (15:42:28)
Postovi: (21)16
|
 Postano: 18:18 ned, 18. 1. 2009 Naslov: Postano: 18:18 ned, 18. 1. 2009 Naslov: |
    |
|
|
[quote="Novi"]Jel 8 treba ovako glasit? Nema previse smisla. Tvrdnja govori o grafovima sa p vrhova gdje svi vrhovi imaju stupanj veći ili jednak p(p-1)/2. Ali općenito neki vrh u grafu sa p vrhova (naravno jednostavnom) nemože imati stupanj veći od p-1, pa ova tvrdnja nema previše smisla. Mozda samo u slucaju p=1 ili 2.[/quote]
cini mi se da bi trebalo biti [latex]\frac{p-1}{2}[/latex].
jer onda je zadatak: imamo jednostavan graf sa p vrhova, gdje svaki vrh ima stupanj [latex]\frac{p-1}{2}[/latex].
e sad, ako imamo jednu komponentu povezanosti, u njoj mora biti barem, odnosno vise ili jednako od [latex]1+\frac{p-1}{2}[/latex] vrhova, sto je strogo vece od [latex]\frac{p}{2}[/latex] vrhova. ali ne mozes imati dvije komponente povezanosti u kojoj svaka ima strogo vise od [latex]\frac{p}{2}[/latex] vrhova, pa slijedi da u takvom grafu moze biti samo jedna komponenta povezanosti, odnosno da je graf povezan. :)
je li netko rijesio 6. d)?
jesu li sljedeci grafovi izomorfni:
[img]http://i43.tinypic.com/2gyazx0.jpg[/img]
od kud krenuti, kako poceti? svi vrhovi su stupnja 3, pa ne mozemo odabrati skupove od 3-4 vrha istog stupnja u oba grafa i gledati inducirane podgrafove... :?
| Novi (napisa): | | Jel 8 treba ovako glasit? Nema previse smisla. Tvrdnja govori o grafovima sa p vrhova gdje svi vrhovi imaju stupanj veći ili jednak p(p-1)/2. Ali općenito neki vrh u grafu sa p vrhova (naravno jednostavnom) nemože imati stupanj veći od p-1, pa ova tvrdnja nema previše smisla. Mozda samo u slucaju p=1 ili 2. |
cini mi se da bi trebalo biti 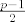 . .
jer onda je zadatak: imamo jednostavan graf sa p vrhova, gdje svaki vrh ima stupanj 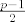 . .
e sad, ako imamo jednu komponentu povezanosti, u njoj mora biti barem, odnosno vise ili jednako od 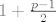 vrhova, sto je strogo vece od vrhova, sto je strogo vece od 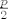 vrhova. ali ne mozes imati dvije komponente povezanosti u kojoj svaka ima strogo vise od vrhova. ali ne mozes imati dvije komponente povezanosti u kojoj svaka ima strogo vise od 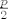 vrhova, pa slijedi da u takvom grafu moze biti samo jedna komponenta povezanosti, odnosno da je graf povezan. vrhova, pa slijedi da u takvom grafu moze biti samo jedna komponenta povezanosti, odnosno da je graf povezan. 
je li netko rijesio 6. d)?
jesu li sljedeci grafovi izomorfni:

od kud krenuti, kako poceti? svi vrhovi su stupnja 3, pa ne mozemo odabrati skupove od 3-4 vrha istog stupnja u oba grafa i gledati inducirane podgrafove... 
_________________  |
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
 Postano: 1:11 sri, 21. 1. 2009 Naslov: Postano: 1:11 sri, 21. 1. 2009 Naslov: |
    |
|
|
[size=12]jel kuži netko zadatak s vježbi u kojem se traži broj razapinjućih stabala grafa K 2,m?
zašto smo napisali "u particuji B bit će jedan vrh stupnja 2 i m-1 vrhova stupnja 1"? otkud to?
i što točno znači K 2,m? znam da je K n = potpuni graf s n vrhova, al ovo...
[/size]
[size=9]da ne bi bili zabune, ovo nie offtopic jer je u zadaći isti zadatak samo za K 3, m[/size] :wink:
jel kuži netko zadatak s vježbi u kojem se traži broj razapinjućih stabala grafa K 2,m?
zašto smo napisali "u particuji B bit će jedan vrh stupnja 2 i m-1 vrhova stupnja 1"? otkud to?
i što točno znači K 2,m? znam da je K n = potpuni graf s n vrhova, al ovo...
da ne bi bili zabune, ovo nie offtopic jer je u zadaći isti zadatak samo za K 3, m 
|
|
| [Vrh] |
|
MB
Forumaš(ica)


Pridružen/a: 01. 07. 2005. (12:35:21)
Postovi: (224)16
Spol: 
Lokacija: Molvice
|
 Postano: 11:00 sri, 21. 1. 2009 Naslov: Postano: 11:00 sri, 21. 1. 2009 Naslov: |
    |
|
|
[latex]$K_{n,m}$[/latex] je oznaka za potpun BIPARTITAN GRAF u kojem particije imaju [latex]$n$[/latex] odnosno [latex]$m$[/latex] vrhova. Bipartitan graf je onaj u kojem vrhove mozemo particionirati na 2 dijela A i B (A, B neprazni, A unija B= V), tako da su svi bridovi oblika {a,b} za a iz A i b iz B (dakle, vrhovi iz A nikad nisu međusobno spojeni i slično za B).
Za [latex]$K_{2,m}$[/latex]:
U B svaki vrh mora biti barem stupnja 1 jer je razapinjajuce stablo podgraf na svim vrhovima pocetnog grafa, jedan od tih vrhova mora biti stupnja barem 2 jer bismo inace imali 2 komponente povazanosti. Stupnjevi ne mogu biti veci jer bismo tada zatvorili neki ciklus (tj. podgraf bi imao vise od n-1 brida, pa ne bi bio stablo).
Brojimo neizomorfna razapinjajuca stabla, razlikujemo izomorfna stabla po oznakama vrhova.
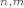 je oznaka za potpun BIPARTITAN GRAF u kojem particije imaju je oznaka za potpun BIPARTITAN GRAF u kojem particije imaju  odnosno odnosno  vrhova. Bipartitan graf je onaj u kojem vrhove mozemo particionirati na 2 dijela A i B (A, B neprazni, A unija B= V), tako da su svi bridovi oblika {a,b} za a iz A i b iz B (dakle, vrhovi iz A nikad nisu međusobno spojeni i slično za B). vrhova. Bipartitan graf je onaj u kojem vrhove mozemo particionirati na 2 dijela A i B (A, B neprazni, A unija B= V), tako da su svi bridovi oblika {a,b} za a iz A i b iz B (dakle, vrhovi iz A nikad nisu međusobno spojeni i slično za B).
Za 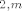 : :
U B svaki vrh mora biti barem stupnja 1 jer je razapinjajuce stablo podgraf na svim vrhovima pocetnog grafa, jedan od tih vrhova mora biti stupnja barem 2 jer bismo inace imali 2 komponente povazanosti. Stupnjevi ne mogu biti veci jer bismo tada zatvorili neki ciklus (tj. podgraf bi imao vise od n-1 brida, pa ne bi bio stablo).
Brojimo neizomorfna razapinjajuca stabla, razlikujemo izomorfna stabla po oznakama vrhova.
_________________  |
|
| [Vrh] |
|
lucika
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (17:52:27)
Postovi: (12F)16
Spol: 
|
|
| [Vrh] |
|
|










