|
Može :)
evo ga 7. i 14.
[b]7.[/b] označimo
[latex]A_{m,n} = \frac{12m + n - 3mn +7}{5m - 2n - 2mn + 5} = \frac{\left(5m-2mn\right)+\left(7m+7\right)-\left(n+mn\right) + \left(2n-5\right) + 5}{\left(m+1\right)\left(5-2n\right)}=[/latex]
[latex]=\frac{\left(m-1\right)\left(5-2n\right) + \left(7-n\right)\left(m+1\right) + 5}{\left(m+1\right)\left(5-2n\right)} = \frac{3}{2} - \frac{2}{m+1} + \frac{5}{\left(m+1\right)\left(5-2n\right)} + \frac{9}{10-4n}[/latex].
Dalje, uvodimo sljedeću oznaku, za [latex]n \in \mathbb{N}[/latex] (fiksni), neka je [latex]S_n=\left\{A_{m,n} \colon m \in \mathbb{N}\right\}[/latex]. Dalje, očito je da postoje i [latex]\inf{S}[/latex] i [latex]\sup{S}[/latex], tada vidimo da je
[latex]\inf{S}=\min{\left\{\inf{S_n} \colon n \in \mathbb{N}\right\}}[/latex] i [latex]\sup{S}=\max{\left\{\sup{S_n} \colon n \in \mathbb{N}\right\}}[/latex].
Promotrimo tri slučaja:
[b]1°[/b] [latex]n=1[/latex], vrijedi [latex]A_{m,1}=3-\frac{1}{3\left(m+1\right)}[/latex], odmah vidimo da je [latex]\inf{S_1}=\frac{17}{6}[/latex], za [latex]m=1[/latex], a [latex]\sup{S_1}=3[/latex], kada [latex]m \to +\infty[/latex].
[b]2°[/b] [latex]n=2[/latex], vrijedi [latex]A_{m,2}=6+\frac{3}{m+1}[/latex], odmah vidimo da je [latex]\inf{S_2}=6[/latex], kada [latex]m \to +\infty[/latex], te [latex]\sup{S_2}=\frac{15}{2}[/latex], za [latex]m=1[/latex].
[b]3°[/b] [latex]n \geq 3[/latex], tada je [latex]A_{m,n}=\frac{3}{2}-\left(\underbrace{\frac{2}{m+1}+\frac{5}{\left(m+1\right)\left(2n-1\right)}+\frac{9}{4n-10}}_{B_{m,n}}\right)[/latex], očito je [latex]B_{m,n}>0[/latex], [latex]\forall n \in \mathbb{N} \setminus \left\{1,2\right\}[/latex], stoga je [latex]A_{m,n}<\frac{3}{2}[/latex], [latex]\forall m,n \in \mathbb{N}, n \geq 3[/latex]. Zbog svega ovoga je očito da je [latex]\sup{S_n} \leq \frac{3}{2}[/latex], [latex]\forall n \in \mathbb{N} \setminus \left\{1,2\right\}[/latex].
Sada lako zaključujemo da je [b][latex]\sup{S}=\frac{15}{2}[/latex][/b], te da se postiže za [latex]m=1[/latex] i [latex]n=2[/latex].
Dalje, očito vrijede sljedeće nejednakosti (uz [latex]m,n \in \mathbb{N}, n \geq 3[/latex])
[latex]\frac{2}{m+1} \leq \frac{2}{1+1} = 3[/latex], [latex]\frac{5}{\left(m+1\right)\left(2n-5\right)} \leq \frac{5}{\left(1+1\right)\left(6-5\right)}=\frac{5}{2}[/latex], [latex]\frac{9}{4n-10} \leq \frac{9}{12-10} = \frac{9}{2}[/latex]. Zato je [latex]B_{m,n} \leq 8[/latex], a zbog svega toga [latex]A_{m,n} \geq \frac{3}{2} - 8 = \frac{-13}{2}[/latex], [latex]\forall m,n \in \mathbb{N}, n\geq 3[/latex].
Konačno zaključujemo da je [latex]\inf{S}=\frac{-13}{2}[/latex], te da se postiže za [latex]m=1[/latex] i [latex]n=3[/latex].
[b]14.[/b] Očito je ispunjena nejednakost
[latex]\frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+a} > \frac{a}{a+b+c} + \frac{b}{b+c+a} + \frac{c}{c+a+b} = 1[/latex], sada je još dovoljno pokazati da se dani izraz može po volji približiti jedinici i time smo pokazali da je [latex]\inf{S}=1[/latex]. To lako vidimo da se dešava za [latex]a \to 0[/latex], [latex]b=1[/latex] i [latex]c \to + \infty[/latex], tada
[latex]\frac{a}{a+b} = \frac{a}{a+1} \to 0[/latex], [latex]\frac{b}{b+c}=\frac{1}{1+c} \to 0[/latex], [latex]\frac{c}{c+a}=\frac{1}{1+\frac{a}{c}} \to 1[/latex]. Dakle, [latex]\frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+a} \to 0 + 0 + 1 = 1[/latex].
Također, očito vrijedi [latex]\frac{b}{a+b} + \frac{c}{b+c} + \frac{a}{c+a} > \frac{b}{a+b+c} + \frac{c}{b+c+a} + \frac{a}{c+a+b} = 1[/latex], a kako je [latex]\left(\frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+a}\right) + \left(\frac{b}{a+b} + \frac{c}{b+c} + \frac{a}{c+a}\right)=3[/latex], vidimo da vrijedi da je [latex]\frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+a} < 2[/latex].
Sada je dovoljno pokazati da se dani izraz može po volji približiti dvojci i dokazali smo da je [latex]\sup{S}=2[/latex].
Zaista, stavimo li [latex]a=1[/latex], [latex]b \to 0[/latex] i [latex]c \to +\infty[/latex] imamo [latex]\frac{a}{a+b}=\frac{1}{1+b} \to 1[/latex], [latex]\frac{b}{b+c} \to 0[/latex], [latex]\frac{c}{c+a} = \frac{1}{1+\frac{1}{c}} \to 1[/latex]. Dakle, [latex]\frac{a}{a+b} + \frac{b}{b+c} + \frac{c}{c+a} \to 1 + 0 + 1 = 2[/latex].
Može 
evo ga 7. i 14.
7. označimo
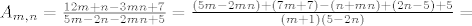
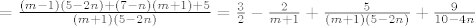 . .
Dalje, uvodimo sljedeću oznaku, za  (fiksni), neka je (fiksni), neka je 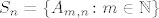 . Dalje, očito je da postoje i . Dalje, očito je da postoje i 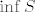 i i 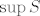 , tada vidimo da je , tada vidimo da je
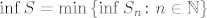 i i 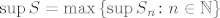 . .
Promotrimo tri slučaja:
1° 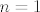 , vrijedi , vrijedi 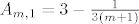 , odmah vidimo da je , odmah vidimo da je 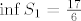 , za , za 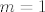 , a , a 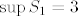 , kada , kada 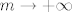 . .
2°  , vrijedi , vrijedi 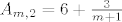 , odmah vidimo da je , odmah vidimo da je 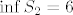 , kada , kada 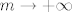 , te , te 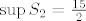 , za , za 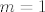 . .
3° 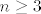 , tada je , tada je 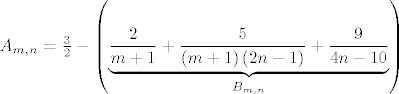 , očito je , očito je 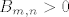 , , 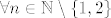 , stoga je , stoga je 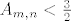 , , 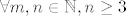 . Zbog svega ovoga je očito da je . Zbog svega ovoga je očito da je 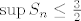 , , 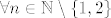 . .
Sada lako zaključujemo da je 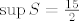 , te da se postiže za , te da se postiže za 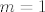 i i  . .
Dalje, očito vrijede sljedeće nejednakosti (uz 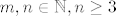 ) )
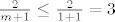 , , 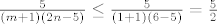 , , 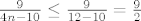 . Zato je . Zato je 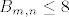 , a zbog svega toga , a zbog svega toga 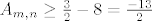 , , 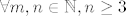 . .
Konačno zaključujemo da je 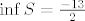 , te da se postiže za , te da se postiže za 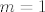 i i 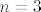 . .
14. Očito je ispunjena nejednakost
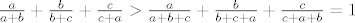 , sada je još dovoljno pokazati da se dani izraz može po volji približiti jedinici i time smo pokazali da je , sada je još dovoljno pokazati da se dani izraz može po volji približiti jedinici i time smo pokazali da je 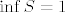 . To lako vidimo da se dešava za . To lako vidimo da se dešava za 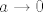 , , 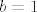 i i 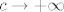 , tada , tada
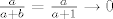 , , 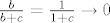 , , 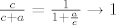 . Dakle, . Dakle, 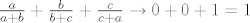 . .
Također, očito vrijedi 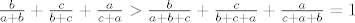 , a kako je , a kako je 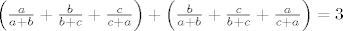 , vidimo da vrijedi da je , vidimo da vrijedi da je 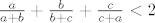 . .
Sada je dovoljno pokazati da se dani izraz može po volji približiti dvojci i dokazali smo da je 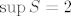 . .
Zaista, stavimo li 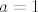 , , 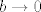 i i 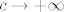 imamo imamo 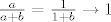 , , 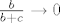 , , 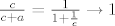 . Dakle, . Dakle, 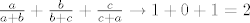 . .
|









