| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
 Postano: 17:29 sri, 28. 1. 2009 Naslov: 5. Domaća zadaća Postano: 17:29 sri, 28. 1. 2009 Naslov: 5. Domaća zadaća |
    |
|
|
7. zadatak
Nađite sve a,b iz R tako da polinom p(x)=x^4 - 4x^3 + 10x^2 + ax + b ima dvije dvostruke nultocke...
Ugl, napisao sam da je p(x)=(x-x1)^2*(x-x2)^2. Onda sam to izmnozio i izjednacio i dobio sustav
x1+x2=2
x1*x2=3
ugl, x1 i x2 su kompleksni i nakon jos malo igranja ispalo mi je a=-12 b=2...
jel to tocno, a ak nije jel moze neko napisati tocno rjesenje....
unaprijed hvala...
7. zadatak
Nađite sve a,b iz R tako da polinom p(x)=x^4 - 4x^3 + 10x^2 + ax + b ima dvije dvostruke nultocke...
Ugl, napisao sam da je p(x)=(x-x1)^2*(x-x2)^2. Onda sam to izmnozio i izjednacio i dobio sustav
x1+x2=2
x1*x2=3
ugl, x1 i x2 su kompleksni i nakon jos malo igranja ispalo mi je a=-12 b=2...
jel to tocno, a ak nije jel moze neko napisati tocno rjesenje....
unaprijed hvala...
Zadnja promjena: tomitza; 20:18 sri, 28. 1. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 23:19 sri, 28. 1. 2009 Naslov: Postano: 23:19 sri, 28. 1. 2009 Naslov: |
    |
|
|
[quote="tomitza"]i btw... kak si ti to rijesio... :)[/quote]
pa dakle...
neka su [latex]c[/latex] i [latex]d[/latex] nultocke
iz vietovih:
[latex]c\cdot c\cdot d\cdot d=b[/latex]
[latex]c+c+d+d=4[/latex]
dakle
[latex]c^2d^2=b[/latex] [latex](1)[/latex]
[latex]c+d=2[/latex]
deriviranjem dobijemo polinom treceg stupnja
on ima dakle tri nultocke, ali jedna je [latex]c[/latex], jedna je [latex]d[/latex], treca neka je [latex]e[/latex], opet vietove:
[latex]c\cdot d\cdot e=\frac{a}{4}[/latex] [latex](2)[/latex]
[latex]c+d+e=3\Rightarrow e=1[/latex] jer mi je [latex]c+d=2[/latex]
sad djelim derivirani [latex]p[/latex] sa [latex]x-1[/latex], dobim ostatak [latex]a+12[/latex], ali to je [latex]0[/latex], dakle [latex]a=-12[/latex]
uvrstavanjem [latex]e[/latex] u [latex](2)[/latex] te kvadriranjem i uvrstavanjem u [latex](1)[/latex] dobimo [latex]b[/latex]
| tomitza (napisa): | i btw... kak si ti to rijesio...  |
pa dakle...
neka su  i i 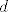 nultocke nultocke
iz vietovih:
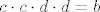
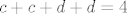
dakle
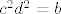 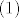
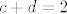
deriviranjem dobijemo polinom treceg stupnja
on ima dakle tri nultocke, ali jedna je  , jedna je , jedna je 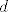 , treca neka je , treca neka je  , opet vietove: , opet vietove:
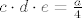 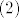
 jer mi je jer mi je 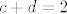
sad djelim derivirani  sa sa 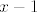 , dobim ostatak , dobim ostatak  , ali to je , ali to je  , dakle , dakle 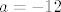
uvrstavanjem  u u 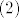 te kvadriranjem i uvrstavanjem u te kvadriranjem i uvrstavanjem u 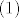 dobimo dobimo 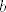
_________________
Mario Berljafa
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
 Postano: 19:26 uto, 3. 2. 2009 Naslov: Postano: 19:26 uto, 3. 2. 2009 Naslov: |
    |
|
|
Hvala!!
i još jedno pitanje:
u 5.zadatku sam dobila 2 rješenja: a=-12 i b=16
a=-3 i b=-2
i kada se uvrsti, ispada da je x=-1 nultocka za p(x) i njegove prve derivacije, to je za a=-3 i b=-2, a za a=-12 i b=16 nultocka oba polinoma je 2.
i sad,ima li 2 rješenja(ali to onda znaci da ima 2 dvostruke nultocke) ili sam ja nešto krivo rješila? :?
Hvala!!
i još jedno pitanje:
u 5.zadatku sam dobila 2 rješenja: a=-12 i b=16
a=-3 i b=-2
i kada se uvrsti, ispada da je x=-1 nultocka za p(x) i njegove prve derivacije, to je za a=-3 i b=-2, a za a=-12 i b=16 nultocka oba polinoma je 2.
i sad,ima li 2 rješenja(ali to onda znaci da ima 2 dvostruke nultocke) ili sam ja nešto krivo rješila? 
_________________
u raju je lijepo,ali u paklu je ekipa
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
uzorni student
Forumaš(ica)

Pridružen/a: 24. 01. 2009. (16:11:39)
Postovi: (2C)16
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 10:29 sri, 4. 2. 2009 Naslov: Postano: 10:29 sri, 4. 2. 2009 Naslov: |
    |
|
|
prvi zadatak.
imaš da je f=g*q+r. znaš q, i znaš r. zanima te kolko je f/q. sad podjeliš sve skupa sa q. dobiš: f/q=g+r/q. i sad podjeli ovaj r sa q. dobije se nešto plus ostatak. taj ostatak je neki r_1/q, tak ga zapišeš. i sad opet pomnoži sve skupa cijelu jednakost sa q. dobije se f=(g+"nešto što se dobilo djeljenjem r-a sa q")*q+r_1. i sad je taj polinom f zapisan u obliku f=g_1*q+r_1. g_1=g+"nešto što se dobilo djeljenjem r-a sa q". traženi ostatak je ovaj r_1.
u biti, treba podjelit r sa q i njihov ostatak je ostatak koji daje f kad se dijeli sa q.
prvi zadatak.
imaš da je f=g*q+r. znaš q, i znaš r. zanima te kolko je f/q. sad podjeliš sve skupa sa q. dobiš: f/q=g+r/q. i sad podjeli ovaj r sa q. dobije se nešto plus ostatak. taj ostatak je neki r_1/q, tak ga zapišeš. i sad opet pomnoži sve skupa cijelu jednakost sa q. dobije se f=(g+"nešto što se dobilo djeljenjem r-a sa q")*q+r_1. i sad je taj polinom f zapisan u obliku f=g_1*q+r_1. g_1=g+"nešto što se dobilo djeljenjem r-a sa q". traženi ostatak je ovaj r_1.
u biti, treba podjelit r sa q i njihov ostatak je ostatak koji daje f kad se dijeli sa q.
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 11:20 sri, 4. 2. 2009 Naslov: Postano: 11:20 sri, 4. 2. 2009 Naslov: |
    |
|
|
@mycky1111
[latex]4.\textrm{ M}\left( f,g,h\right)=1[/latex]
@bad_angel
sorry
neznam kako sam to rjesavao, al dosta je lako sa vietovim formulama, odmah dobis da je [latex]x_2=x_3=-1[/latex], jer je [latex]x_1+x_2+x_3=0[/latex], odredit [latex]a[/latex] i [latex]b[/latex] je sad trivijalno
@mycky1111
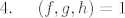
@bad_angel
sorry
neznam kako sam to rjesavao, al dosta je lako sa vietovim formulama, odmah dobis da je 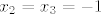 , jer je , jer je 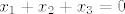 , odredit , odredit  i i 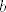 je sad trivijalno je sad trivijalno
_________________
Mario Berljafa
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
manbearpig
Forumaš(ica)


Pridružen/a: 31. 01. 2009. (19:53:28)
Postovi: (40)16
Spol: 
Lokacija: socijalno nelagodne situacije TAMO SAM
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
 Postano: 15:31 sri, 4. 2. 2009 Naslov: Postano: 15:31 sri, 4. 2. 2009 Naslov: |
    |
|
|
[quote="Milojko"]prvi zadatak.
imaš da je f=g*q+r. znaš q, i znaš r. zanima te kolko je f/q. sad podjeliš sve skupa sa q. dobiš: f/q=g+r/q. i sad podjeli ovaj r sa q. dobije se nešto plus ostatak. taj ostatak je neki r_1/q, tak ga zapišeš. i sad opet pomnoži sve skupa cijelu jednakost sa q. dobije se f=(g+"nešto što se dobilo djeljenjem r-a sa q")*q+r_1. i sad je taj polinom f zapisan u obliku f=g_1*q+r_1. g_1=g+"nešto što se dobilo djeljenjem r-a sa q". traženi ostatak je ovaj r_1.
u biti, treba podjelit r sa q i njihov ostatak je ostatak koji daje f kad se dijeli sa q.[/quote]
jesi li siguran da je takav način dobar? zašto si onaj ostatak koji se dobije pri djeljenju r sa q zapisao kao r_1/q? i ako si ga već tako zapisao, onda bi po svemu što si napisao rješenje trebalo biti taj ostatak, a to onda nije r_1 već r_1/q. ne znan, cila san zbunjena tako da možda ne vidim nešto što je očito, al ako ti se da, mogao bi napisat sve. puno tražim, al ako ti se da. :)
| Milojko (napisa): | prvi zadatak.
imaš da je f=g*q+r. znaš q, i znaš r. zanima te kolko je f/q. sad podjeliš sve skupa sa q. dobiš: f/q=g+r/q. i sad podjeli ovaj r sa q. dobije se nešto plus ostatak. taj ostatak je neki r_1/q, tak ga zapišeš. i sad opet pomnoži sve skupa cijelu jednakost sa q. dobije se f=(g+"nešto što se dobilo djeljenjem r-a sa q")*q+r_1. i sad je taj polinom f zapisan u obliku f=g_1*q+r_1. g_1=g+"nešto što se dobilo djeljenjem r-a sa q". traženi ostatak je ovaj r_1.
u biti, treba podjelit r sa q i njihov ostatak je ostatak koji daje f kad se dijeli sa q. |
jesi li siguran da je takav način dobar? zašto si onaj ostatak koji se dobije pri djeljenju r sa q zapisao kao r_1/q? i ako si ga već tako zapisao, onda bi po svemu što si napisao rješenje trebalo biti taj ostatak, a to onda nije r_1 već r_1/q. ne znan, cila san zbunjena tako da možda ne vidim nešto što je očito, al ako ti se da, mogao bi napisat sve. puno tražim, al ako ti se da. 
|
|
| [Vrh] |
|
manbearpig
Forumaš(ica)


Pridružen/a: 31. 01. 2009. (19:53:28)
Postovi: (40)16
Spol: 
Lokacija: socijalno nelagodne situacije TAMO SAM
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
|











