| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Ignorant
Gost
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 0:49 sri, 11. 2. 2009 Naslov: Postano: 0:49 sri, 11. 2. 2009 Naslov: |
    |
|
|
na prvi pogled sam rekao wow, a kako sam ja uspio dokazat da ono vrijedi onda???
e pa zato sto ono nikako ne znaci da uvijet ne vrijedi
naime ti samo imas [latex]r(AB)\leq p[/latex], a kako je [latex]n\leq p [/latex] uvijet moze vrijedit
sad ti mozda mislis da postoji slucaj u kojem je je [latex]p=10[/latex], [latex]n=8[/latex] i [latex]r(AB)=9[/latex] pa da ne vrijedi, al kao sto rekoh to ti mislis... ispada da stvarno ne postoji
ja sam dokazao da je [latex]r(AB)=min\{ a,b\}[/latex], pri cemu je [latex]r(A)=a[/latex], [latex]r(B)=b[/latex], ne kazem da mi je dobro al mislim da je, dosta mi je dugo pa mi se neda pisat, ideja je da [latex]A[/latex] i [latex]B[/latex] prikazem kao produkt kanonskih i elementarnih matrica jer znam sta se onda desava s rangom
na prvi pogled sam rekao wow, a kako sam ja uspio dokazat da ono vrijedi onda???
e pa zato sto ono nikako ne znaci da uvijet ne vrijedi
naime ti samo imas 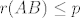 , a kako je , a kako je 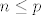 uvijet moze vrijedit uvijet moze vrijedit
sad ti mozda mislis da postoji slucaj u kojem je je 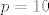 , , 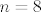 i i 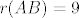 pa da ne vrijedi, al kao sto rekoh to ti mislis... ispada da stvarno ne postoji pa da ne vrijedi, al kao sto rekoh to ti mislis... ispada da stvarno ne postoji
ja sam dokazao da je 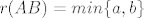 , pri cemu je , pri cemu je 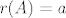 , , 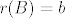 , ne kazem da mi je dobro al mislim da je, dosta mi je dugo pa mi se neda pisat, ideja je da , ne kazem da mi je dobro al mislim da je, dosta mi je dugo pa mi se neda pisat, ideja je da  i i  prikazem kao produkt kanonskih i elementarnih matrica jer znam sta se onda desava s rangom prikazem kao produkt kanonskih i elementarnih matrica jer znam sta se onda desava s rangom
_________________
Mario Berljafa
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 0:58 sri, 11. 2. 2009 Naslov: Postano: 0:58 sri, 11. 2. 2009 Naslov: |
    |
|
|
ako se to zna, nema se sta rjesavat...
al ja to neznam, al ako je to tako,
budem sutra(=za par sati) probao malo raspisat pa vitid,
onda je stvaro [latex]r(AB)=min\{ a,b\}[/latex]
ako se to zna, nema se sta rjesavat...
al ja to neznam, al ako je to tako,
budem sutra(=za par sati) probao malo raspisat pa vitid,
onda je stvaro 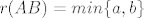
_________________
Mario Berljafa
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 13:48 sri, 11. 2. 2009 Naslov: Postano: 13:48 sri, 11. 2. 2009 Naslov: |
    |
|
|
Evo moje rješenje 2. zadatka, zapravo je slično kao markotron-ovo, ali malo ljepše napisano :P
Neka je [latex]A \in \textrm{M}_{mn}[/latex] i [latex]B \in \textrm{M}_{nk}[/latex], te neka je [latex]C=AB[/latex]. Neka je nadalje [latex]A=\left(a_{ij}\right)[/latex], [latex]B=\left(b_{ij}\right)[/latex], [latex]C=\left(c_{ij}\right)[/latex].
Vrijedi: [latex]c_{ij}=\sum\limits_{l=1}^{n}{a_{il}b_{lj}}, \quad \forall i \in \left\{1,2,\ldots,m\right\}, \forall j \in \left\{1,2,\ldots,k\right\}[/latex].
Neka je sada [latex]i \in \left\{1,2,\ldots,m\right\}[/latex] fiksan, tada je
[latex]\left(c_{i1},c_{i2},\ldots,c_{ik}\right)=\left(\sum\limits_{l=1}^{n}{a_{il}b_{l1}},\sum\limits_{l=1}^{n}{a_{il}b_{l2}},\ldots,\sum\limits_{l=1}^{n}{a_{il}b_{lk}}\right)=\sum\limits_{l=1}^{n}\left[a_{il}\left(b_{l1},b_{l2},\ldots,b_{lk}\right)\right][/latex].
Sada zaključujemo da je svaki redak matrice [latex]C[/latex] jednak nekoj linearnoj kombinaciji redaka matrice [latex]B[/latex], analognim postupkom zaključujemo sličnu tvrdnju za stupce matrice [latex]C[/latex]. Iz ovoga sada direktno slijedi tvrdnja zadatka.
Evo moje rješenje 2. zadatka, zapravo je slično kao markotron-ovo, ali malo ljepše napisano 
Neka je  i i  , te neka je , te neka je 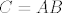 . Neka je nadalje . Neka je nadalje 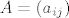 , , 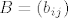 , , 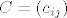 . .
Vrijedi: 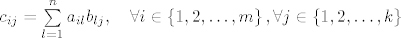 . .
Neka je sada 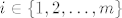 fiksan, tada je fiksan, tada je
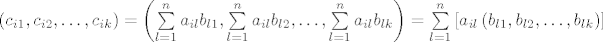 . .
Sada zaključujemo da je svaki redak matrice  jednak nekoj linearnoj kombinaciji redaka matrice jednak nekoj linearnoj kombinaciji redaka matrice  , analognim postupkom zaključujemo sličnu tvrdnju za stupce matrice , analognim postupkom zaključujemo sličnu tvrdnju za stupce matrice  . Iz ovoga sada direktno slijedi tvrdnja zadatka. . Iz ovoga sada direktno slijedi tvrdnja zadatka.
|
|
| [Vrh] |
|
|











