| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
loreal
Forumaš(ica)


Pridružen/a: 09. 02. 2008. (18:30:35)
Postovi: (33)16
Spol: 
Lokacija: sava
|
 Postano: 21:40 pon, 9. 2. 2009 Naslov: Postano: 21:40 pon, 9. 2. 2009 Naslov: |
    |
|
|
[quote="Luuka"][quote="Anonymous"]Mislila sam na prvi zadatak iz prošlogodišnje zadaće. Vidim da je u ovogodišnjoj 3. zadatak sličan, molim da mi nektko pojasni u čem je fora?! Hvala![/quote]
Ne treba baš niš raspisivat, sve čitaš iz matrice, koja je Jordanova forma... dakle:
karakt polinom je umnožak ovih na dijagonali, to je lako.
minimalni je ko karakteristični, samo paziš na potencije. Potencija u minimalnom polinomu od (lambda - lambda1) je broj blokova pridruženih sv vrijednosti lambda1... u ovom slučaju (3. iz ovogodišnje) kod 3 je potencija 1, a kod 2 je potencija 2.
d(A-2I)= dim Ker (A-2I) = geom kratnost sv vrij. 2 ,a to je (iz min polinoma) =2.
alg od 2 je potencija u karakt polinomu.
je li A dijagonalizibilan? NE, jer se razlikuju geom i alg kratnost barem jedne sv vrijednosti.
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
[quote="amorphis"]nekako mi se ne čini da je to ok [/quote]
Ni meni se ne čini ok jer si samo dokazala da je A=I jedno rješenje. Ne da je jedino što se traži... (jedino je cjelobrojno, ali ne općenito jedino)... sad možda na ovu prep iskoristit nekako da je A hermitski pa da je jedino rješenj A=I. :D[/quote]
sta nije minimalni polinom potencija ona koliko ima najvise blokova te svojstvene vrijednosti????
u 6.zad. jel zna netko kako iskoristiti uvjet d(A+I)=3, sto mi to govori o Jordanovoj formi?
thxxx :roll:
| Luuka (napisa): | | Anonymous (napisa): | | Mislila sam na prvi zadatak iz prošlogodišnje zadaće. Vidim da je u ovogodišnjoj 3. zadatak sličan, molim da mi nektko pojasni u čem je fora?! Hvala! |
Ne treba baš niš raspisivat, sve čitaš iz matrice, koja je Jordanova forma... dakle:
karakt polinom je umnožak ovih na dijagonali, to je lako.
minimalni je ko karakteristični, samo paziš na potencije. Potencija u minimalnom polinomu od (lambda - lambda1) je broj blokova pridruženih sv vrijednosti lambda1... u ovom slučaju (3. iz ovogodišnje) kod 3 je potencija 1, a kod 2 je potencija 2.
d(A-2I)= dim Ker (A-2I) = geom kratnost sv vrij. 2 ,a to je (iz min polinoma) =2.
alg od 2 je potencija u karakt polinomu.
je li A dijagonalizibilan? NE, jer se razlikuju geom i alg kratnost barem jedne sv vrijednosti.
Added after 4 minutes:
| amorphis (napisa): | | nekako mi se ne čini da je to ok |
Ni meni se ne čini ok jer si samo dokazala da je A=I jedno rješenje. Ne da je jedino što se traži... (jedino je cjelobrojno, ali ne općenito jedino)... sad možda na ovu prep iskoristit nekako da je A hermitski pa da je jedino rješenj A=I.  |
sta nije minimalni polinom potencija ona koliko ima najvise blokova te svojstvene vrijednosti????
u 6.zad. jel zna netko kako iskoristiti uvjet d(A+I)=3, sto mi to govori o Jordanovoj formi?
thxxx 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
mischa
Forumaš(ica)

Pridružen/a: 15. 09. 2007. (17:52:41)
Postovi: (D8)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:11 pon, 9. 2. 2009 Naslov: Postano: 22:11 pon, 9. 2. 2009 Naslov: |
    |
|
|
[quote="mischa"]jel uspio netko rijesiti 7? iz traga dobijem da imam dva puta -4 i cetiri puta 2, ali nikako ne uspijem iz ranga dobiti koliko imam blokova..[/quote]
r = n -d iz teorema o rangu i defektu... dakle imaš da je
d(A+4I)=1, a d(A-2I)=3.
Dakle, imaš jedan blok za -4 i 3 bloka za 2. I sad posložiš kaj imaš... 4 puta dvojku i 2 put -4 na dijagonalu, i onda kod -4 stavit 1 iznad dij (jer imaš 1 blok), i kod dvojki staviš jednu jedinicu negdje da bi dobila 3 bloka. :D
| mischa (napisa): | | jel uspio netko rijesiti 7? iz traga dobijem da imam dva puta -4 i cetiri puta 2, ali nikako ne uspijem iz ranga dobiti koliko imam blokova.. |
r = n -d iz teorema o rangu i defektu... dakle imaš da je
d(A+4I)=1, a d(A-2I)=3.
Dakle, imaš jedan blok za -4 i 3 bloka za 2. I sad posložiš kaj imaš... 4 puta dvojku i 2 put -4 na dijagonalu, i onda kod -4 stavit 1 iznad dij (jer imaš 1 blok), i kod dvojki staviš jednu jedinicu negdje da bi dobila 3 bloka. 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
mischa
Forumaš(ica)

Pridružen/a: 15. 09. 2007. (17:52:41)
Postovi: (D8)16
Spol: 
|
|
| [Vrh] |
|
loreal
Forumaš(ica)


Pridružen/a: 09. 02. 2008. (18:30:35)
Postovi: (33)16
Spol: 
Lokacija: sava
|
 Postano: 22:18 pon, 9. 2. 2009 Naslov: Postano: 22:18 pon, 9. 2. 2009 Naslov: |
    |
|
|
[quote="Luuka"][quote="loreal"]sta nije minimalni polinom potencija ona koliko ima najvise blokova te svojstvene vrijednosti????[/quote]
Ja mislim da je broj blokova geom kratnost jer svaki blok daje jedan sv vektor...
[quote="loreal"]
u 6.zad. jel zna netko kako iskoristiti uvjet d(A+I)=3, sto mi to govori o Jordanovoj formi?
thxxx :roll:[/quote]
d(A+I)=dim Ker( A+I), dakle geom kratnost, dakle broj blokova pridruženih sv vrijednosti -1 :D[/quote]
da, da, slazem se za ovu geom kratnost, to je opcenito broj blokova, a mislila sam na pitanje da najveca klijetka neke svojstvene vrijednosti je potencija min. pol. za tu svojst.vrijednost? slazes li se?hm...
i hvala za odg defekta :D
| Luuka (napisa): | | loreal (napisa): | | sta nije minimalni polinom potencija ona koliko ima najvise blokova te svojstvene vrijednosti???? |
Ja mislim da je broj blokova geom kratnost jer svaki blok daje jedan sv vektor...
| loreal (napisa): |
u 6.zad. jel zna netko kako iskoristiti uvjet d(A+I)=3, sto mi to govori o Jordanovoj formi?
thxxx  |
d(A+I)=dim Ker( A+I), dakle geom kratnost, dakle broj blokova pridruženih sv vrijednosti -1  |
da, da, slazem se za ovu geom kratnost, to je opcenito broj blokova, a mislila sam na pitanje da najveca klijetka neke svojstvene vrijednosti je potencija min. pol. za tu svojst.vrijednost? slazes li se?hm...
i hvala za odg defekta 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 22:22 pon, 9. 2. 2009 Naslov: Postano: 22:22 pon, 9. 2. 2009 Naslov: |
    |
|
|
[quote="loreal"]
da, da, slazem se za ovu geom kratnost, to je opcenito broj blokova, a mislila sam na pitanje da najveca klijetka neke svojstvene vrijednosti je potencija min. pol. za tu svojst.vrijednost? slazes li se?hm...
[/quote]
Mislim da si u pravu, da sam fulo tamo negdje gore kod isčitavanja iz Jordanove forme (3.zad), popravim sad...
dakle rezime (nek netko ispravi ako nije dobro, ili potvrdi ako je dobro):
broj blokova = geom kratnost
dim najvećeg bloka = potencija u min polinomu
| loreal (napisa): |
da, da, slazem se za ovu geom kratnost, to je opcenito broj blokova, a mislila sam na pitanje da najveca klijetka neke svojstvene vrijednosti je potencija min. pol. za tu svojst.vrijednost? slazes li se?hm...
|
Mislim da si u pravu, da sam fulo tamo negdje gore kod isčitavanja iz Jordanove forme (3.zad), popravim sad...
dakle rezime (nek netko ispravi ako nije dobro, ili potvrdi ako je dobro):
broj blokova = geom kratnost
dim najvećeg bloka = potencija u min polinomu
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
 Postano: 23:35 pon, 9. 2. 2009 Naslov: Postano: 23:35 pon, 9. 2. 2009 Naslov: |
    |
|
|
[quote="amorphis"]
ima li tko ideju i prijedlog za 13? da li se može uzet supstitucija (npr x= A) i
onda se gleda jednakost x^9+x^7+x^5+x^3=4 i cjelobrojne nultočke se
odrede kao djelitelji slobodnog faktora (dakle 4) što može biti 1, -1, 2, -2, 4
i -4, jedino x=1 zadovoljava, odnosno A=I, nekako mi se ne čini da je to
ok jer se nigdje ne koristi činjenica da je A hermitski...[/quote]
Ja sam to slično kao u vjezbama..
A herm akko A*=A akko A*(e)=A(e) akko lambda(i)=konjugirano(lambda(i)), za svaki i=1, ..., n,, sto znaci da je lambda(i) iz R.
e sad.. f(lambda)=...
f(A)=0
iz lambda iz spektra --> f(lambda)=0
Vidimo da je f(1)=0, nadjemo derivaciju od f, i vidimo da je >=0, za sve lambda iz R --> f je rastuca na R --> 1 je jedina nultocka fje f na R --> 1 je iz spektra.
Sad je A(e)= (1 na dijagonali, 0 okolo) --> A=I
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
[quote="Luuka"]
broj blokova = geom kratnost
dim najvećeg bloka = potencija u min polinomu[/quote]
dobro ti je to :) , i jos cu dodati:
zbroj dim klijetki=potencija u karakt. polinomu..
| amorphis (napisa): |
ima li tko ideju i prijedlog za 13? da li se može uzet supstitucija (npr x= A) i
onda se gleda jednakost x^9+x^7+x^5+x^3=4 i cjelobrojne nultočke se
odrede kao djelitelji slobodnog faktora (dakle 4) što može biti 1, -1, 2, -2, 4
i -4, jedino x=1 zadovoljava, odnosno A=I, nekako mi se ne čini da je to
ok jer se nigdje ne koristi činjenica da je A hermitski... |
Ja sam to slično kao u vjezbama..
A herm akko A*=A akko A*(e)=A(e) akko lambda(i)=konjugirano(lambda(i)), za svaki i=1, ..., n,, sto znaci da je lambda(i) iz R.
e sad.. f(lambda)=...
f(A)=0
iz lambda iz spektra → f(lambda)=0
Vidimo da je f(1)=0, nadjemo derivaciju od f, i vidimo da je >=0, za sve lambda iz R → f je rastuca na R → 1 je jedina nultocka fje f na R → 1 je iz spektra.
Sad je A(e)= (1 na dijagonali, 0 okolo) → A=I
Added after 4 minutes:
| Luuka (napisa): |
broj blokova = geom kratnost
dim najvećeg bloka = potencija u min polinomu |
dobro ti je to  , i jos cu dodati: , i jos cu dodati:
zbroj dim klijetki=potencija u karakt. polinomu..
_________________
..a jooooooj..
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Goran
Forumaš(ica)

Pridružen/a: 02. 07. 2003. (16:03:48)
Postovi: (2C)16
Spol: 
|
|
| [Vrh] |
|
mischa
Forumaš(ica)

Pridružen/a: 15. 09. 2007. (17:52:41)
Postovi: (D8)16
Spol: 
|
 Postano: 23:02 uto, 10. 2. 2009 Naslov: Postano: 23:02 uto, 10. 2. 2009 Naslov: |
    |
|
|
ja sam u 10. zad dobila ova rjesenja:
E1= {(1/sqrt2,0),(0,-1/sqrt2)}
B2= {(1,1),(1,1)}
E2= {(1/2,1/2),(1/2,1/2)}
B3= {(1/4,-1/4),(-1/4,1/4)}
E3= {(1,-1),(-1,1)}
jel tko dobio ovakva rjesenja ili sam pogrijesila negdje u racunanju?
ja sam u 10. zad dobila ova rjesenja:
E1= {(1/sqrt2,0),(0,-1/sqrt2)}
B2= {(1,1),(1,1)}
E2= {(1/2,1/2),(1/2,1/2)}
B3= {(1/4,-1/4),(-1/4,1/4)}
E3= {(1,-1),(-1,1)}
jel tko dobio ovakva rjesenja ili sam pogrijesila negdje u racunanju?
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
 Postano: 23:35 uto, 10. 2. 2009 Naslov: Postano: 23:35 uto, 10. 2. 2009 Naslov: |
    |
|
|
[quote="mischa"]ja sam u 10. zad dobila ova rjesenja:
E1= {(1/sqrt2,0),(0,-1/sqrt2)}
B2= {(1,1),(1,1)}
E2= {(1/2,1/2),(1/2,1/2)}
B3= {(1/4,-1/4),(-1/4,1/4)}
E3= {(1,-1),(-1,1)}
jel tko dobio ovakva rjesenja ili sam pogrijesila negdje u racunanju?[/quote]
Ja sam sve osim E3 dobila isto, E3={(1/2, -1/2), (-1/2, 1/2)}
Jos da pitam, kad se trazi matrica operatora f(A)=..., s tim da mat A imamo zadanu, da li se za svojstvene vrijednosti uvrštava f(-lambda) ili f(lambda), a bilj pise prvo, a u tm-u 2., pa mi nije jasno sta je dobro.. :?
Meni jos fale 4, 5, 11. Pomazite!! :)
| mischa (napisa): | ja sam u 10. zad dobila ova rjesenja:
E1= {(1/sqrt2,0),(0,-1/sqrt2)}
B2= {(1,1),(1,1)}
E2= {(1/2,1/2),(1/2,1/2)}
B3= {(1/4,-1/4),(-1/4,1/4)}
E3= {(1,-1),(-1,1)}
jel tko dobio ovakva rjesenja ili sam pogrijesila negdje u racunanju? |
Ja sam sve osim E3 dobila isto, E3={(1/2, -1/2), (-1/2, 1/2)}
Jos da pitam, kad se trazi matrica operatora f(A)=..., s tim da mat A imamo zadanu, da li se za svojstvene vrijednosti uvrštava f(-lambda) ili f(lambda), a bilj pise prvo, a u tm-u 2., pa mi nije jasno sta je dobro.. 
Meni jos fale 4, 5, 11. Pomazite!! 
_________________
..a jooooooj..
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:46 sri, 11. 2. 2009 Naslov: Postano: 0:46 sri, 11. 2. 2009 Naslov: |
    |
|
|
5. zadatak je krivo zadan, tj. ne postoji matrica koja ima karakteristični polinom [latex]k_{A}(\lambda)=-(\lambda - 1)^{5}(\lambda +1)^{5}[/latex]. Ako se htjelo reći [latex]k_{A}(\lambda)=(\lambda - 1)^{5}(\lambda +1)^{5}[/latex], onda bi rješenje trebalo biti matrica 10x10 td:
1) na dijagonali ima zaredom pet 1 pa pet -1 (vidimo iz karakterističnog)
2) najveći blok sv. vr. 1 je dimenzije 4 (vidimo iz minimalnog) pa, budući da ih ima 5, jedino može biti jedan blok dim. 4 i jedan dim. 1. Također vidimo da je najveći blok sv. vr. -1 jednak 2. Dakle može biti 2+2+1, ili 2+1+1+1.
3) u zadatku je dana geometrijska kratnost sv. vr. -1, znači ima 3 bloka koja pripadaju sv. vr. -1. Dakle može biti samo 2+2+1.
Nadam se da je to to.
5. zadatak je krivo zadan, tj. ne postoji matrica koja ima karakteristični polinom 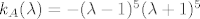 . Ako se htjelo reći . Ako se htjelo reći  , onda bi rješenje trebalo biti matrica 10x10 td: , onda bi rješenje trebalo biti matrica 10x10 td:
1) na dijagonali ima zaredom pet 1 pa pet -1 (vidimo iz karakterističnog)
2) najveći blok sv. vr. 1 je dimenzije 4 (vidimo iz minimalnog) pa, budući da ih ima 5, jedino može biti jedan blok dim. 4 i jedan dim. 1. Također vidimo da je najveći blok sv. vr. -1 jednak 2. Dakle može biti 2+2+1, ili 2+1+1+1.
3) u zadatku je dana geometrijska kratnost sv. vr. -1, znači ima 3 bloka koja pripadaju sv. vr. -1. Dakle može biti samo 2+2+1.
Nadam se da je to to.
|
|
| [Vrh] |
|
Goran
Forumaš(ica)

Pridružen/a: 02. 07. 2003. (16:03:48)
Postovi: (2C)16
Spol: 
|
 Postano: 0:58 sri, 11. 2. 2009 Naslov: Postano: 0:58 sri, 11. 2. 2009 Naslov: |
    |
|
|
[quote="rafaelm"]5. zadatak je krivo zadan, tj. ne postoji matrica koja ima karakteristični polinom [latex]k_{A}(\lambda)=-(\lambda - 1)^{5}(\lambda +1)^{5}[/latex]. Ako se htjelo reći [latex]k_{A}(\lambda)=(\lambda - 1)^{5}(\lambda +1)^{5}[/latex], onda bi rješenje trebalo biti matrica 10x10 td:
1) na dijagonali ima zaredom pet 1 pa pet -1 (vidimo iz karakterističnog)
2) najveći blok sv. vr. 1 je dimenzije 4 (vidimo iz minimalnog) pa, budući da ih ima 5, jedino može biti jedan blok dim. 4 i jedan dim. 1. Također vidimo da je najveći blok sv. vr. -1 jednak 2. Dakle može biti 2+2+1, ili 2+1+1+1.
3) u zadatku je dana geometrijska kratnost sv. vr. -1, znači ima 3 bloka koja pripadaju sv. vr. -1. Dakle može biti samo 2+2+1.
Nadam se da je to to.[/quote]
To je 6. zadatak :) .
| rafaelm (napisa): | 5. zadatak je krivo zadan, tj. ne postoji matrica koja ima karakteristični polinom 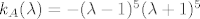 . Ako se htjelo reći . Ako se htjelo reći  , onda bi rješenje trebalo biti matrica 10x10 td: , onda bi rješenje trebalo biti matrica 10x10 td:
1) na dijagonali ima zaredom pet 1 pa pet -1 (vidimo iz karakterističnog)
2) najveći blok sv. vr. 1 je dimenzije 4 (vidimo iz minimalnog) pa, budući da ih ima 5, jedino može biti jedan blok dim. 4 i jedan dim. 1. Također vidimo da je najveći blok sv. vr. -1 jednak 2. Dakle može biti 2+2+1, ili 2+1+1+1.
3) u zadatku je dana geometrijska kratnost sv. vr. -1, znači ima 3 bloka koja pripadaju sv. vr. -1. Dakle može biti samo 2+2+1.
Nadam se da je to to. |
To je 6. zadatak  . .
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Ančica
Forumaš(ica)


Pridružen/a: 01. 12. 2006. (16:12:53)
Postovi: (F6)16
Spol: 
|
|
| [Vrh] |
|
mischa
Forumaš(ica)

Pridružen/a: 15. 09. 2007. (17:52:41)
Postovi: (D8)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 11:26 sri, 11. 2. 2009 Naslov: Re: help Postano: 11:26 sri, 11. 2. 2009 Naslov: Re: help |
    |
|
|
[quote="Anonymous"]Jel zna netko kako izračunti tr((A-I)^100) ako je minimalni polinom (lambda+3)^4, a karakteristični polinom (lambda+3)^8?[/quote]
Dakle, prvo što nam treba je da je trag neovisan o bazi... to vrijedi jer je
tr(A)=tr(S*J*S^-1)=tr(S*S^-1*J)=tr(J). :D
dimA=8 iz karakt polinoma.
Sad gledamo u toj bazi (jordanovoj) što se dođađa sa (A-I)^100...
jordanova matrica od A ima -3 na dijagonali, i ponegdje jedinice na sporednoj dijagonali.
A-I ima -4 na dijagonali i negdje jedinice iznad dijagonale. Kad to bacimo na 100-tu, na dijagonali će ostat 4^100, a ovo van dijagonale će nestat (a i nije nam to nešto bitno za ovaj zadatak)...
dakle, kad pozbrajamo dijagonalu imamo 8*4^100 = 4^102 :D
| Anonymous (napisa): | | Jel zna netko kako izračunti tr((A-I)^100) ako je minimalni polinom (lambda+3)^4, a karakteristični polinom (lambda+3)^8? |
Dakle, prvo što nam treba je da je trag neovisan o bazi... to vrijedi jer je
tr(A)=tr(S*J*S^-1)=tr(S*S^-1*J)=tr(J). 
dimA=8 iz karakt polinoma.
Sad gledamo u toj bazi (jordanovoj) što se dođađa sa (A-I)^100...
jordanova matrica od A ima -3 na dijagonali, i ponegdje jedinice na sporednoj dijagonali.
A-I ima -4 na dijagonali i negdje jedinice iznad dijagonale. Kad to bacimo na 100-tu, na dijagonali će ostat 4^100, a ovo van dijagonale će nestat (a i nije nam to nešto bitno za ovaj zadatak)...
dakle, kad pozbrajamo dijagonalu imamo 8*4^100 = 4^102 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|






















