| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 16:08 sri, 11. 2. 2009 Naslov: Re: pitanjce Postano: 16:08 sri, 11. 2. 2009 Naslov: Re: pitanjce |
    |
|
|
[quote="Anonymous"]kako su povezani inverzi od a i a transponirano....matrica je regularna........[/quote]
[latex] A \cdot A^{-1}=I[/latex] , kad to transponiramo dobijemo:
[latex] (A^{-1})^t \cdot A^t=I[/latex], dakle inverz od At je transponirani A^-1. (kad se ista stvar ponovi na [latex] A^{-1} \cdot A=I[/latex] )
[quote="Anonymous"]što sve mogu raditi u "matričnim jednađbama"....to je moj naziv dada :D znam da mogu množiti sa A na minus prvu ako je A regularna.....izlučivati? što još.....koja svojstva vrijede?[/quote]
Možeš množiti slijeva i s desna (oprez s koje strane) sa ne-nul matricama (možeš i sa nul al to nema smisla), dodavati, oduzimati matrice sa svake strane, množiti sve skalarom različitim od nule, koristiti sva svojstva matrica (asoc i sl)... svašta možeš :D
| Anonymous (napisa): | | kako su povezani inverzi od a i a transponirano....matrica je regularna........ |
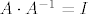 , kad to transponiramo dobijemo: , kad to transponiramo dobijemo:
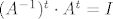 , dakle inverz od At je transponirani A^-1. (kad se ista stvar ponovi na , dakle inverz od At je transponirani A^-1. (kad se ista stvar ponovi na 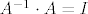 ) )
| Anonymous (napisa): | što sve mogu raditi u "matričnim jednađbama"....to je moj naziv dada  znam da mogu množiti sa A na minus prvu ako je A regularna.....izlučivati? što još.....koja svojstva vrijede? znam da mogu množiti sa A na minus prvu ako je A regularna.....izlučivati? što još.....koja svojstva vrijede? |
Možeš množiti slijeva i s desna (oprez s koje strane) sa ne-nul matricama (možeš i sa nul al to nema smisla), dodavati, oduzimati matrice sa svake strane, množiti sve skalarom različitim od nule, koristiti sva svojstva matrica (asoc i sl)... svašta možeš 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
lorozic
Forumaš(ica)

Pridružen/a: 08. 12. 2008. (17:11:14)
Postovi: (50)16
Spol: 
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
lorozic
Forumaš(ica)

Pridružen/a: 08. 12. 2008. (17:11:14)
Postovi: (50)16
Spol: 
|
|
| [Vrh] |
|
teja
Forumaš(ica)


Pridružen/a: 14. 07. 2006. (15:34:28)
Postovi: (14A)16
Spol: 
Lokacija: zg-ma and back
|
|
| [Vrh] |
|
maloka
Forumaš(ica)

Pridružen/a: 05. 02. 2009. (22:00:18)
Postovi: (32)16
|
 Postano: 18:29 sri, 11. 2. 2009 Naslov: Postano: 18:29 sri, 11. 2. 2009 Naslov: |
    |
|
|
hm..to gradivo smo obradili još prije prvog kolokvija pa si prelistaj bilježnice...uglavnom...imaš za L={(x1,x2,x3,x4,x5,x6)} i vrijedi x1-x2-x3-x4-x5-x6=0, napišeš jedan od njih pomoću ostalih..npr : x1=x2+x3+x4+x5+x6. sada dobiješ da je (x1,x2,x3,x4,x5,x6)= (x2+x3+x4+x5+x6,x2,x3,x4,x5,x6) rastaviš po svakom od njih i još ga izvučeš van...i dobiješ : (x1,x2,x3,x4,x5,x6) = (1,1,0,0,0,0)x2 + (1,0,1,0,0,0)x3 + (1,0,0,1,0,0)x4 + (1,0,0,0,1,0)x5 + (1,0,0,0,0,1)x6. znaš da je to sistem izvodnica i onda još provjeriš da je lin nez i (ako nije reduciraš ga do lin nez skupa) i to ti je baza za L. Ista priča i za M. Tad imaš baze za M i L. Bazu za L+M tražiš tako da obje baze tako reći potrpaš u isti skup i reduciraš ga do lin nez skupa.Tako imaš i bazu za L+M. Zatim imaš formulu koja kaže: dim (L+M)=dimM+dimL-dim(LpresjekM). Bar ja mislim da tako ide.Ako je krivo nadam se da će netko ubrzo ispravit greške. Na zadnjim demonstraturama što sam bila,sam pitala jel postoji mogućnost da dobijemo u kolokviju nešto što je bilo obuhvaćeno u prošlom i rekla je da je moguće..tako da...
hm..to gradivo smo obradili još prije prvog kolokvija pa si prelistaj bilježnice...uglavnom...imaš za L={(x1,x2,x3,x4,x5,x6)} i vrijedi x1-x2-x3-x4-x5-x6=0, napišeš jedan od njih pomoću ostalih..npr : x1=x2+x3+x4+x5+x6. sada dobiješ da je (x1,x2,x3,x4,x5,x6)= (x2+x3+x4+x5+x6,x2,x3,x4,x5,x6) rastaviš po svakom od njih i još ga izvučeš van...i dobiješ : (x1,x2,x3,x4,x5,x6) = (1,1,0,0,0,0)x2 + (1,0,1,0,0,0)x3 + (1,0,0,1,0,0)x4 + (1,0,0,0,1,0)x5 + (1,0,0,0,0,1)x6. znaš da je to sistem izvodnica i onda još provjeriš da je lin nez i (ako nije reduciraš ga do lin nez skupa) i to ti je baza za L. Ista priča i za M. Tad imaš baze za M i L. Bazu za L+M tražiš tako da obje baze tako reći potrpaš u isti skup i reduciraš ga do lin nez skupa.Tako imaš i bazu za L+M. Zatim imaš formulu koja kaže: dim (L+M)=dimM+dimL-dim(LpresjekM). Bar ja mislim da tako ide.Ako je krivo nadam se da će netko ubrzo ispravit greške. Na zadnjim demonstraturama što sam bila,sam pitala jel postoji mogućnost da dobijemo u kolokviju nešto što je bilo obuhvaćeno u prošlom i rekla je da je moguće..tako da...
|
|
| [Vrh] |
|
lorozic
Forumaš(ica)

Pridružen/a: 08. 12. 2008. (17:11:14)
Postovi: (50)16
Spol: 
|
|
| [Vrh] |
|
tomitza
Forumaš(ica)


Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
|
| [Vrh] |
|
uzorni student
Forumaš(ica)

Pridružen/a: 24. 01. 2009. (16:11:39)
Postovi: (2C)16
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
maloka
Forumaš(ica)

Pridružen/a: 05. 02. 2009. (22:00:18)
Postovi: (32)16
|
 Postano: 19:36 sri, 11. 2. 2009 Naslov: Postano: 19:36 sri, 11. 2. 2009 Naslov: |
    |
|
|
piše mu u zadatku da su matrice istog reda i kvadratne tako da kad se transponiraju i dalje se mogu zbrajati. S obzirom da vrijedi da je r(A) = r(At) mislim da bi trebalo vrijediti onda i r(A+Bt)=r(At+B) jer se transponiranjem matricama neće promijeniti rang, nisam sigurna. ali ako to vrijedi onda bi trebalo vrijediti i s minusom. možeš A-Bt napisati kao A+Bt (ali kod B promijeniš svima predznak) i to se onda opet svodi za zbroj, jer ni u početnom zadatku s + nije ti nigdje rečeno kakvi su a(i,j) i b(i,j) oni mogu biti i negativni...ako uzmeš (A+Bt) i to nazoveš matricom C, kad transponiraš C dobiješ Ct koja je zapravo At + B, a pošto vrijedi r(C)=r(Ct) vrijedi i to gore.
piše mu u zadatku da su matrice istog reda i kvadratne tako da kad se transponiraju i dalje se mogu zbrajati. S obzirom da vrijedi da je r(A) = r(At) mislim da bi trebalo vrijediti onda i r(A+Bt)=r(At+B) jer se transponiranjem matricama neće promijeniti rang, nisam sigurna. ali ako to vrijedi onda bi trebalo vrijediti i s minusom. možeš A-Bt napisati kao A+Bt (ali kod B promijeniš svima predznak) i to se onda opet svodi za zbroj, jer ni u početnom zadatku s + nije ti nigdje rečeno kakvi su a(i,j) i b(i,j) oni mogu biti i negativni...ako uzmeš (A+Bt) i to nazoveš matricom C, kad transponiraš C dobiješ Ct koja je zapravo At + B, a pošto vrijedi r(C)=r(Ct) vrijedi i to gore.
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
Anja
Forumaš(ica)


Pridružen/a: 24. 03. 2003. (10:51:07)
Postovi: (132)16
|
|
| [Vrh] |
|
Gosjt
Gost
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Anja
Forumaš(ica)


Pridružen/a: 24. 03. 2003. (10:51:07)
Postovi: (132)16
|
|
| [Vrh] |
|
lorozic
Forumaš(ica)

Pridružen/a: 08. 12. 2008. (17:11:14)
Postovi: (50)16
Spol: 
|
|
| [Vrh] |
|
|














