| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
 Postano: 17:52 ned, 22. 2. 2009 Naslov: Postano: 17:52 ned, 22. 2. 2009 Naslov: |
    |
|
|
cujes, iskreno, i ja bi ga zaobilazila da sam sve dala,
kao sto je vecina onih koji su odg linearnu prosli tjedan. :)
ja sam cula da je pitao Binet-Cauchyev teorem, determinantu, potprostore.
to je sve sto ja znam.
p.s. jel bi mi netko mogao pomoc?
ako je A regularna kvadratna matrica donjetrokutasta, onda je i A^(-1) tj. inverz donjetrokutasa. (i ako A ima 1 na diag, i A^(-1) ima 1 na diag)
znam da se nesto treba gledat clanove adjunkte, ali... :(
pliz...
cujes, iskreno, i ja bi ga zaobilazila da sam sve dala,
kao sto je vecina onih koji su odg linearnu prosli tjedan. 
ja sam cula da je pitao Binet-Cauchyev teorem, determinantu, potprostore.
to je sve sto ja znam.
p.s. jel bi mi netko mogao pomoc?
ako je A regularna kvadratna matrica donjetrokutasta, onda je i A^(-1) tj. inverz donjetrokutasa. (i ako A ima 1 na diag, i A^(-1) ima 1 na diag)
znam da se nesto treba gledat clanove adjunkte, ali... 
pliz...
|
|
| [Vrh] |
|
uzorni student
Forumaš(ica)

Pridružen/a: 24. 01. 2009. (16:11:39)
Postovi: (2C)16
|
 Postano: 23:44 ned, 22. 2. 2009 Naslov: Postano: 23:44 ned, 22. 2. 2009 Naslov: |
    |
|
|
[quote="mycky1111"]cujes, iskreno, i ja bi ga zaobilazila da sam sve dala,
kao sto je vecina onih koji su odg linearnu prosli tjedan. :)
ja sam cula da je pitao Binet-Cauchyev teorem, determinantu, potprostore.
to je sve sto ja znam.
p.s. jel bi mi netko mogao pomoc?
ako je A regularna kvadratna matrica donjetrokutasta, onda je i A^(-1) tj. inverz donjetrokutasa. (i ako A ima 1 na diag, i A^(-1) ima 1 na diag)
znam da se nesto treba gledat clanove adjunkte, ali... :(
pliz...[/quote] ja mislim da je jer znamo da je A regularna donjetrokutasta i da je I regularna.... e sad regularna i je i nije donjetrokutasta... ona je u stvari dijagonalna ali ima isto svojstvo kao donjetrokutasta. ugl.. ako uzmemo da je i I donjetrokutasta... onda ti vrijedi ona propozicija da je umnožak dviju donjetrokustastih matrica donjetrokutasta... A pomnoženo sa A^(-1) daje I.... A i I su donjetrokutaste... znači da i inverz mora biti d.t. prema propoziciji.... al to sam ja ovak odoka izmislio...
| mycky1111 (napisa): | cujes, iskreno, i ja bi ga zaobilazila da sam sve dala,
kao sto je vecina onih koji su odg linearnu prosli tjedan. 
ja sam cula da je pitao Binet-Cauchyev teorem, determinantu, potprostore.
to je sve sto ja znam.
p.s. jel bi mi netko mogao pomoc?
ako je A regularna kvadratna matrica donjetrokutasta, onda je i A^(-1) tj. inverz donjetrokutasa. (i ako A ima 1 na diag, i A^(-1) ima 1 na diag)
znam da se nesto treba gledat clanove adjunkte, ali... 
pliz... |
ja mislim da je jer znamo da je A regularna donjetrokutasta i da je I regularna.... e sad regularna i je i nije donjetrokutasta... ona je u stvari dijagonalna ali ima isto svojstvo kao donjetrokutasta. ugl.. ako uzmemo da je i I donjetrokutasta... onda ti vrijedi ona propozicija da je umnožak dviju donjetrokustastih matrica donjetrokutasta... A pomnoženo sa A^(-1) daje I.... A i I su donjetrokutaste... znači da i inverz mora biti d.t. prema propoziciji.... al to sam ja ovak odoka izmislio...
_________________
zrno po zrno pogača... piva po piva povraća
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
baloncic
Forumaš s poteškoćama u pisanju


Pridružen/a: 11. 10. 2008. (03:46:21)
Postovi: (23)16
Spol: 
Lokacija: Destination unknown
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
 Postano: 20:25 pon, 23. 2. 2009 Naslov: Postano: 20:25 pon, 23. 2. 2009 Naslov: |
    |
|
|
Za grupu M-Ž, ovaj tjedan raspored (i rezultati) je kako slijedi:
utorak, 24.2. (203)
11:00 Mia Primorac (7), Marina Slišković (10), Martina Pehar (4), Antonia Perkušić (3)
12:00 Tomislav Paj (8 ), Martina Tepić (5), Magdalena Mikulić (5), Ivo Matijašević (6)
13:00 Lovro Rožić (7), Marko Vindiš (6), Miloš Trifunović (11), Sven Majerić (9*)
***** Irena Malović (1/5*), Ilija Marković (0/4*)
srijeda, 25.2. (108)
16:00 Maja Trpčić (7), Tomislav Matulić (6), Tomislav Maruščak (5), Milan Nikolić (5)
17:00 Marija Pijević (4), Božidar Ševo (3), Dijana Marinčić (10*)
****** Martina Soldo (-1/12*)
četvrtak, 26.2. (110)
11:00 Lidija Škuflić (3), Maja Šekoranja (6), Damjan Pištalo (10), Andrija Štajduhar (7)
12:00 Damjan Murković (10), Jasmina Redžić (4), Anthea Štor (7)
13:00 Marija Tepšić (3), Petra Vukašinović (6), Tea Poturica (3), Ana Vidaček (6)
Studenti:
Dino Pavić (5), Marijana Vukoja (4), Tomislav Smetko (3), Marta Topić (5) i Amalija Oršolić (7)
su izrazili želju da odgovaraju sljedeći tjedan. Ako se predomisle, mogu mi se javiti.
Ostali studenti NISU ostvarili BAREM +3 boda (ne +4, nego +3 :-).
Studenti koji su ostvarili prag prvi puta, mogu odgovarati ovaj tjedan.
To su bodovi sa * (zvjezdica); neki od njih su na gornjem popisu, ali ako
žele, mogu jednostavno ne doći na ispit (jer su na kraju posljednjeg termina).
Ostali mogu izabrati jedan od tih termina.
Podsjećam da se usmeno može odgovarati najviše DVAPUT.
Pisati možete i triput :-)
- Nenad Antonić
Za grupu M-Ž, ovaj tjedan raspored (i rezultati) je kako slijedi:
utorak, 24.2. (203)
11:00 Mia Primorac (7), Marina Slišković (10), Martina Pehar (4), Antonia Perkušić (3)
12:00 Tomislav Paj (8 ), Martina Tepić (5), Magdalena Mikulić (5), Ivo Matijašević (6)
13:00 Lovro Rožić (7), Marko Vindiš (6), Miloš Trifunović (11), Sven Majerić (9*)
***** Irena Malović (1/5*), Ilija Marković (0/4*)
srijeda, 25.2. (108)
16:00 Maja Trpčić (7), Tomislav Matulić (6), Tomislav Maruščak (5), Milan Nikolić (5)
17:00 Marija Pijević (4), Božidar Ševo (3), Dijana Marinčić (10*)
****** Martina Soldo (-1/12*)
četvrtak, 26.2. (110)
11:00 Lidija Škuflić (3), Maja Šekoranja (6), Damjan Pištalo (10), Andrija Štajduhar (7)
12:00 Damjan Murković (10), Jasmina Redžić (4), Anthea Štor (7)
13:00 Marija Tepšić (3), Petra Vukašinović (6), Tea Poturica (3), Ana Vidaček (6)
Studenti:
Dino Pavić (5), Marijana Vukoja (4), Tomislav Smetko (3), Marta Topić (5) i Amalija Oršolić (7)
su izrazili želju da odgovaraju sljedeći tjedan. Ako se predomisle, mogu mi se javiti.
Ostali studenti NISU ostvarili BAREM +3 boda (ne +4, nego +3  . .
Studenti koji su ostvarili prag prvi puta, mogu odgovarati ovaj tjedan.
To su bodovi sa * (zvjezdica); neki od njih su na gornjem popisu, ali ako
žele, mogu jednostavno ne doći na ispit (jer su na kraju posljednjeg termina).
Ostali mogu izabrati jedan od tih termina.
Podsjećam da se usmeno može odgovarati najviše DVAPUT.
Pisati možete i triput 
- Nenad Antonić
Zadnja promjena: nenad; 21:24 pon, 23. 2. 2009; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
mmvvooll
Forumaš(ica)

Pridružen/a: 21. 02. 2009. (19:16:06)
Postovi: (16)16
|
|
| [Vrh] |
|
bozidarsevo
Forumaš(ica)


Pridružen/a: 17. 09. 2008. (10:15:01)
Postovi: (1D1)16
Spol: 
Lokacija: Samobor
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
 Postano: 21:57 pon, 23. 2. 2009 Naslov: Postano: 21:57 pon, 23. 2. 2009 Naslov: |
    |
|
|
prof je danas rekao da je u ponedjeljak vjerojatno zadnji termin pismenog dijela usmenog, i da ce mozda bit malo kasnije nego inace jer pocinje nastava.
i opet ce se pisat pismeni dio, ali bez eliminacijskog dijela, vec nesto kratko, vrlo vjerojatno slicno drugom dijelu ovih testova do sada(nesto dokazat, napisat, neki teorijski zadacic)...
i mislim da na to MORAJU izaci i oni s popravnih (jer to vam je zadnja sansa za la1)
ali, pitajte prof... :D
prof je danas rekao da je u ponedjeljak vjerojatno zadnji termin pismenog dijela usmenog, i da ce mozda bit malo kasnije nego inace jer pocinje nastava.
i opet ce se pisat pismeni dio, ali bez eliminacijskog dijela, vec nesto kratko, vrlo vjerojatno slicno drugom dijelu ovih testova do sada(nesto dokazat, napisat, neki teorijski zadacic)...
i mislim da na to MORAJU izaci i oni s popravnih (jer to vam je zadnja sansa za la1)
ali, pitajte prof... 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 22:43 pon, 23. 2. 2009 Naslov: Postano: 22:43 pon, 23. 2. 2009 Naslov: |
    |
|
|
[quote="mycky1111"]ako je A regularna kvadratna matrica donjetrokutasta, onda je i A^(-1) tj. inverz donjetrokutasa. (i ako A ima 1 na diag, i A^(-1) ima 1 na diag)
znam da se nesto treba gledat clanove adjunkte[/quote]
neka je [latex]A=[a_{ij}]\in \textrm{M}_n[/latex], neka je [latex]X=[x_{ij}]\in \texrm{M}_n[/latex] adjunkta od [latex]A[/latex], dakle [latex]x_{ij}=A_{ji}, \forall i,j\in \{ 1,2,...,n\}[/latex]
[latex]a_{ij}=0, \forall i,j \in \{ 1,2,...,n\} ,i<j[/latex]
zelimo pokazat da je [latex]x_{ij}=0, \forall i,j \in \{ 1,2,...,n\} ,i<j[/latex]
neka je dakle [latex]i,j \in \{ 1,2,...,n\} ,j<i[/latex]
[latex]x_{ji}=A_{ij}[/latex]
[latex]A_{ij}=(-1)^{i+j}\delta_{ij}[/latex], pri cemu je [latex]\delta_{ij}[/latex] determinanta matrice koja nastaje od [latex]A[/latex] tako da uklonimo [latex]i[/latex]-ti redak i [latex]j[/latex]-ti stupac, jasno je opet imamo donjetrokutastu matricu, dakle determinanta je umnozak elemenata na dijagonali [latex]\delta_{ij}=a_{11}a_{22}...a_{j-1,j-1}a_{j,j+1}...a_{i-1,i}a_{i+1,i+1}...a_{nn}=0[/latex] jer je npr. [latex]a_{j,j+1}=0[/latex]
za ovu drugu tvrdnju znamo da je [latex]\displaystyle A\cdot \frac{1}{\textrm{det}A}X=I[/latex], lako se vidi da kod mnozenja (donje)trokutastih matrica na dijagonalnim mjestima imamo bas umnozak koeficijenata na istim dijagonalnim mjestima od polaznih matrica.... [i]ja i objasnjavanje[/i]... od tud slijedi tvrdnja, jer [latex]I[/latex] ima na svim dijagonalnim mjestima [latex]1[/latex], pa ako na nekom ima [latex]A[/latex] mora imat i inverz
| mycky1111 (napisa): | ako je A regularna kvadratna matrica donjetrokutasta, onda je i A^(-1) tj. inverz donjetrokutasa. (i ako A ima 1 na diag, i A^(-1) ima 1 na diag)
znam da se nesto treba gledat clanove adjunkte |
neka je 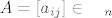 , neka je , neka je 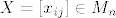 adjunkta od adjunkta od  , dakle , dakle 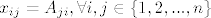
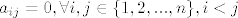
zelimo pokazat da je 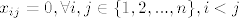
neka je dakle 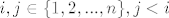

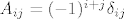 , pri cemu je , pri cemu je 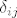 determinanta matrice koja nastaje od determinanta matrice koja nastaje od  tako da uklonimo tako da uklonimo  -ti redak i -ti redak i 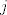 -ti stupac, jasno je opet imamo donjetrokutastu matricu, dakle determinanta je umnozak elemenata na dijagonali -ti stupac, jasno je opet imamo donjetrokutastu matricu, dakle determinanta je umnozak elemenata na dijagonali 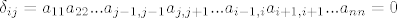 jer je npr. jer je npr. 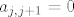
za ovu drugu tvrdnju znamo da je 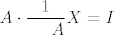 , lako se vidi da kod mnozenja (donje)trokutastih matrica na dijagonalnim mjestima imamo bas umnozak koeficijenata na istim dijagonalnim mjestima od polaznih matrica.... ja i objasnjavanje... od tud slijedi tvrdnja, jer , lako se vidi da kod mnozenja (donje)trokutastih matrica na dijagonalnim mjestima imamo bas umnozak koeficijenata na istim dijagonalnim mjestima od polaznih matrica.... ja i objasnjavanje... od tud slijedi tvrdnja, jer 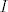 ima na svim dijagonalnim mjestima ima na svim dijagonalnim mjestima  , pa ako na nekom ima , pa ako na nekom ima  mora imat i inverz mora imat i inverz
_________________
Mario Berljafa
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
 Postano: 22:59 pon, 23. 2. 2009 Naslov: Postano: 22:59 pon, 23. 2. 2009 Naslov: |
    |
|
|
[quote="mycky1111"]prof je danas rekao da je u ponedjeljak vjerojatno zadnji termin pismenog dijela usmenog, i da ce mozda bit malo kasnije nego inace jer pocinje nastava.
i opet ce se pisat pismeni dio, ali bez eliminacijskog dijela, vec nesto kratko, vrlo vjerojatno slicno drugom dijelu ovih testova do sada(nesto dokazat, napisat, neki teorijski zadacic)...
i mislim da na to MORAJU izaci i oni s popravnih (jer to vam je zadnja sansa za la1)
ali, pitajte prof... :D[/quote]
Upravo tako, to je posljednja prilika za položiti LA1.
Točan termin u ponedjeljak moram još provjeriti sa satničarem.
Usmeni će biti u utorak i srijedu.
- Nenad Antonić
| mycky1111 (napisa): | prof je danas rekao da je u ponedjeljak vjerojatno zadnji termin pismenog dijela usmenog, i da ce mozda bit malo kasnije nego inace jer pocinje nastava.
i opet ce se pisat pismeni dio, ali bez eliminacijskog dijela, vec nesto kratko, vrlo vjerojatno slicno drugom dijelu ovih testova do sada(nesto dokazat, napisat, neki teorijski zadacic)...
i mislim da na to MORAJU izaci i oni s popravnih (jer to vam je zadnja sansa za la1)
ali, pitajte prof...  |
Upravo tako, to je posljednja prilika za položiti LA1.
Točan termin u ponedjeljak moram još provjeriti sa satničarem.
Usmeni će biti u utorak i srijedu.
- Nenad Antonić
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
|
| [Vrh] |
|
nenad
Moderator

Pridružen/a: 08. 10. 2002. (14:08:30)
Postovi: (355)16
|
 Postano: 20:57 pon, 2. 3. 2009 Naslov: Postano: 20:57 pon, 2. 3. 2009 Naslov: |
    |
|
|
Raspored usmenih ispita
(nadam se u 201; ako ne, onda će obavijest biti na oglasnoj ploči ispred mog ureda):
utorak, 3.3.
14:30 Vedrana Rogić, Sany Vranješ, Maja Trpčić, Amalija Oršolić
15:30 Sandra Nežić, Jelena Mađarević, Tea Poturica, Lidija Škuflić
16:30 Damjan Murković, Josip Matijević
17:00 studenti koji nisu na popisu, a ranije su pisali pismeni dio (*)
srijeda, 4.3.
14:15 Nera Petković, Robert Žgela, Goran Vuković, Tomislav Smetko (popravak testova)
14:30 Dino Pavić, Petra Vukašinović, Marina Volarić
15:30 Marta Topić, Lovro Rožić, Terezija Malović
16:45 Ana Vidaček, Anamarija Pavleković, Ivan Puntarić, Ante Perić
četvrtak, 5.3.
8:30 Anthea Paulić, Dijana Turek, Martina Soldo, Tomislav Matulić
9:30 Marija Pijević, studenti koji nisu na popisu, a ranije su pisali pismeni dio (*)
(*) Ukoliko trebate pisati i popravak testova, dođite u srijedu u 14:15
- Nenad Antonić
Raspored usmenih ispita
(nadam se u 201; ako ne, onda će obavijest biti na oglasnoj ploči ispred mog ureda):
utorak, 3.3.
14:30 Vedrana Rogić, Sany Vranješ, Maja Trpčić, Amalija Oršolić
15:30 Sandra Nežić, Jelena Mađarević, Tea Poturica, Lidija Škuflić
16:30 Damjan Murković, Josip Matijević
17:00 studenti koji nisu na popisu, a ranije su pisali pismeni dio (*)
srijeda, 4.3.
14:15 Nera Petković, Robert Žgela, Goran Vuković, Tomislav Smetko (popravak testova)
14:30 Dino Pavić, Petra Vukašinović, Marina Volarić
15:30 Marta Topić, Lovro Rožić, Terezija Malović
16:45 Ana Vidaček, Anamarija Pavleković, Ivan Puntarić, Ante Perić
četvrtak, 5.3.
8:30 Anthea Paulić, Dijana Turek, Martina Soldo, Tomislav Matulić
9:30 Marija Pijević, studenti koji nisu na popisu, a ranije su pisali pismeni dio (*)
(*) Ukoliko trebate pisati i popravak testova, dođite u srijedu u 14:15
- Nenad Antonić
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 23:37 pon, 2. 3. 2009 Naslov: Postano: 23:37 pon, 2. 3. 2009 Naslov: |
    |
|
|
[quote="mycky1111"]primjer da unija dva potprostora nije potprostor[/quote]
stavis da je [latex]V=\mathbb{R}^2, L,M\leq V[/latex]
[latex]L=\{ (x,0)\in\mathbb{R}^2 :x\in \mathbb{R} \}, M=\{ (0,x)\in\mathbb{R}^2 :x\in \mathbb{R} \}[/latex]
[latex]l=(1,0), m=(0,1), l+m=(1,1)\notin L\cup M[/latex]
primjer se bazira na tome da uzmes neka dva pravca(ja sam uzeo osi...) unija su ta dva pravca, i njihova linearna ljuska je vektorski prostor, al unija nije jer znamo da za vektorski prostor [latex]V[/latex] nad poljem [latex]\mathbb{F}[/latex] vrijedi [latex]v_1,v_2\in V, \alpha ,\beta \in\mathbb{F}\Rightarrow \alpha v_1 + \beta v_2 \in V[/latex]
a gore imamo [latex] l\in L\Rightarrow l \in L\cup M,m\in M\Rightarrow m \in L\cup M, l+m\notin L\cup M[/latex]
[size=9][color=#999999]Added after 13 minutes:[/color][/size]
[quote="mycky1111"]ako su A, B, A+B regularne, da je i B^(-1) + A^(-1) isto regularna?![/quote]
ako su [latex]A,B[/latex] i [latex]A+B[/latex] regularne tada postoje [latex]A^{-1}[/latex] i [latex]B^{-1}[/latex] i posebno, kao umnozak regularnih matrica, regularna je i matrica [latex]A^{-1}(A+B)B^{-1}=(A^{-1}A+A^{-1}B)B^{-1}=(I+A^{-1}B)B^{-1}=B^{-1}+A^{-1}[/latex]
| mycky1111 (napisa): | | primjer da unija dva potprostora nije potprostor |
stavis da je 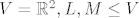
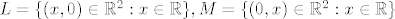
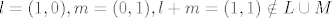
primjer se bazira na tome da uzmes neka dva pravca(ja sam uzeo osi...) unija su ta dva pravca, i njihova linearna ljuska je vektorski prostor, al unija nije jer znamo da za vektorski prostor 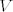 nad poljem nad poljem 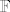 vrijedi vrijedi 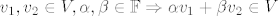
a gore imamo 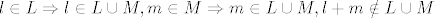
Added after 13 minutes:
| mycky1111 (napisa): | | ako su A, B, A+B regularne, da je i B^(-1) + A^(-1) isto regularna?! |
ako su 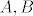 i i 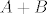 regularne tada postoje regularne tada postoje 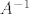 i i 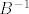 i posebno, kao umnozak regularnih matrica, regularna je i matrica i posebno, kao umnozak regularnih matrica, regularna je i matrica 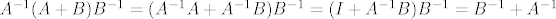
_________________
Mario Berljafa
|
|
| [Vrh] |
|
|













