| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
necka
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (20:09:04)
Postovi: (7)16
|
|
| [Vrh] |
|
necka
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (20:09:04)
Postovi: (7)16
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
 Postano: 17:33 pet, 3. 4. 2009 Naslov: Postano: 17:33 pet, 3. 4. 2009 Naslov: |
    |
|
|
Daj mi objasni kako si uspjela skuziti da je to binomna sl. var, a onda ne znas izracunati ocekivanje :lol:, [size=5]prof. Sarapa bi dobio infarkt![/size]!
[latex]X=\sum_{k=1}^n\chi_{\{X_k=6\}}, \chi_{\{X_k=6\}}\sim \left(\begin{array}{cc}
0 & 1 \\
\frac{5}{6} & \frac{1}{6} \\
\end{array}\right) \Rightarrow X\sim B(n,\frac{1}{6}) [/latex]
U prvom slucaju, nadi [latex]\mathbb{P}(0<X\leq 3)[/latex], u drugom slucaju koristi jedan jako poznati teorem koji ja ovom prilikom necu spomenuti :D , tako da barem nesta solo napravite.
Vidim da ekonomisti rasturaju PMF, taman pred rokove ( ako se ne varam sutra pocinju ! ) :lol:
Edit: Zeznuo sam u ovom prvom, nisam uzeo korjen varijance, to vi sredite, nemam volje to raditi...
Daj mi objasni kako si uspjela skuziti da je to binomna sl. var, a onda ne znas izracunati ocekivanje  , prof. Sarapa bi dobio infarkt!! , prof. Sarapa bi dobio infarkt!!
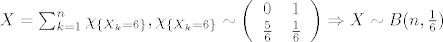
U prvom slucaju, nadi 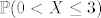 , u drugom slucaju koristi jedan jako poznati teorem koji ja ovom prilikom necu spomenuti , u drugom slucaju koristi jedan jako poznati teorem koji ja ovom prilikom necu spomenuti  , tako da barem nesta solo napravite. , tako da barem nesta solo napravite.
Vidim da ekonomisti rasturaju PMF, taman pred rokove ( ako se ne varam sutra pocinju ! ) 
Edit: Zeznuo sam u ovom prvom, nisam uzeo korjen varijance, to vi sredite, nemam volje to raditi...
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
|
| [Vrh] |
|
ivica13
Forumaš(ica)

Pridružen/a: 03. 10. 2007. (14:01:02)
Postovi: (102)16
Spol: 
|
|
| [Vrh] |
|
finalni
Forumaš(ica)


Pridružen/a: 04. 08. 2007. (11:48:53)
Postovi: (10D)16
Spol: 
Lokacija: Bloodbuzz Zagreb
|
 Postano: 15:40 ned, 21. 6. 2009 Naslov: Postano: 15:40 ned, 21. 6. 2009 Naslov: |
    |
|
|
možda ovako (to je ak kutije razlikujemo a lopte ne).. Ukupno rasporeda ima [latex]\binom{2n-1}{n}[/latex] (zamisli da stavljaš n-1 pregradu u niz od n lopti, ono prije prve pregrade ide u prvu kutiju, ono između prve i druge pregrade u drugu, itd. zapravo, moraš izabrat n mjesta gdje ćeš stavit lopte u niz od 2n-1 mjesta, a na preostala mjesta moraju ići pregrade).
Rasporede u kojima je točno jedna kutija prazna brojimo ovako: kutiju koja je prazna možemo izabrati na [b]n[/b] načina, a u preostalih n-1 mora bit bar 1 lopta => u jednoj kutiji su 2 lopte, u preostale n-2 po 1. Sad tu jednu u koju ćemo stavit 2 lopte možemo izabrati na [b]n-1[/b] način, pa je ukupno tih rasporeda n*(n-1).
Svi rasporedi jednako su vjerojatni => tražena vjerojatnost je [latex]\frac{n\cdot(n-1)}{\binom{2n-1}{n}}[/latex]
možda ovako (to je ak kutije razlikujemo a lopte ne).. Ukupno rasporeda ima 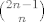 (zamisli da stavljaš n-1 pregradu u niz od n lopti, ono prije prve pregrade ide u prvu kutiju, ono između prve i druge pregrade u drugu, itd. zapravo, moraš izabrat n mjesta gdje ćeš stavit lopte u niz od 2n-1 mjesta, a na preostala mjesta moraju ići pregrade). (zamisli da stavljaš n-1 pregradu u niz od n lopti, ono prije prve pregrade ide u prvu kutiju, ono između prve i druge pregrade u drugu, itd. zapravo, moraš izabrat n mjesta gdje ćeš stavit lopte u niz od 2n-1 mjesta, a na preostala mjesta moraju ići pregrade).
Rasporede u kojima je točno jedna kutija prazna brojimo ovako: kutiju koja je prazna možemo izabrati na n načina, a u preostalih n-1 mora bit bar 1 lopta ⇒ u jednoj kutiji su 2 lopte, u preostale n-2 po 1. Sad tu jednu u koju ćemo stavit 2 lopte možemo izabrati na n-1 način, pa je ukupno tih rasporeda n*(n-1).
Svi rasporedi jednako su vjerojatni ⇒ tražena vjerojatnost je 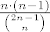
_________________
Nikola Adžaga
Građevinski fakultet, Sveučilište u Zagrebu
|
|
| [Vrh] |
|
|






