| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
branimirb
Forumaš(ica)

Pridružen/a: 03. 09. 2008. (15:39:44)
Postovi: (18)16
Spol: 
|
|
| [Vrh] |
|
Spectre
Forumaš(ica)


Pridružen/a: 02. 10. 2006. (16:58:05)
Postovi: (167)16
Spol: 
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 11:58 uto, 7. 4. 2009 Naslov: Postano: 11:58 uto, 7. 4. 2009 Naslov: |
    |
|
|
Edit: uvukla mi se veća greškica. Originalni post sam umanjio, ispraviti ću kad nađem vremena.
[size=1]Traže se dvije točke (x_1,y(y_1)) i (x_2,y(x_2)) takve da je x_1 \neq x_2 i y'(x_1)=y'(x_2). Kako je y'(x)=4x^3-6x^2-6x+5 tada je
y'(x_1)=y'(x_2) \iff x_1(2x_1^2-3x_1-3)=x_2(2x_2^2-3x_2-3),
a kako mora biti x_1 \neq x_2, tada je
x_1=2x_2^2-3x_2-3\\
x_2=2x_1^2-3x_1-3.
Iz tog sustava dobiti će se jednadžba 4. stupnja koja ima četiri rješenja,
x_1 \in \{-1,2,\frac{1}{2}(2-\sqrt{10}),\frac{1}{2}(2+\sqrt{10})\}
od kojih samo -1 i 2 zadovoljavaju x_1 \neq x_2 te vrijedi da ako je x_1=-1, onda je x_2=2 i ako je x_1=2, onda je x_2=-1 pa možemo uzeti (x_1,x_2)=(-1,2). Sada je pravac koji prolazi točkama (-1,y(1)) i (2,y(2)) traženi pravac.
Trebalo bi još provjeriti da on zbilja je tangenta (ja sam nacrtao u mathematici i poklapa se), tj. da siječe krivulju u samo dvije točke i da oblik krivulje (intervali monotonosti i to sve) ne dozvoljava da ju sječe bilokako već samo kao tangenta.[/size]
Edit: uvukla mi se veća greškica. Originalni post sam umanjio, ispraviti ću kad nađem vremena.
Traže se dvije točke (x_1,y(y_1)) i (x_2,y(x_2)) takve da je x_1 \neq x_2 i y'(x_1)=y'(x_2). Kako je y'(x)=4x^3-6x^2-6x+5 tada je
y'(x_1)=y'(x_2) \iff x_1(2x_1^2-3x_1-3)=x_2(2x_2^2-3x_2-3),
a kako mora biti x_1 \neq x_2, tada je
x_1=2x_2^2-3x_2-3\\
x_2=2x_1^2-3x_1-3.
Iz tog sustava dobiti će se jednadžba 4. stupnja koja ima četiri rješenja,
x_1 \in \{-1,2,\frac{1}{2}(2-\sqrt{10}),\frac{1}{2}(2+\sqrt{10})\}
od kojih samo -1 i 2 zadovoljavaju x_1 \neq x_2 te vrijedi da ako je x_1=-1, onda je x_2=2 i ako je x_1=2, onda je x_2=-1 pa možemo uzeti (x_1,x_2)=(-1,2). Sada je pravac koji prolazi točkama (-1,y(1)) i (2,y(2)) traženi pravac.
Trebalo bi još provjeriti da on zbilja je tangenta (ja sam nacrtao u mathematici i poklapa se), tj. da siječe krivulju u samo dvije točke i da oblik krivulje (intervali monotonosti i to sve) ne dozvoljava da ju sječe bilokako već samo kao tangenta.
_________________
The Dude Abides
Zadnja promjena: goranm; 15:34 uto, 7. 4. 2009; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
 Postano: 19:43 uto, 21. 4. 2009 Naslov: Postano: 19:43 uto, 21. 4. 2009 Naslov: |
    |
|
|
[quote="goranm"]Edit: uvukla mi se veća greškica. Originalni post sam umanjio, ispraviti ću kad nađem vremena.
[size=1]Traže se dvije točke (x_1,y(y_1)) i (x_2,y(x_2)) takve da je x_1 \neq x_2 i y'(x_1)=y'(x_2). Kako je y'(x)=4x^3-6x^2-6x+5 tada je
y'(x_1)=y'(x_2) \iff x_1(2x_1^2-3x_1-3)=x_2(2x_2^2-3x_2-3),
a kako mora biti x_1 \neq x_2, tada je
x_1=2x_2^2-3x_2-3\\
x_2=2x_1^2-3x_1-3.
Iz tog sustava dobiti će se jednadžba 4. stupnja koja ima četiri rješenja,
x_1 \in \{-1,2,\frac{1}{2}(2-\sqrt{10}),\frac{1}{2}(2+\sqrt{10})\}
od kojih samo -1 i 2 zadovoljavaju x_1 \neq x_2 te vrijedi da ako je x_1=-1, onda je x_2=2 i ako je x_1=2, onda je x_2=-1 pa možemo uzeti (x_1,x_2)=(-1,2). Sada je pravac koji prolazi točkama (-1,y(1)) i (2,y(2)) traženi pravac.
Trebalo bi još provjeriti da on zbilja je tangenta (ja sam nacrtao u mathematici i poklapa se), tj. da siječe krivulju u samo dvije točke i da oblik krivulje (intervali monotonosti i to sve) ne dozvoljava da ju sječe bilokako već samo kao tangenta.[/size][/quote]
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
oups....sori..nisam trebo postat ništa
| goranm (napisa): | Edit: uvukla mi se veća greškica. Originalni post sam umanjio, ispraviti ću kad nađem vremena.
Traže se dvije točke (x_1,y(y_1)) i (x_2,y(x_2)) takve da je x_1 \neq x_2 i y'(x_1)=y'(x_2). Kako je y'(x)=4x^3-6x^2-6x+5 tada je
y'(x_1)=y'(x_2) \iff x_1(2x_1^2-3x_1-3)=x_2(2x_2^2-3x_2-3),
a kako mora biti x_1 \neq x_2, tada je
x_1=2x_2^2-3x_2-3\\
x_2=2x_1^2-3x_1-3.
Iz tog sustava dobiti će se jednadžba 4. stupnja koja ima četiri rješenja,
x_1 \in \{-1,2,\frac{1}{2}(2-\sqrt{10}),\frac{1}{2}(2+\sqrt{10})\}
od kojih samo -1 i 2 zadovoljavaju x_1 \neq x_2 te vrijedi da ako je x_1=-1, onda je x_2=2 i ako je x_1=2, onda je x_2=-1 pa možemo uzeti (x_1,x_2)=(-1,2). Sada je pravac koji prolazi točkama (-1,y(1)) i (2,y(2)) traženi pravac.
Trebalo bi još provjeriti da on zbilja je tangenta (ja sam nacrtao u mathematici i poklapa se), tj. da siječe krivulju u samo dvije točke i da oblik krivulje (intervali monotonosti i to sve) ne dozvoljava da ju sječe bilokako već samo kao tangenta. |
Added after 2 minutes:
oups....sori..nisam trebo postat ništa
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 1:25 sri, 22. 4. 2009 Naslov: Postano: 1:25 sri, 22. 4. 2009 Naslov: |
    |
|
|
Ok, novi pokušaj. :) Pretpostavimo da postoji tangenta [latex]t(x)=kx+l[/latex] koja siječe zadani polinom u točno dvije točke [latex](x_1,t(x_1))[/latex] i [latex](x_2, t(x_2))[/latex]. Tada je [latex]y(x)-t(x)[/latex] polinom četvrtog stupnja sa dvije dvostruke nultočke [latex]x_1[/latex] i [latex]x_2[/latex] pa je oblika
[latex]a(x-x_1)^2(x-x_2)^2 = \\
a x^4 + a x^3 (-2 x_1 - 2 x_2) +
a x^2 (x_1^2 + 4 x_1 x_2 + x_2^2) + a x (-2 x_1^2 x_2 - 2 x_1 x_2^2)+ a x_1^2 x_2^2.[/latex]
Koeficijenti uz [latex]x^2, x^3[/latex] i [latex]x^4[/latex] su isti i kod [latex]y(x)[/latex] i kod [latex]y(x)-t(x)[/latex] pa imamo
[latex]a=1, x_1+x_2=1, x_1^2+4x_1x_2+x_2^2=-3.[/latex]
Iz toga slijedi da je [latex](x_1,x_2)=(-1,2)[/latex] ili [latex](x_1,x_2)=(2,-1)[/latex] pa možemo uzeti [latex](x_1,x_2)=(-1,2)[/latex]. Iz toga slijedi da je tražena tangenta dana sa [latex]t(x)=x+2[/latex].
Ok, novi pokušaj.  Pretpostavimo da postoji tangenta Pretpostavimo da postoji tangenta 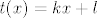 koja siječe zadani polinom u točno dvije točke koja siječe zadani polinom u točno dvije točke 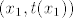 i i 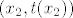 . Tada je . Tada je  polinom četvrtog stupnja sa dvije dvostruke nultočke polinom četvrtog stupnja sa dvije dvostruke nultočke 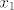 i i 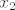 pa je oblika pa je oblika
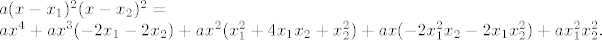
Koeficijenti uz 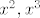 i i 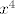 su isti i kod su isti i kod 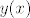 i kod i kod  pa imamo pa imamo
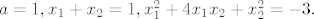
Iz toga slijedi da je 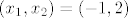 ili ili 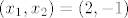 pa možemo uzeti pa možemo uzeti 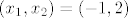 . Iz toga slijedi da je tražena tangenta dana sa . Iz toga slijedi da je tražena tangenta dana sa 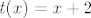 . .
_________________
The Dude Abides
|
|
| [Vrh] |
|
prove22
Forumaš(ica)

Pridružen/a: 11. 02. 2009. (18:57:32)
Postovi: (2F)16
|
|
| [Vrh] |
|
|











