| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
moki
Forumaš(ica)
Pridružen/a: 07. 04. 2009. (14:10:47)
Postovi: (4)16
|
|
| [Vrh] |
|
ma
Forumaš(ica)
Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
moki
Forumaš(ica)
Pridružen/a: 07. 04. 2009. (14:10:47)
Postovi: (4)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
 Postano: 16:30 uto, 7. 4. 2009 Naslov: |
    |
|
|
Ma ne treba ti to sve... napiso sam ti gore kak još možeš napisat opći član, dakle
[latex]x_n = \frac{n}{n+1} = 1 - \frac{1}{n+1}[/latex]
i sad kad tu lupiš limes imaš
[latex]\lim_{n \to \infty}{x_n} = \lim_{n \to \infty}{( 1 - \frac{1}{n+1} )} = 1 - \lim_{n \to \infty}{(\frac{1}{n+1})}=1-0=1[/latex]
ako baš želiš sa e-om, onda ti je kriv zadnji korak, jer je
[latex]e^{ \lim_{n \to \infty}{(\frac{-1}{n+1})}} = e^0 =1[/latex]
inače, primjeti da imaš rastuć niz, ograničen odozgo sa 1, pa limes nikako ne može bit neka beskonačnost (u +besk ne može jer nejde preko 1, a u -besk ne može jer raste od 0 ili 1/2 ovisno dal n ide od 0 ili 1)
Ma ne treba ti to sve... napiso sam ti gore kak još možeš napisat opći član, dakle
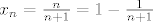
i sad kad tu lupiš limes imaš
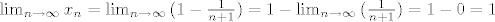
ako baš želiš sa e-om, onda ti je kriv zadnji korak, jer je
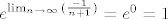
inače, primjeti da imaš rastuć niz, ograničen odozgo sa 1, pa limes nikako ne može bit neka beskonačnost (u +besk ne može jer nejde preko 1, a u -besk ne može jer raste od 0 ili 1/2 ovisno dal n ide od 0 ili 1)
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy 
Zadnja promjena: Luuka; 16:34 uto, 7. 4. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
moki
Forumaš(ica)
Pridružen/a: 07. 04. 2009. (14:10:47)
Postovi: (4)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
moki
Forumaš(ica)
Pridružen/a: 07. 04. 2009. (14:10:47)
Postovi: (4)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
| Postano: 17:15 uto, 7. 4. 2009 Naslov: |
|
|
|
[quote="moki"]Da li je niz [latex]X_n = \frac{n}{n+1}[/latex] konvergentan? Da li je Cauchyjev? Obrazlozite!
dakle ja sam ovime preko limesa dokazao da je konvergentan ne? jer nemoze bit konvergentan bez limesa kolko sam skuzio taj dio . . . ali nekuzim koja je onda razlika izmedu njega i Cauchyevog (jer kolko sam ja shvatio Cauchyev je onaj koji je skuplja oko jednog broja a to je i definicija limesa)[/quote]
Dakle, niz jest konvergentan, a to je zato jer je monoton i ograničen (monoton -> u ovom slučaju rastuć i ograničen->odozgo sa 1).
Pošto je konvergentan, limes postoji i iznosi 1.
Taj niz je i Cauchyev jer se nalazimo u potpunom prostoru (R) u kojem je svaki konvergentan ujedno i Cauchyev.
A razlika između konvergentog i Cauchyevog je da kod konv se svi nakupljaju oko 1 limesa, ali nema nikakvog uvjeta na odnos između članova niza. Cauchyev je onaj kojem su od nekog nadalje članovi po volji blizu (međusobno, a ne limesu, jer C niz ni ne mora konvergirati)
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
evo jedan primjer niza koji je C niz, ali nije konvergentan.
Promatramo niz (u Q - racionalnim brojevima)
[latex]x_n= (1+\frac{1}{n})^n[/latex]
Taj niz jest C niz u Q, ali nije konvergentan (pazi, nad Q smo, a limes ovoga je e, koji nije iz Q, a limes mora biti iz istog skupa u kojem je niz).
| moki (napisa): | Da li je niz 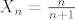 konvergentan? Da li je Cauchyjev? Obrazlozite!
dakle ja sam ovime preko limesa dokazao da je konvergentan ne? jer nemoze bit konvergentan bez limesa kolko sam skuzio taj dio . . . ali nekuzim koja je onda razlika izmedu njega i Cauchyevog (jer kolko sam ja shvatio Cauchyev je onaj koji je skuplja oko jednog broja a to je i definicija limesa) |
Dakle, niz jest konvergentan, a to je zato jer je monoton i ograničen (monoton → u ovom slučaju rastuć i ograničen→odozgo sa 1).
Pošto je konvergentan, limes postoji i iznosi 1.
Taj niz je i Cauchyev jer se nalazimo u potpunom prostoru (R) u kojem je svaki konvergentan ujedno i Cauchyev.
A razlika između konvergentog i Cauchyevog je da kod konv se svi nakupljaju oko 1 limesa, ali nema nikakvog uvjeta na odnos između članova niza. Cauchyev je onaj kojem su od nekog nadalje članovi po volji blizu (međusobno, a ne limesu, jer C niz ni ne mora konvergirati)
Added after 4 minutes:
evo jedan primjer niza koji je C niz, ali nije konvergentan.
Promatramo niz (u Q - racionalnim brojevima)
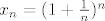
Taj niz jest C niz u Q, ali nije konvergentan (pazi, nad Q smo, a limes ovoga je e, koji nije iz Q, a limes mora biti iz istog skupa u kojem je niz).
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy |
|
| [Vrh] |
|
goranm
Forumaš(ica)
Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
| Postano: 17:16 uto, 7. 4. 2009 Naslov: |
|
|
|
Nisu ti iste definicije Cauchyevog niza i limesa niza. U nekim prostorima Cauchyev niz ne mora imati limes. Točka (broj) x je limes nekog niza ako nakon tamo nekog n-tog člana tog niza su svi članovi jako blizu točki x, dok je niz Cauchyev ako su nakon nekog n-tog člana niza svaka dva člana međusobno jako blizu.
Time što je tvoj niz Xn konvergentan si pokazao da je on i Cauchyev u [u]potpunom[/u] metričkom prostoru, tj. u [latex]\mathbb{R}[/latex].
No tvoje pitanje je bilo da li konvergira i da li je Cauchyev na [latex]\left[0,1\right\rangle[/latex]. Zatvoreni potprostori potpunog metričkog prostora su također potpuni, no [latex]\left[0,1\right\rangle[/latex] nije zatvoren potprostor od [latex]\mathbb{R}[/latex] tako da se ne možeš lako izvuć preko tvrdnje konvergentan=cauchyev, već moraš preko definicija provjeriti što je ili nije. :)
Nisu ti iste definicije Cauchyevog niza i limesa niza. U nekim prostorima Cauchyev niz ne mora imati limes. Točka (broj) x je limes nekog niza ako nakon tamo nekog n-tog člana tog niza su svi članovi jako blizu točki x, dok je niz Cauchyev ako su nakon nekog n-tog člana niza svaka dva člana međusobno jako blizu.
Time što je tvoj niz Xn konvergentan si pokazao da je on i Cauchyev u potpunom metričkom prostoru, tj. u  .
No tvoje pitanje je bilo da li konvergira i da li je Cauchyev na 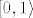 . Zatvoreni potprostori potpunog metričkog prostora su također potpuni, no 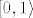nije zatvoren potprostor od tako da se ne možeš lako izvuć preko tvrdnje konvergentan=cauchyev, već moraš preko definicija provjeriti što je ili nije. 
_________________
The Dude Abides
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol:
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
|
hvala
