| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
 Postano: 18:57 sri, 15. 4. 2009 Naslov: Prva zadaća Postano: 18:57 sri, 15. 4. 2009 Naslov: Prva zadaća |
    |
|
|
Hello, hello!
Imam problemčić s jednim obratom, a nitko za to nije pitao pa će mi valjda netko znati pomoći :)
Naime... u drugom zadatku (u obratu, prvi smijer je lagan) treba dokazati da, ako je sp komponirano s sq jednako sq komponirano s sp, onda su p i q okomiti. Fali mi ideja koje se ne bi oslanjale izravno na sliku :? sve što je meni palo na pamet se da samo nacrtati, ništa se ne da raspisati preko definicije simetrije :?
Hello, hello!
Imam problemčić s jednim obratom, a nitko za to nije pitao pa će mi valjda netko znati pomoći 
Naime... u drugom zadatku (u obratu, prvi smijer je lagan) treba dokazati da, ako je sp komponirano s sq jednako sq komponirano s sp, onda su p i q okomiti. Fali mi ideja koje se ne bi oslanjale izravno na sliku  sve što je meni palo na pamet se da samo nacrtati, ništa se ne da raspisati preko definicije simetrije sve što je meni palo na pamet se da samo nacrtati, ništa se ne da raspisati preko definicije simetrije 
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 19:51 sri, 15. 4. 2009 Naslov: Postano: 19:51 sri, 15. 4. 2009 Naslov: |
    |
|
|
Tm kaže.....
a) Ako su [latex]$a$[/latex] i [latex]$b$[/latex] okomiti pravci s sjecištem u [latex]$C$[/latex] tada je [latex]$s_a \circ s_b = s_b \circ s_a = s_C$[/latex]
b) [latex]$s_a \circ s_b = s_C, a \ne b \Rightarrow C = a \cap b, a \perp b$[/latex]
Dokaz.....
a) pogledaj koordinatni sustav...uzmi bilo koju tocku (x, y); [latex]$a$[/latex] je os [latex]$x$[/latex], a [latex]$b$[/latex] je os [latex]$y$[/latex]
[latex]$s_b (x, y) = (-x, y) \\ s_a (x, y) = (x, -y) \\ s_C (x, y) = (-x, -y) \\ (s_a \circ s_b)(x, y) = s_a(s_b(x, y)) = s_a(-x, y) = (-x, -y) = s_C (x, y)$[/latex]
s obzirom da to vrijedi za svaku tocku (x, y) zakljucujemo da je [latex]$s_a \circ s_b = s_C$[/latex]
analogno se dokazuje za [latex]$s_b \circ s_a$[/latex]
b) buduci da imamo kompoziciju, sjecište [latex]$a \cap b$[/latex] (ako postoji) je jedina fiksna tocka od [latex]$s_a \circ s_b[/latex] (po tm koji kaze da ako je [latex]$a \ne b$[/latex], tada je tocka [latex]$a \cap b$[/latex] jedina fixna tocka izometrije [latex]$s_b \circ s_a$[/latex])
s obzirom da je [latex]$C = a \cap b$[/latex], onda je jedina fixna tocka izometrije [latex]$s_C$[/latex] upravo tocka [latex]$C = a \cap b$[/latex]
----
buduci se ta preslikavanja podudaraju, pogledaj u tocki [latex]$C$[/latex] okomicu na [latex]$a$[/latex] i nazovimo je [latex]$c$[/latex]. treba dokazati da je [latex]$c = b$[/latex]
[latex]$s_a \circ s_c = s_C \\ s_a \circ s_b = s_C$[/latex]
izjednacimo....
[latex]$s_a \circ s_c = s_a \circ s_b$[/latex]
mnozimo s lijeva sa [latex]$s_a$[/latex], pa dobijemo identitetu [latex]$s_a \circ s_a = id$[/latex], odakle dobivamo [latex]$s_c = s_b \Rightarrow c = b$[/latex] (ako se osne simetrije podudaraju, onda se i pravci podudaraju)
[latex]$ \Rightarrow a \perp b$[/latex] (pretpostavka ja bila da je [latex]$a \perp c$[/latex], a sada smo dokazali da je [latex]$c = b$[/latex])
to je to....
i savjet vise.....kad postavljas pitanje na forum, onda je lijepo napisati tekst cijelog zadatka (a ne "zadatak broj xy"). znas, mi "starudije" ne znamo koje vi zadatke imate... ;)
Tm kaže.....
a) Ako su  i i  okomiti pravci s sjecištem u okomiti pravci s sjecištem u  tada je tada je 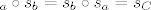
b) 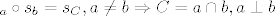
Dokaz.....
a) pogledaj koordinatni sustav...uzmi bilo koju tocku (x, y);  je os je os  , a , a  je os je os 
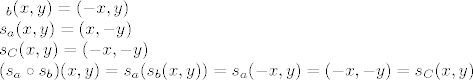
s obzirom da to vrijedi za svaku tocku (x, y) zakljucujemo da je 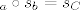
analogno se dokazuje za 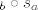
b) buduci da imamo kompoziciju, sjecište 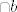 (ako postoji) je jedina fiksna tocka od (ako postoji) je jedina fiksna tocka od 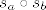 (po tm koji kaze da ako je (po tm koji kaze da ako je 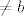 , tada je tocka , tada je tocka 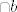 jedina fixna tocka izometrije jedina fixna tocka izometrije 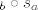 ) )
s obzirom da je 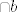 , onda je jedina fixna tocka izometrije , onda je jedina fixna tocka izometrije  upravo tocka upravo tocka 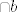
----
buduci se ta preslikavanja podudaraju, pogledaj u tocki  okomicu na okomicu na  i nazovimo je i nazovimo je  . treba dokazati da je . treba dokazati da je 
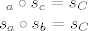
izjednacimo....
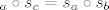
mnozimo s lijeva sa  , pa dobijemo identitetu , pa dobijemo identitetu 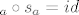 , odakle dobivamo , odakle dobivamo 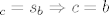 (ako se osne simetrije podudaraju, onda se i pravci podudaraju) (ako se osne simetrije podudaraju, onda se i pravci podudaraju)
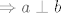 (pretpostavka ja bila da je (pretpostavka ja bila da je  , a sada smo dokazali da je , a sada smo dokazali da je  ) )
to je to....
i savjet vise.....kad postavljas pitanje na forum, onda je lijepo napisati tekst cijelog zadatka (a ne "zadatak broj xy"). znas, mi "starudije" ne znamo koje vi zadatke imate... 
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
 Postano: 21:53 sri, 15. 4. 2009 Naslov: Postano: 21:53 sri, 15. 4. 2009 Naslov: |
    |
|
|
Tnx, kenny! :)
Za tekst uopce nisam razmisljala da nema na netu, obzirom da analiza i linearna uvijek budu. :lol: U ovom zadatku se ne spominje sjecište, samo simetrije. Možda je malo pojednostavljen. Glasi:
"Neka su p i q dva različita pravca ravnine M. Dokažite da su pravci p i q okomiti ako i samo ako vrijedi da je [latex]$s_p \circ s_q = s_q \circ s_p[/latex]."
Nego, da vidim jesam dobro shvatila, malo mi čudno... :zbunjen: sjecište je jedina fiksna točka za sve simetrije? (meni se tako čini) Kako smo onda preko sjecišta mogli zaključiti da je b = c, kad bi b isto tako mogao biti i bilo koji drugi pravac koji prolazi kroz sjecište, i opet bi isto vrijedilo (da je [latex]$s_a \circ s_c = s_a \circ s_b$[/latex])... ili ne bi? :/
Tnx, kenny! 
Za tekst uopce nisam razmisljala da nema na netu, obzirom da analiza i linearna uvijek budu.  U ovom zadatku se ne spominje sjecište, samo simetrije. Možda je malo pojednostavljen. Glasi: U ovom zadatku se ne spominje sjecište, samo simetrije. Možda je malo pojednostavljen. Glasi:
"Neka su p i q dva različita pravca ravnine M. Dokažite da su pravci p i q okomiti ako i samo ako vrijedi da je 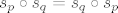 ." ."
Nego, da vidim jesam dobro shvatila, malo mi čudno...  sjecište je jedina fiksna točka za sve simetrije? (meni se tako čini) Kako smo onda preko sjecišta mogli zaključiti da je b = c, kad bi b isto tako mogao biti i bilo koji drugi pravac koji prolazi kroz sjecište, i opet bi isto vrijedilo (da je sjecište je jedina fiksna točka za sve simetrije? (meni se tako čini) Kako smo onda preko sjecišta mogli zaključiti da je b = c, kad bi b isto tako mogao biti i bilo koji drugi pravac koji prolazi kroz sjecište, i opet bi isto vrijedilo (da je 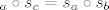 )... ili ne bi? )... ili ne bi? 
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 23:43 sri, 15. 4. 2009 Naslov: Postano: 23:43 sri, 15. 4. 2009 Naslov: |
    |
|
|
kompozicija osnih simetrija (s tim da su a i b okomiti) je komutativna i jednaka je centralnoj simetriji s obzirom na sjeciste. s tim ti pocinje onaj dokaz koji sam pisao pod b).
za ovaj drugi dio.....mi smo birali da da je pravac c okomit na a kako bismo u konacnici dobili da je b = c.
e da.......sjeciste opcenito nije fiksna tocka za simetrije! zapravo, ovo je malo nespretno receno.... koje simetrije? koliko ih ima? (zapravo koliko ima pravaca koji odredjuju te simetrije?) sjeku li se ti pravci u istoj tocki? ako gledas centralnu simetriju - fixan je centar simetrije i svi pravci koji prolaze centrom simetrije (ali tocke tog pravca nisu fiksne - samo je jedna fiksna). sto se tice osne simetrije - fixan je pravac - os simetrije i svaki pravac koji je okomit na os simetrije (ali tocke tih pravaca nisu fiksne - fiksna je samo ona koja je sjeciste osi simetrije i pravca okomitom na os simetrije).
evo ti jedan bonus zadatak - koje preslikavanje dobijemo kada su pravci a i b paralelni, a sto kada se sijeku (ali nisu okomiti)? ne moras nista izvoditi, samo probaj nacrtati i zakljuci..... (opcenito je centralna simetrija zapravo poseban slucaj ovog drugog preslikavanja koje te pitam) --> btw, to je sve osnovnoskolsko gradivo, ali se sada razmatraju u sirem kontekstu
evo jos jedno - jesu li simetrije opcenito komutativne?
kompozicija osnih simetrija (s tim da su a i b okomiti) je komutativna i jednaka je centralnoj simetriji s obzirom na sjeciste. s tim ti pocinje onaj dokaz koji sam pisao pod b).
za ovaj drugi dio.....mi smo birali da da je pravac c okomit na a kako bismo u konacnici dobili da je b = c.
e da.......sjeciste opcenito nije fiksna tocka za simetrije! zapravo, ovo je malo nespretno receno.... koje simetrije? koliko ih ima? (zapravo koliko ima pravaca koji odredjuju te simetrije?) sjeku li se ti pravci u istoj tocki? ako gledas centralnu simetriju - fixan je centar simetrije i svi pravci koji prolaze centrom simetrije (ali tocke tog pravca nisu fiksne - samo je jedna fiksna). sto se tice osne simetrije - fixan je pravac - os simetrije i svaki pravac koji je okomit na os simetrije (ali tocke tih pravaca nisu fiksne - fiksna je samo ona koja je sjeciste osi simetrije i pravca okomitom na os simetrije).
evo ti jedan bonus zadatak - koje preslikavanje dobijemo kada su pravci a i b paralelni, a sto kada se sijeku (ali nisu okomiti)? ne moras nista izvoditi, samo probaj nacrtati i zakljuci..... (opcenito je centralna simetrija zapravo poseban slucaj ovog drugog preslikavanja koje te pitam) --> btw, to je sve osnovnoskolsko gradivo, ali se sada razmatraju u sirem kontekstu
evo jos jedno - jesu li simetrije opcenito komutativne?
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
 Postano: 19:10 čet, 16. 4. 2009 Naslov: Postano: 19:10 čet, 16. 4. 2009 Naslov: |
    |
|
|
pa ne. kompozicija osnih simetrija je centralna simetrija je samo onda kada su osi simetrije okomiti pravci. kada su osi simetrije paralelni pravci, onda je kompozicija osnih simetrija translacija. kada su osi simetrije pravci koji se sijeku u točki R, a ne sijeku se pod pravim kutem, onda je kompozicija tih osnih simetrija rotacija oko tocke R. (centralna simetrija je poseban slucaj rotacije oko sjecista za kut 180°)
a inace, kompozicija simetrija nije komutativna, pa i o tome moras voditi racuna...
pa ne. kompozicija osnih simetrija je centralna simetrija je samo onda kada su osi simetrije okomiti pravci. kada su osi simetrije paralelni pravci, onda je kompozicija osnih simetrija translacija. kada su osi simetrije pravci koji se sijeku u točki R, a ne sijeku se pod pravim kutem, onda je kompozicija tih osnih simetrija rotacija oko tocke R. (centralna simetrija je poseban slucaj rotacije oko sjecista za kut 180°)
a inace, kompozicija simetrija nije komutativna, pa i o tome moras voditi racuna...
_________________
Dvije stvari su beskonacne: svemir i ljudska glupost. Za ono prvo nisam siguran.
by A.Einstein
|
|
| [Vrh] |
|
Tindariel
Forumaš(ica)

Pridružen/a: 03. 12. 2008. (00:49:03)
Postovi: (71)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
|












