| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mesic
Forumaš(ica)

Pridružen/a: 01. 07. 2003. (20:16:56)
Postovi: (35)16
Spol: 
Lokacija: /dev/(m)ucenje
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
|
| [Vrh] |
|
Iki
Forumaš(ica)


Pridružen/a: 22. 08. 2003. (22:43:04)
Postovi: (AA)16
Spol: 
Lokacija: Drzim se susedovog plota
|
 Postano: 14:33 uto, 9. 12. 2008 Naslov: Postano: 14:33 uto, 9. 12. 2008 Naslov: |
    |
|
|
Trebala bi mi mala pomoć oko [url=http://web.math.hr/nastava/alg/pismeni/alg080908]ovog roka[/url], pa ako ima koja dobra duša da mi na brzinu odgovori.
4. zadatak - a) dio mi je jasan, i dobio sam da je generator <2>, ali kako postavite b) tj, kako ispitati da li on je ili nije maksimalan. Intuicija mi govori da neće biti maksimalan, ali ne znam kako to pokazati
5. zadatak - Je li dovoljno napisati da <2x,3> nije maksimalan ideal jer se vidi da je [latex]2x=3\frac{2x}{3}[/latex], tj. Euklidov algoritam nam ne daje ništa?
Trebala bi mi mala pomoć oko ovog roka, pa ako ima koja dobra duša da mi na brzinu odgovori.
4. zadatak - a) dio mi je jasan, i dobio sam da je generator <2>, ali kako postavite b) tj, kako ispitati da li on je ili nije maksimalan. Intuicija mi govori da neće biti maksimalan, ali ne znam kako to pokazati
5. zadatak - Je li dovoljno napisati da <2x,3> nije maksimalan ideal jer se vidi da je 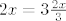 , tj. Euklidov algoritam nam ne daje ništa? , tj. Euklidov algoritam nam ne daje ništa?
_________________
Idu dva vektora ulicom jedan padne i skalarni produkt je nula.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
mischa
Forumaš(ica)

Pridružen/a: 15. 09. 2007. (17:52:41)
Postovi: (D8)16
Spol: 
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 20:46 čet, 16. 4. 2009 Naslov: Postano: 20:46 čet, 16. 4. 2009 Naslov: |
    |
|
|
[quote="mischa"]nikako ne mogu rijesiti 3. zadatak s proslogodisnjeg kolokvija pa bih zamolila za pomoc ili uputu:
da li je {f elem S_5 : f(3)=3} podgrupa od S_5, dokazite? da li postoje podrupe reda 4, 5 i 7 u S_5?[/quote]
Nazovimo S onaj skup za koji se pita da li je podgrupa od S5. Očito
je podskup. Uzmemo neka dva elementa f,g iz S (tj. f(3)=3 i g(3)=3), i
gledamo čemu je jednako fog^-1 (3) //f kružić g na minus prvu od 3//.
Ako je g(3)=3 očito slijedi g^-1(3)=3, pa vrijedi: fog^-1
(3)=f(g^-1(3))=f(3)=3, pa je i fog^-1 opet u S, pa je S podgrupa.
Broj elemenata od S5 je 5!=120. Pa po Langrangeovom teoremu nema
podgrupe reda 7, jer 7 ne dijeli 120. Ali ima reda 4, i 5, samo nadjes
element reda 4 i 5 (cikluse), oni će sami generirati podgrupe reda 4 i
5. Npr: a:=(1234), b=(12345). Sad je (a) podgrupa pd S5 reda 4, a (b)
podgrupa reda 5.
p.s. sorry neda mi se tex-irati, ako ima nejasnoca javi.
| mischa (napisa): | nikako ne mogu rijesiti 3. zadatak s proslogodisnjeg kolokvija pa bih zamolila za pomoc ili uputu:
da li je {f elem S_5 : f(3)=3} podgrupa od S_5, dokazite? da li postoje podrupe reda 4, 5 i 7 u S_5? |
Nazovimo S onaj skup za koji se pita da li je podgrupa od S5. Očito
je podskup. Uzmemo neka dva elementa f,g iz S (tj. f(3)=3 i g(3)=3), i
gledamo čemu je jednako fog^-1 (3) //f kružić g na minus prvu od 3//.
Ako je g(3)=3 očito slijedi g^-1(3)=3, pa vrijedi: fog^-1
(3)=f(g^-1(3))=f(3)=3, pa je i fog^-1 opet u S, pa je S podgrupa.
Broj elemenata od S5 je 5!=120. Pa po Langrangeovom teoremu nema
podgrupe reda 7, jer 7 ne dijeli 120. Ali ima reda 4, i 5, samo nadjes
element reda 4 i 5 (cikluse), oni će sami generirati podgrupe reda 4 i
5. Npr: a:=(1234), b=(12345). Sad je (a) podgrupa pd S5 reda 4, a (b)
podgrupa reda 5.
p.s. sorry neda mi se tex-irati, ako ima nejasnoca javi.
|
|
| [Vrh] |
|
mischa
Forumaš(ica)

Pridružen/a: 15. 09. 2007. (17:52:41)
Postovi: (D8)16
Spol: 
|
|
| [Vrh] |
|
mary
Gost
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 13:49 sub, 18. 4. 2009 Naslov: Postano: 13:49 sub, 18. 4. 2009 Naslov: |
    |
|
|
[quote="mary"]molim pomoc oko 1.zadatka i z 1.kolokvija 2008.god,gdje se trazi red elementa f(i,0)(i,o je indeks dolje)
hvala unaprijed ako ko zna[/quote]
[latex]f_{i,0}(x)=ix+0=ix[/latex], jeli to identiteta (neutralni element u grupi s operacijom komponiranja)? - Nije.
[latex]f_{i,0}^{2}(x)= (f_{i,0} \circ f_{i,0})(x) = f_ {i,0}(f_{i,0}(x)) = f_{i,0}(ix) =i(ix)=i^{2}x=-x[/latex], nije identiteta.
[latex]f^{3}_{i,0}(x)= \ ... \ =-ix[/latex], nije identiteta.
[latex]f^{4}_{i,0}(x)= \ ... \ =x \ \forall x \in \mathbb{C} \ \Rightarrow \ f^{4}_{i,0}=id[/latex]. Dakle, [latex]n=4[/latex] je najmanji prirodan broj td [latex]f^{n}_{i,0}=id[/latex], pa je red elementa [latex]f_{i,0}[/latex] u danoj grupi jednak [latex]4[/latex].
| mary (napisa): | molim pomoc oko 1.zadatka i z 1.kolokvija 2008.god,gdje se trazi red elementa f(i,0)(i,o je indeks dolje)
hvala unaprijed ako ko zna |
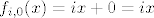 , jeli to identiteta (neutralni element u grupi s operacijom komponiranja)? - Nije. , jeli to identiteta (neutralni element u grupi s operacijom komponiranja)? - Nije.
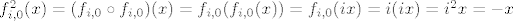 , nije identiteta. , nije identiteta.
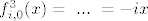 , nije identiteta. , nije identiteta.
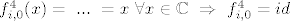 . Dakle, . Dakle, 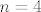 je najmanji prirodan broj td je najmanji prirodan broj td 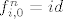 , pa je red elementa , pa je red elementa 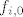 u danoj grupi jednak u danoj grupi jednak 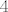 . .
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
|
| [Vrh] |
|
mary
Gost
|
|
| [Vrh] |
|
helpme
Gost
|
|
| [Vrh] |
|
mari
Gost
|
|
| [Vrh] |
|
mari
Gost
|
|
| [Vrh] |
|
Masiela
Forumaš(ica)


Pridružen/a: 11. 09. 2007. (22:28:01)
Postovi: (338)16
Spol: 
Lokacija: Među bananama
|
 Postano: 12:11 ned, 19. 4. 2009 Naslov: Postano: 12:11 ned, 19. 4. 2009 Naslov: |
    |
|
|
[quote="mary"]Napisao si gore: Ako je g(3)=3 očito slijedi g^-1(3)=3,zasto to slijedi?????[/quote]
Ako pričaš o permutacijama, onda zato što je permutacija.
Ako 3 ide u 3, onda kad gledamo inverz 3 ode/se `vrati` u 3.
[size=9][color=#999999]Added after 19 minutes:[/color][/size]
[quote="mari"]Vidim da je n=4p+2=2(2p+1), a ovo u zagradi je prosto pa su 2 i 2p+1 relativno prosti, pa je Z_n izomorfno sa Z_2 x Z_(2p+1)? A to je ciklicka grupa.
Izomorfizmi na ciklickoj su odredjeni djelovanjem na generatoru, ali sto je generator ove grupe?
Ne snalazim se, upomoc. :oops:[/quote]
Ja bi išla sa (1,1) :rofl:
Smišno mi je jer bi ja išla s tim i da mi se reče da ne mogu :D
Je l` bi to bilo dobro?
Mislim... 1 će bit generator u svakoj toj Z nešto, koliko (ni)san skužila.
EDIT: Aha... tebi trebaju generatori od Aut... :evil:
EDIT opet: A... Ako su u Aut(Z nešto) generatori s indeksima relativno prostima s tim nešto, dakle, indeksi su generatori od Z nešto, onda bi tu indeksi mogli bit generatori od Z_...xZ...
Ne znan... Ja bi da mi neko lijepo objasni priču oko generatora automorfizama :roll:
| mary (napisa): | | Napisao si gore: Ako je g(3)=3 očito slijedi g^-1(3)=3,zasto to slijedi????? |
Ako pričaš o permutacijama, onda zato što je permutacija.
Ako 3 ide u 3, onda kad gledamo inverz 3 ode/se `vrati` u 3.
Added after 19 minutes:
| mari (napisa): | Vidim da je n=4p+2=2(2p+1), a ovo u zagradi je prosto pa su 2 i 2p+1 relativno prosti, pa je Z_n izomorfno sa Z_2 x Z_(2p+1)? A to je ciklicka grupa.
Izomorfizmi na ciklickoj su odredjeni djelovanjem na generatoru, ali sto je generator ove grupe?
Ne snalazim se, upomoc.  |
Ja bi išla sa (1,1) 
Smišno mi je jer bi ja išla s tim i da mi se reče da ne mogu 
Je l` bi to bilo dobro?
Mislim... 1 će bit generator u svakoj toj Z nešto, koliko (ni)san skužila.
EDIT: Aha... tebi trebaju generatori od Aut... 
EDIT opet: A... Ako su u Aut(Z nešto) generatori s indeksima relativno prostima s tim nešto, dakle, indeksi su generatori od Z nešto, onda bi tu indeksi mogli bit generatori od Z_...xZ...
Ne znan... Ja bi da mi neko lijepo objasni priču oko generatora automorfizama 
_________________ mladac: e.k.s. je možda 8%, moje znanje ni toliko  |
|
| [Vrh] |
|
mischa
Forumaš(ica)

Pridružen/a: 15. 09. 2007. (17:52:41)
Postovi: (D8)16
Spol: 
|
|
| [Vrh] |
|
|














