| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tomitza
Forumaš(ica)
Pridružen/a: 28. 11. 2008. (19:50:48)
Postovi: (58)16
|
|
| [Vrh] |
|
Gino
Forumaš(ica)
Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 17:33 ned, 19. 4. 2009 Naslov: Re: geometrijska kratnost |
    |
|
|
[quote="tomitza"]ovako, na koji nacin doci do one dijagonalne matrice, u kojoj su na dijagonali svojstvene vrijednosti... pitam zbog nalazenja geom. kratnosti svojs. vrij.... jel ju lakse racunati, ili traziti preko dijag. matr.?[/quote]
operator se moze dijagonalizirati ako i samo ako su algebarska i geometrijska kratnost svake svojstvene vrijednosti jednake
kad nades svojstvene vrijednosti, nades bazu za svojstven potprostor pridruzen toj svojstvenoj vrijednosti, i to za svaku svojstvenu vrijednost
ako je dakle dimenzija svojstvenog potprostora pridruzene mu svojstvene vrijednosti jednaka algebarskoj kratnosti te svojstavene vrijednosti, i ako to vrijedi za sve svojstvene vrijednosti, onda se operator moze dijagonalizirati, a baza u kojoj to uspijeva je upravo unija baza svojstvenih potprostora svih svojstvenih vrijednosti
| tomitza (napisa): | | ovako, na koji nacin doci do one dijagonalne matrice, u kojoj su na dijagonali svojstvene vrijednosti... pitam zbog nalazenja geom. kratnosti svojs. vrij.... jel ju lakse racunati, ili traziti preko dijag. matr.? |
operator se moze dijagonalizirati ako i samo ako su algebarska i geometrijska kratnost svake svojstvene vrijednosti jednake
kad nades svojstvene vrijednosti, nades bazu za svojstven potprostor pridruzen toj svojstvenoj vrijednosti, i to za svaku svojstvenu vrijednost
ako je dakle dimenzija svojstvenog potprostora pridruzene mu svojstvene vrijednosti jednaka algebarskoj kratnosti te svojstavene vrijednosti, i ako to vrijedi za sve svojstvene vrijednosti, onda se operator moze dijagonalizirati, a baza u kojoj to uspijeva je upravo unija baza svojstvenih potprostora svih svojstvenih vrijednosti
_________________
Mario Berljafa
|
|
| [Vrh] |
|
bimar
Forumaš(ica)
Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)
Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
| Postano: 19:09 ned, 19. 4. 2009 Naslov: Re: geometrijska kratnost |
|
|
|
[quote="tomitza"]ovako, na koji nacin doci do one dijagonalne matrice, u kojoj su na dijagonali svojstvene vrijednosti... pitam zbog nalazenja geom. kratnosti svojs. vrij.... jel ju lakse racunati, ili traziti preko dijag. matr.?[/quote]
Većina matrica ni nema dijagonalni oblik ;)
One koje sigurno imaju su matrice NORMALNIH operatora za koje vrijedi [latex]A^* A = A A^*[/latex] (to su recimo simetrične, tj hermitske u komplexnom slučaju)
Kako doć do D i P?
U D idu svojstvene vrijednosti, a u P idu pripadni svojstveni vektori u stupce (ili retke, nisam 100% siguran). Naći sv vektore znaš, i primjećuješ da će taj prikaz postojat samo ako je geom kratnost pojedine sv vrijednosti=alg kratnosti jer ćeš onda moć za svako pojavljivanje od lambda stavit 1 sv vektor u P.
Inače, sve postane ljepše nakon kaj se na Vektorskim prostorima obradi Jordanova forma ;)
| tomitza (napisa): | | ovako, na koji nacin doci do one dijagonalne matrice, u kojoj su na dijagonali svojstvene vrijednosti... pitam zbog nalazenja geom. kratnosti svojs. vrij.... jel ju lakse racunati, ili traziti preko dijag. matr.? |
Većina matrica ni nema dijagonalni oblik 
One koje sigurno imaju su matrice NORMALNIH operatora za koje vrijedi 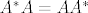 (to su recimo simetrične, tj hermitske u komplexnom slučaju)
Kako doć do D i P?
U D idu svojstvene vrijednosti, a u P idu pripadni svojstveni vektori u stupce (ili retke, nisam 100% siguran). Naći sv vektore znaš, i primjećuješ da će taj prikaz postojat samo ako je geom kratnost pojedine sv vrijednosti=alg kratnosti jer ćeš onda moć za svako pojavljivanje od lambda stavit 1 sv vektor u P.
Inače, sve postane ljepše nakon kaj se na Vektorskim prostorima obradi Jordanova forma
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|
