| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 17:48 uto, 21. 4. 2009 Naslov: Postano: 17:48 uto, 21. 4. 2009 Naslov: |
    |
|
|
[quote="Holomorfan"]Jel bi netko molim vas mogao objasniti sto to znaci holomorfna fja? Citam sad predavanja i kaze da je holomorfna ako ima prvu derivaciju,tada ima sve ostale?! Dal sam u krivu, ili? tj. zanima me kako iz C-R uvjeta ili kako uopce provjeriti holomorfnost? npr. 4 zad iz kolokvija? tnx[/quote]
Holomorfna je (na S) ako za svaki z0 iz S postoji okolina na kojoj je derivabilna i derivacija je neprekidna (onda i ima sve dervacije i sve su neprekidne i da se razvit u red potencija, što nije sad bitno). U 4.zad u kol se dobije da je derivabilna samo u jednoj točki, dakle nije holomorfna jer nema okoline...
| Holomorfan (napisa): | | Jel bi netko molim vas mogao objasniti sto to znaci holomorfna fja? Citam sad predavanja i kaze da je holomorfna ako ima prvu derivaciju,tada ima sve ostale?! Dal sam u krivu, ili? tj. zanima me kako iz C-R uvjeta ili kako uopce provjeriti holomorfnost? npr. 4 zad iz kolokvija? tnx |
Holomorfna je (na S) ako za svaki z0 iz S postoji okolina na kojoj je derivabilna i derivacija je neprekidna (onda i ima sve dervacije i sve su neprekidne i da se razvit u red potencija, što nije sad bitno). U 4.zad u kol se dobije da je derivabilna samo u jednoj točki, dakle nije holomorfna jer nema okoline...
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
garbica
Forumaš(ica)


Pridružen/a: 11. 06. 2007. (00:24:08)
Postovi: (D)16
Spol: 
Lokacija: otok sreće...
|
|
| [Vrh] |
|
sun
Forumaš(ica)

Pridružen/a: 07. 04. 2006. (13:57:24)
Postovi: (A8)16
Spol: 
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
anab
Forumaš(ica)

Pridružen/a: 25. 02. 2008. (20:19:16)
Postovi: (4)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:51 uto, 21. 4. 2009 Naslov: Postano: 18:51 uto, 21. 4. 2009 Naslov: |
    |
|
|
[quote="anab"]
2)Integral(zsinzdz) i integral ide po dijelu pravca od tocke z1=0 do z2=1+i[/quote]
f(z)=zsinz ima primitivnu svuda, to je F(z)=sinz-zcosz , dakle integral ne ovisi o putu, samo o krajnjim točkama, pa je onda
integral=F(1+i)-F(0)={uvrsti se gore}=...
edit: ispravljen minus
| anab (napisa): |
2)Integral(zsinzdz) i integral ide po dijelu pravca od tocke z1=0 do z2=1+i |
f(z)=zsinz ima primitivnu svuda, to je F(z)=sinz-zcosz , dakle integral ne ovisi o putu, samo o krajnjim točkama, pa je onda
integral=F(1+i)-F(0)={uvrsti se gore}=...
edit: ispravljen minus
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy 
Zadnja promjena: Luuka; 19:10 uto, 21. 4. 2009; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Liddy
Forumaš(ica)


Pridružen/a: 17. 08. 2004. (10:03:41)
Postovi: (169)16
|
|
| [Vrh] |
|
st_fisher
Forumaš(ica)

Pridružen/a: 12. 02. 2009. (02:15:15)
Postovi: (E)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
nlo
Forumaš(ica)

Pridružen/a: 10. 12. 2008. (10:05:44)
Postovi: (3C)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
st_fisher
Forumaš(ica)

Pridružen/a: 12. 02. 2009. (02:15:15)
Postovi: (E)16
|
|
| [Vrh] |
|
desire
Forumaš(ica)


Pridružen/a: 06. 09. 2007. (07:46:21)
Postovi: (133)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 20:39 uto, 21. 4. 2009 Naslov: Postano: 20:39 uto, 21. 4. 2009 Naslov: |
    |
|
|
[quote="st_fisher"]znam da je vjerovatno lagano, al nikako mi ne ide pa molim da mi neko rješi 1.b sa kolokvija[/quote]
Lako se dobije da je
[latex]\frac{1}{z}=\frac{x-yi}{x^2+y^2}[/latex]
paramatrizacija segmenta od 1 do 1+i je:
[latex]\gamma(t)=(1,t)[/latex] tj, [latex]\gamma(t)=1+ti[/latex] za te[0,1]
i sad integriramo:
[latex]\int_{\gamma}{fdz}=\int_{0}^{1}{ (\frac{1}{t^2+1}\cdot 0 - \frac{t}{t^2+1} \cdot 1})dt}+i \int_{0}^{1}{ (\frac{1}{t^2+1}\cdot 1 + \frac{t}{t^2+1} \cdot 0})dt} =[/latex]
[latex]= \frac{1}{2} ln2 + i \cdot \frac{\pi}{4}[/latex]
[quote="st_fisher"]
i ovo također: odredi domenu funkcije f(z) = ln (z*z + z)[/quote]
Ovo bi ja ovako:
[latex]f(z) = ln (z^2 + z)=lnz+ln(z+1)[/latex]
pa je domena C bez zraka x<0 i x<-1. Jel to ok?
@desire U pravu si. Ja sam uredno pokratio x i y, pa zaboravio taj slučaj... dakle derivabilne samo na osima. :D
| st_fisher (napisa): | | znam da je vjerovatno lagano, al nikako mi ne ide pa molim da mi neko rješi 1.b sa kolokvija |
Lako se dobije da je
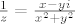
paramatrizacija segmenta od 1 do 1+i je:
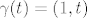 tj, tj, 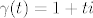 za te[0,1] za te[0,1]
i sad integriramo:
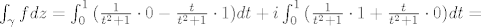
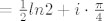
| st_fisher (napisa): |
i ovo također: odredi domenu funkcije f(z) = ln (z*z + z) |
Ovo bi ja ovako:
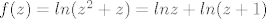
pa je domena C bez zraka x<0 i x←1. Jel to ok?
@desire U pravu si. Ja sam uredno pokratio x i y, pa zaboravio taj slučaj... dakle derivabilne samo na osima. 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
woodstock
Forumaš(ica)


Pridružen/a: 10. 11. 2006. (23:52:04)
Postovi: (99)16
Spol: 
|
|
| [Vrh] |
|
svizac
Forumaš(ica)

Pridružen/a: 11. 10. 2006. (20:59:52)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
ß
Forumaš(ica)
Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
|
| [Vrh] |
|
matmih
Forumaš(ica)


Pridružen/a: 07. 12. 2006. (22:57:42)
Postovi: (1A4)16
Spol: 
Lokacija: {Zg, De , Ri}
|
|
| [Vrh] |
|
ß
Forumaš(ica)

Pridružen/a: 29. 07. 2006. (15:29:06)
Postovi: (115)16
Spol: 
Lokacija: Graveyard Mountain Home
|
|
| [Vrh] |
|
|


















