| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
 Postano: 12:32 čet, 23. 4. 2009 Naslov: Postano: 12:32 čet, 23. 4. 2009 Naslov: |
    |
|
|
polumjer opisane kružnice je R=c/2, a upisane r=ab/a+b+c.
dakle,zbroj promjera je
2R+2r=c+2ab/(a+b+c)
umjesto c uvrstiš sqrt(a^2+b^2),umjesto a uvrsti 10-b, isto tako a^2+b^2=100-2ab (kad kvadriraš a+b=10 i središ)
dakle,dobiješ
2r+2R=korijen od(100-2a(10-a)) + 2a(10-a)/(10+korijen od(100-2a(10-a)))
svedeš na zajednički nazivnik,pokrate se -2a(10-a) i +2a(10-a),izlučiš 10 iz preostalog i pokratit će se korijeni i ispada 2r+2R=10
ja se nadam da sam dobro riješila..
polumjer opisane kružnice je R=c/2, a upisane r=ab/a+b+c.
dakle,zbroj promjera je
2R+2r=c+2ab/(a+b+c)
umjesto c uvrstiš sqrt(a^2+b^2),umjesto a uvrsti 10-b, isto tako a^2+b^2=100-2ab (kad kvadriraš a+b=10 i središ)
dakle,dobiješ
2r+2R=korijen od(100-2a(10-a)) + 2a(10-a)/(10+korijen od(100-2a(10-a)))
svedeš na zajednički nazivnik,pokrate se -2a(10-a) i +2a(10-a),izlučiš 10 iz preostalog i pokratit će se korijeni i ispada 2r+2R=10
ja se nadam da sam dobro riješila..
_________________
u raju je lijepo,ali u paklu je ekipa
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 12:45 čet, 23. 4. 2009 Naslov: Re: zadatak iz kolokvija-pomoć Postano: 12:45 čet, 23. 4. 2009 Naslov: Re: zadatak iz kolokvija-pomoć |
    |
|
|
[quote="tidus"]Zbroj kateta u pravokutnom trokutu je 10. Koliki je zbroj promjera upisane i opisane kruznice tom trokutu?[/quote]
neka je [latex]ABC[/latex] trokut sa pravim kutem u [latex]C[/latex]
neka je [latex]S[/latex] srediste upisane mu kruznice, neka su [latex]A_1, B_1, C_1[/latex] redom diralista upisane kruznice i trokuta na stranicama [latex]\overline{AC},\overline{BC},\overline{BA}[/latex] tada je [latex]|\overline{SA_1}|=|\overline{SB_1}|=|\overline{SC_1}|=:\rho, R=c/2, 2(\rho+R)=?[/latex]
[latex]a:=|\overline{BC}|, b:=|\overline{AC}|, c:=|\overline{AB}|[/latex]
[latex]|\overline{BB_1}|=a-\rho=|\overline{BC_1}|\Rightarrow |\overline{C_1A}|=c-a+\rho=|\overline{AA_1}|=b-\rho[/latex]
[latex]b+a=2\rho + c=2\rho +2R=10[/latex]
| tidus (napisa): | | Zbroj kateta u pravokutnom trokutu je 10. Koliki je zbroj promjera upisane i opisane kruznice tom trokutu? |
neka je 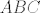 trokut sa pravim kutem u trokut sa pravim kutem u 
neka je  srediste upisane mu kruznice, neka su srediste upisane mu kruznice, neka su 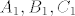 redom diralista upisane kruznice i trokuta na stranicama redom diralista upisane kruznice i trokuta na stranicama 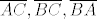 tada je tada je 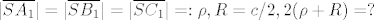
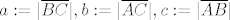
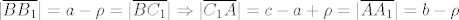
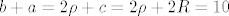
_________________
Mario Berljafa
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 18:37 čet, 23. 4. 2009 Naslov: Postano: 18:37 čet, 23. 4. 2009 Naslov: |
    |
|
|
Dan je pravokutni trokut [latex]ABC[/latex] s pravim kutem pri vrhu [latex]C[/latex]. Neka je [latex]U[/latex] središte upisane, a [latex]O[/latex] središte opisane mu kružnice. Označimo [latex]\left|AB\right|=c[/latex], [latex]\left|BC\right|=a[/latex], [latex]\left|CA\right|=b[/latex], [latex]r[/latex] neka je polumjer upisane, a [latex]R[/latex] opisane kružnice trokutu [latex]ABC[/latex]. Neka su dalje točke [latex]D[/latex], [latex]E[/latex], [latex]F[/latex] redom dirališta stranica [latex]\overline{AB}[/latex], [latex]\overline{BC}[/latex], [latex]\overline{CA}[/latex] trokuta [latex]ABC[/latex] s upisanom mu kružnicom.
Četverokut [latex]CFUE[/latex] je očito kvadrat, pa vrijedi da je [latex]\left|CE\right|=\left|CF\right|=r[/latex]. Dalje, znamo da je [latex]\left|AF\right|=\left|AD\right|=x[/latex], te [latex]\left|BD\right|=\left|BE\right|=y[/latex].
Sada vidimo da je [latex]a+b=y+r+r+x=2r+x+y=2r+c \Longrightarrow r = \frac{a+b-c}{2}[/latex].
Neka je [latex]P[/latex] polovište hipotenuze [latex]\overline{AB}[/latex] trokuta [latex]ABC[/latex], konstruirajmo kružnicu polumjera [latex]\left|PA\right|[/latex] sa središtem u [latex]P[/latex], sada prema Talesovom teoremu vidimo da točka [latex]C[/latex] leži na toj istoj kružnici. Zbog svega toga je [latex]O \equiv P[/latex]. Sada je odmah jasno da je [latex]R=\frac{c}{2}[/latex].
Još jedan od načina na koji možemo izraziti [latex]r[/latex] i [latex]R[/latex] je da pogledamo formule za površinu pravokutnog trokuta, naime, vrijedi [latex]p\left(ABC\right)=\frac{ab}{2}=rs=\frac{abc}{4R}[/latex], gdje je [latex]s=\frac{a+b+c}{2}[/latex] (zadnje dvije formule vrijede za bilo koji trokut).
Sada je odmah jasno da vrijedi [latex]r=\frac{ab}{a+b+c}[/latex].
Dan je pravokutni trokut 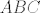 s pravim kutem pri vrhu s pravim kutem pri vrhu  . Neka je . Neka je 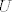 središte upisane, a središte upisane, a 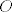 središte opisane mu kružnice. Označimo središte opisane mu kružnice. Označimo 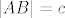 , , 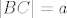 , , 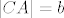 , ,  neka je polumjer upisane, a neka je polumjer upisane, a 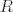 opisane kružnice trokutu opisane kružnice trokutu 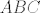 . Neka su dalje točke . Neka su dalje točke 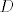 , , 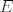 , , 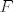 redom dirališta stranica redom dirališta stranica 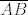 , , 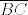 , , 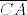 trokuta trokuta 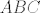 s upisanom mu kružnicom. s upisanom mu kružnicom.
Četverokut 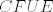 je očito kvadrat, pa vrijedi da je je očito kvadrat, pa vrijedi da je 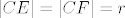 . Dalje, znamo da je . Dalje, znamo da je 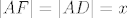 , te , te 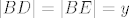 . .
Sada vidimo da je 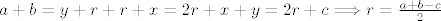 . .
Neka je  polovište hipotenuze polovište hipotenuze 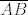 trokuta trokuta 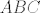 , konstruirajmo kružnicu polumjera , konstruirajmo kružnicu polumjera 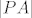 sa središtem u sa središtem u  , sada prema Talesovom teoremu vidimo da točka , sada prema Talesovom teoremu vidimo da točka  leži na toj istoj kružnici. Zbog svega toga je leži na toj istoj kružnici. Zbog svega toga je 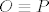 . Sada je odmah jasno da je . Sada je odmah jasno da je  . .
Još jedan od načina na koji možemo izraziti  i i 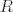 je da pogledamo formule za površinu pravokutnog trokuta, naime, vrijedi je da pogledamo formule za površinu pravokutnog trokuta, naime, vrijedi 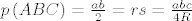 , gdje je , gdje je 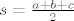 (zadnje dvije formule vrijede za bilo koji trokut). (zadnje dvije formule vrijede za bilo koji trokut).
Sada je odmah jasno da vrijedi 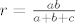 . .
|
|
| [Vrh] |
|
bad_angel
Forumaš(ica)


Pridružen/a: 01. 11. 2008. (18:30:25)
Postovi: (43)16
Lokacija: svugdje po malo
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Falva_Equa
Forumaš(ica)


Pridružen/a: 17. 11. 2008. (22:22:39)
Postovi: (8)16
Spol: 
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
bimar
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (14:45:25)
Postovi: (61)16
Lokacija: arkadija
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
|














