| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
alma
Forumaš(ica)

Pridružen/a: 03. 01. 2007. (19:38:37)
Postovi: (26)16
Spol: 
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
alma
Forumaš(ica)

Pridružen/a: 03. 01. 2007. (19:38:37)
Postovi: (26)16
Spol: 
|
|
| [Vrh] |
|
barbarag
Forumaš(ica)

Pridružen/a: 27. 03. 2008. (14:54:10)
Postovi: (29)16
|
 Postano: 7:41 sri, 29. 4. 2009 Naslov: Postano: 7:41 sri, 29. 4. 2009 Naslov: |
    |
|
|
može pomoć? nikako da skužim te zadatke.. :oops:
kod zadatka phi(n)=20 imamo da je n=2^a*3^b*5^c*11^d, a=0,1,2, b=0,1, c=0,1,2 i d=0,1.
najprije provjeravamo za n=11k i dobijemo da je n=33,44,66. Do tud kužim, ali za koji n provjeravamo slijedeće? n=5k ili n=3k ili nešto treće?
I je li u ovom zadatku k=2^x*5^y? (jer je 20=2*2*5)
može pomoć? nikako da skužim te zadatke.. 
kod zadatka phi(n)=20 imamo da je n=2^a*3^b*5^c*11^d, a=0,1,2, b=0,1, c=0,1,2 i d=0,1.
najprije provjeravamo za n=11k i dobijemo da je n=33,44,66. Do tud kužim, ali za koji n provjeravamo slijedeće? n=5k ili n=3k ili nešto treće?
I je li u ovom zadatku k=2^x*5^y? (jer je 20=2*2*5)
_________________
uvijek postoje iznimke!
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 10:25 sri, 29. 4. 2009 Naslov: Postano: 10:25 sri, 29. 4. 2009 Naslov: |
    |
|
|
[quote="barbarag"]može pomoć? nikako da skužim te zadatke.. :oops:
kod zadatka varphi(n)=20 imamo da je n=2^a*3^b*5^c*11^d, a=0,1,2, b=0,1, c=0,1,2 i d=0,1.
najprije provjeravamo za n=11k i dobijemo da je n=33,44,66. Do tud kužim, ali za koji n provjeravamo slijedeće? n=5k ili n=3k ili nešto treće?
I je li u ovom zadatku k=2^x*5^y? (jer je 20=2*2*5)[/quote]
Pa mozes kako hoces provjeravati, ali trebas paziti da ne profulas neki slucaj, pa je mozda najbolje da ides po redu.
Za pocetak ce ti pomoci ova trivijalna cinjenica:
[latex]\varphi(p^k) = \varphi(p) p^{k - 1} = p^{k-1} ( p - 1) = p^k - p[/latex], za svaki prosti broj [latex]p[/latex]. Dakle sad znamo da je:
[latex]\varphi(2^a) = 2^{a - 1}, \varphi(3^b) = 2 \cdot 3^{b - 1}[/latex], za [latex]a >0, b > 0[/latex].
Sad idemo rjesavati dalje:
[latex]\varphi(5) = 4 \Rightarrow \varphi(2^a + 3^b) = 5[/latex], odmah vidimo da to ne mozemo postici.
[latex]\varphi(25) = 20[/latex] tu je lako, rjesenja su dakle 25 i 50 jer [latex]\varphi(2) = 1[/latex].
Ostalo nam je jos provjeriti za [latex] n = 2^a 3 ^ b[/latex], ali kako broj 20 ima prosti faktor 5, iz gornjeg razmatranja vidimo da tu ne postoji nijedno rjesenje.
Samo bih htio napomenuti da nisam jos rjesavao zadatke ovakvog tipa pa je moguce da sam nesto krivo rekao, pa molim kolege da ako uoce nesto krivo da me isprave.
| barbarag (napisa): | može pomoć? nikako da skužim te zadatke.. 
kod zadatka varphi(n)=20 imamo da je n=2^a*3^b*5^c*11^d, a=0,1,2, b=0,1, c=0,1,2 i d=0,1.
najprije provjeravamo za n=11k i dobijemo da je n=33,44,66. Do tud kužim, ali za koji n provjeravamo slijedeće? n=5k ili n=3k ili nešto treće?
I je li u ovom zadatku k=2^x*5^y? (jer je 20=2*2*5) |
Pa mozes kako hoces provjeravati, ali trebas paziti da ne profulas neki slucaj, pa je mozda najbolje da ides po redu.
Za pocetak ce ti pomoci ova trivijalna cinjenica:
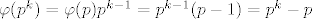 , za svaki prosti broj , za svaki prosti broj  . Dakle sad znamo da je: . Dakle sad znamo da je:
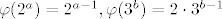 , za , za 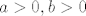 . .
Sad idemo rjesavati dalje:
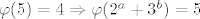 , odmah vidimo da to ne mozemo postici. , odmah vidimo da to ne mozemo postici.
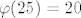 tu je lako, rjesenja su dakle 25 i 50 jer tu je lako, rjesenja su dakle 25 i 50 jer 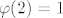 . .
Ostalo nam je jos provjeriti za 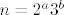 , ali kako broj 20 ima prosti faktor 5, iz gornjeg razmatranja vidimo da tu ne postoji nijedno rjesenje. , ali kako broj 20 ima prosti faktor 5, iz gornjeg razmatranja vidimo da tu ne postoji nijedno rjesenje.
Samo bih htio napomenuti da nisam jos rjesavao zadatke ovakvog tipa pa je moguce da sam nesto krivo rekao, pa molim kolege da ako uoce nesto krivo da me isprave.
_________________
Bri
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 13:21 sri, 29. 4. 2009 Naslov: Postano: 13:21 sri, 29. 4. 2009 Naslov: |
    |
|
|
ajd idem ja od početka... fi(n)=20=2*2*5.
znamo da je za
[latex]n=p_1^{\alpha_1} \cdot p_2^{\alpha_2} \cdot ... \cdot p_r^{\alpha_r} [/latex]
[latex]\phi (n)=p_1^{\alpha_1-1}(p_1-1) \cdot p_2^{\alpha_2}(p_2-1) \cdot ... \cdot p_r^{\alpha_r}(p_r-1) [/latex]
iz toga se vidi da svaki p prosti fator od n mora biti takav da p-1 dijeli fi(n).
iz tog slijedi: pi e { 2,3,5,11}
sada promatramo razne kombinacije...
1. n=11k (11 i k su rel prosti jer ako nisu onda je potencija od 11 barem 2 kod prikaza od n->11 dijeli 20 a to nije)
na to djelujemo fjom fi koja je multiplikativna za rel proste brojeve...
dobijemo 20=10*fi(k) -> fi(k)=2 -> k=3,4,6 -> n=33,44,66
I nakon ovog slučaja, kad se dođe do dijela kad ostanu 3 broja, bez puno razmišljanja se mogu provjerit sve kombinacije
dakle brojevi oblika 5^a, 2^a, 3^a, 5^a 2^b, 5^a 3^b, 2^a 3^b, 2^a 3^b 5^c. U dosta njih se dobije kontradikcija i to je to.
ajd idem ja od početka... fi(n)=20=2*2*5.
znamo da je za
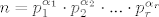
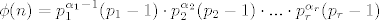
iz toga se vidi da svaki p prosti fator od n mora biti takav da p-1 dijeli fi(n).
iz tog slijedi: pi e { 2,3,5,11}
sada promatramo razne kombinacije...
1. n=11k (11 i k su rel prosti jer ako nisu onda je potencija od 11 barem 2 kod prikaza od n→11 dijeli 20 a to nije)
na to djelujemo fjom fi koja je multiplikativna za rel proste brojeve...
dobijemo 20=10*fi(k) → fi(k)=2 → k=3,4,6 → n=33,44,66
I nakon ovog slučaja, kad se dođe do dijela kad ostanu 3 broja, bez puno razmišljanja se mogu provjerit sve kombinacije
dakle brojevi oblika 5^a, 2^a, 3^a, 5^a 2^b, 5^a 3^b, 2^a 3^b, 2^a 3^b 5^c. U dosta njih se dobije kontradikcija i to je to.
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
|








