| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
 Postano: 13:00 sri, 13. 5. 2009 Naslov: Postano: 13:00 sri, 13. 5. 2009 Naslov: |
    |
|
|
Pokusaj izraziti volumen stošca pomoću kuta alfa, uzmi u obzir da mozes bez smanjenja opcenitosti uzeti da ti je radijus kruznice 1 (jer ti se ne trazi tocan volumen, vec samo alfa za koji ce volumen biti najveci), uz malo pitagorinih poucaka nadjes takvu f-ju. Deriviras ju, nadjes stacionarne tocke, uzmes u obzir i ostale kriticne tocke ako postoje i sve te tocke uvrstis u f-ju da vidis koji je globalni maksimum na intervalu od [0, pi]
Pokusaj izraziti volumen stošca pomoću kuta alfa, uzmi u obzir da mozes bez smanjenja opcenitosti uzeti da ti je radijus kruznice 1 (jer ti se ne trazi tocan volumen, vec samo alfa za koji ce volumen biti najveci), uz malo pitagorinih poucaka nadjes takvu f-ju. Deriviras ju, nadjes stacionarne tocke, uzmes u obzir i ostale kriticne tocke ako postoje i sve te tocke uvrstis u f-ju da vidis koji je globalni maksimum na intervalu od [0, pi]
_________________
reductio ad absurdum
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 13:44 sri, 13. 5. 2009 Naslov: Postano: 13:44 sri, 13. 5. 2009 Naslov: |
    |
|
|
ne trebas stavit da je r=1, nije da smeta, al bas ti nis ne pomaze...
duljina luka isjecka je opseg baze stosca, a radijus kruznice (isjecka) neznam kako se zove, mozda izvodnica stosca... uglavnom znam da se to oznacavalo sa s, ako pomaze
sve to kao i visinu izrazis pomocu alfa i r i deriviras po alfa
rjesenje neznam zasto bi bilo iz intervala [0,pi], rjesenje je ocito iz intervala <0,2pi>
meni ispadne [latex]\frac{2\pi\sqrt{6}}{3}[/latex]
ne trebas stavit da je r=1, nije da smeta, al bas ti nis ne pomaze...
duljina luka isjecka je opseg baze stosca, a radijus kruznice (isjecka) neznam kako se zove, mozda izvodnica stosca... uglavnom znam da se to oznacavalo sa s, ako pomaze
sve to kao i visinu izrazis pomocu alfa i r i deriviras po alfa
rjesenje neznam zasto bi bilo iz intervala [0,pi], rjesenje je ocito iz intervala <0,2pi>
meni ispadne 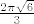
_________________
Mario Berljafa
|
|
| [Vrh] |
|
JANKRI
Forumaš(ica)

Pridružen/a: 10. 07. 2008. (02:30:58)
Postovi: (10F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
Grga
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: 
|
 Postano: 21:40 sri, 13. 5. 2009 Naslov: Postano: 21:40 sri, 13. 5. 2009 Naslov: |
    |
|
|
Izrezemo iz kruznice isjecak sa kutem [latex]\alpha[/latex] i savijemo u stozac. Baza tog stosca je krug ciji je rub kriznica opsega
[latex]\frac{\alpha}{2 \pi}2r \pi = \alpha r[/latex]
Znaci da je radijus tog kruga [latex]\frac{\alpha r}{2 \pi}[/latex]
Ono sto ne znam kako se zove, kao ni kolega gore :) , a radi se o duzini koja spaja vrh stosca i tocku na rubu baze je duljine [latex]r[/latex].
Znaci da je visina stosca
[latex]\sqrt{r^2 - (\frac{\alpha r}{2 \pi})^2} = \frac{r \sqrt{4 \pi^2 - \alpha^2}}{2\pi}[/latex]
Od tuda je visina
[latex]f(\alpha) = \frac{1}{3} (\frac{\alpha r}{2 \pi})^2 \pi \frac{r \sqrt{4 \pi^2 - \alpha^2}}{2\pi} = k \alpha^2 \sqrt{4 \pi^2 - \alpha^2}[/latex]
Gdje smo sve konstante kojima mnozimo cijeli izraz potrpali u jednu konstantu, koja je strogo veca od 0.
[latex]f > 0[/latex], pa je tocka maksimuma od [latex]f[/latex] ujedno i tocka maksimuma od [latex]g = f^2 = k^2(4 \pi^2 \alpha^4 - \alpha^6)[/latex]
[latex]g'(\alpha) = k^2(16 \pi^2 \alpha^3 - 6 \alpha^5) = 2 k^2 \alpha^3(8 \pi^2 - 3 \alpha^2)[/latex]
Kako [latex]\alpha = 0[/latex] jasno nije rjesenje, [latex]k > 0[/latex], ostaje nam rijesiti onu kvadratnu jednadzbu, a kako je [latex]\alpha > 0[/latex], dobivamo
[latex]\alpha = \frac{2 \pi \sqrt{6}}{3}[/latex]
(kako je i Gino rekao, a vece je od pi tako da pretpostavka druogg kolege ne stoji)
Da se radi o maksimumu je jasno iz cinjenice da za krajnje vrijednosti kuta dobivamo volumen 0
Izrezemo iz kruznice isjecak sa kutem  i savijemo u stozac. Baza tog stosca je krug ciji je rub kriznica opsega i savijemo u stozac. Baza tog stosca je krug ciji je rub kriznica opsega
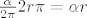
Znaci da je radijus tog kruga 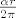
Ono sto ne znam kako se zove, kao ni kolega gore  , a radi se o duzini koja spaja vrh stosca i tocku na rubu baze je duljine , a radi se o duzini koja spaja vrh stosca i tocku na rubu baze je duljine  . .
Znaci da je visina stosca
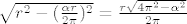
Od tuda je visina
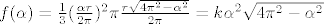
Gdje smo sve konstante kojima mnozimo cijeli izraz potrpali u jednu konstantu, koja je strogo veca od 0.
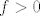 , pa je tocka maksimuma od , pa je tocka maksimuma od  ujedno i tocka maksimuma od ujedno i tocka maksimuma od 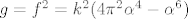
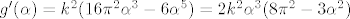
Kako  jasno nije rjesenje, jasno nije rjesenje, 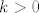 , ostaje nam rijesiti onu kvadratnu jednadzbu, a kako je , ostaje nam rijesiti onu kvadratnu jednadzbu, a kako je 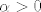 , dobivamo , dobivamo
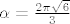
(kako je i Gino rekao, a vece je od pi tako da pretpostavka druogg kolege ne stoji)
Da se radi o maksimumu je jasno iz cinjenice da za krajnje vrijednosti kuta dobivamo volumen 0
_________________
Bri
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
|












