|
[quote="Gino"]vjerujem da ce ti se autor javit sam :D :D[/quote]
Evo, javljam se :D
Nadam se da neće biti problema radi pisanja rješenja zadatka iz zadaće na forumu. :)
[b]Zadatak:[/b] Neka je [latex]V[/latex] konačnodimenzionalan vektorski prostor, te neka je [latex]A \in L\left(V\right)[/latex] operator takav da vrijedi [latex]AB = BA \textrm{,}\, \forall B \in L\left(V\right)[/latex]. Dokažite da tada postoji skalar [latex]\alpha[/latex] takav da je [latex]A=\alpha I[/latex]. (Uputa: pokažite da [latex]A[/latex] ima bar jednu svojstvenu vrijednost i promatrajte odgovarajući svojstveni potprostor. Prethodno pokažite da je svaki svojstveni potprostor operatora [latex]T \in L\left(V\right)[/latex] invarijantan za sve operatore [latex]S \in L\left(V\right)[/latex] koji komutiraju s [latex]T[/latex].)
Najprije da kažem da u dokazu ne koristim u zadatku danu uputu (barem ne direktno).
Krenimo, uočimo da ako je [latex]\dim{V} \leq 1[/latex] da je tvrdnja zadatka očita. Dalje radimo s pretpostavkom da je [latex]\dim{V} \geq 2[/latex]. Dalje je ideja sljedeća. Najprije ću pokazati da ako je [latex]Ax=y[/latex], za neke [latex]x,\,y \in V[/latex] da je tada skup [latex]\left\{x,\,y\right\}[/latex] linearno zavisan. Odnosno, za svaki vektor [latex]x \in V[/latex] vrijedi da je [latex]Ax=\alpha_xx[/latex], za neki skalar [latex]\alpha_x[/latex]. Nakon toga je još potrebno pokazati da je [latex]\alpha_x=\alpha[/latex] za neki skalar [latex]\alpha[/latex] i to za svaki vektor [latex]x \in V[/latex], tj. da je taj skalar uvijek isti, to onda točno znači da je [latex]A=\alpha I[/latex].
Kako je [latex]\dim{V} \geq 2[/latex] možemo izabrati [latex]x,\,y \in V[/latex] koji čine linearno nezavisan skup i taj skup nadopuniti do baze za [latex]V[/latex], neka je tada [latex]\left\{x,\, y,\, e_3,\, \ldots,\, e_n\right\}[/latex] baza za [latex]V[/latex].
Pretpostavimo da je [latex]Ax=y[/latex]. Definirajmo operatore [latex]B \in L\left(V\right)[/latex] i [latex]B' \in L\left(V\right)[/latex] na sljedeći način:
[latex]Bx=y[/latex], [latex]By=x[/latex], [latex]Be_i=0,\, \forall i \in \left\{3,\, 4,\, \ldots,\, n\right\}[/latex].
[latex]B'x=x[/latex], [latex]B'y=x[/latex], [latex]B'e_i=0,\, \forall i \in \left\{3,\, 4,\, \ldots,\, n\right\}[/latex].
Sada vrijedi:
[latex]A\left(Bx\right)=B\left(Ax\right) \Longrightarrow Ay = By \Longrightarrow Ay = x[/latex],
[latex]A\left(B'y\right)=B'\left(Ay\right) \Longrightarrow Ax = B'x \Longrightarrow y=x[/latex]. [latex]\Rightarrow\Leftarrow[/latex]
Došli smo do kontradikcije, dakle, ako je za [latex]x,\, y \in V[/latex], [latex]Ax=y[/latex], onda je skup [latex]\left\{x,\, y\right\}[/latex] nužno zavisan. Ovime smo pokazali da za svaki [latex]x \in V[/latex] postoji skalar [latex]\alpha_x[/latex] takav da je [latex]Ax = \alpha_xx[/latex]. Pokažimo sada da je taj skalar isti za svaki vektor [latex]x \in V[/latex].
Neka su najprije [latex]x,\, y \in V \setminus \left\{0\right\}[/latex] takvi da postoji skalar [latex]\lambda[/latex] takav da je [latex]y = \lambda x[/latex]. Znamo da postoje skalari [latex]\alpha_x[/latex] i [latex]\alpha_y[/latex] takvi da je [latex]Ax=\alpha_xx[/latex] i [latex]Ay=\alpha_yy[/latex].
[latex]\alpha_yy=Ay=A\left(\lambda x\right)=\lambda Ax = \lambda \alpha_xx = \alpha_x \lambda x = \alpha_x y \Longrightarrow \alpha_y= \alpha_x[/latex].
Sada, neka su [latex]x,\, y \in V[/latex] takvi da je skup [latex]\left\{x,\, y\right\}[/latex] linearno nezavisan. Vrijedi
[latex]Ax=\alpha_xx[/latex],
[latex]Ay=\alpha_yy[/latex],
[latex]A\left(x-y\right)=\alpha_{x-y}\left(x-y\right)[/latex],
za neke skalare [latex]\alpha_x[/latex], [latex]\alpha_y[/latex], [latex]\alpha_{x-y}[/latex].
Sada je
[latex]\alpha_{x-y}\left(x-y\right)=A\left(x-y\right)=Ax - Ay = \alpha_xx - \alpha_yy[/latex]
[latex]\Longrightarrow \left(\alpha_x-\alpha_{x-y}\right)x + \left(\alpha_{x-y}-\alpha_y\right)y = 0[/latex].
Kako je skup [latex]\left\{x,\, y\right\}[/latex] nezavisan, konačno dobivamo [latex]\alpha_x=\alpha_{x-y}=\alpha_y[/latex] što smo i željeli pokazati.
Ovime smo pokazali da postoji skalar [latex]\alpha[/latex] takav da je [latex]Ax=\alpha x[/latex], za svaki [latex]x \in V[/latex] (tvrdnja, naravno vrijedi i za [latex]x=0[/latex], jer je [latex]A0=0[/latex], za bilo koji operator [latex]A[/latex]), odnosno, da je [latex]A=\alpha I[/latex].
[b]Q.E.D.[/b]
| Gino (napisa): | vjerujem da ce ti se autor javit sam   |
Evo, javljam se 
Nadam se da neće biti problema radi pisanja rješenja zadatka iz zadaće na forumu. 
Zadatak: Neka je 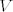 konačnodimenzionalan vektorski prostor, te neka je konačnodimenzionalan vektorski prostor, te neka je 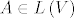 operator takav da vrijedi operator takav da vrijedi 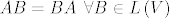 . Dokažite da tada postoji skalar . Dokažite da tada postoji skalar  takav da je takav da je 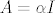 . (Uputa: pokažite da . (Uputa: pokažite da  ima bar jednu svojstvenu vrijednost i promatrajte odgovarajući svojstveni potprostor. Prethodno pokažite da je svaki svojstveni potprostor operatora ima bar jednu svojstvenu vrijednost i promatrajte odgovarajući svojstveni potprostor. Prethodno pokažite da je svaki svojstveni potprostor operatora 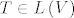 invarijantan za sve operatore invarijantan za sve operatore 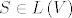 koji komutiraju s koji komutiraju s  .) .)
Najprije da kažem da u dokazu ne koristim u zadatku danu uputu (barem ne direktno).
Krenimo, uočimo da ako je 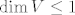 da je tvrdnja zadatka očita. Dalje radimo s pretpostavkom da je da je tvrdnja zadatka očita. Dalje radimo s pretpostavkom da je 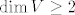 . Dalje je ideja sljedeća. Najprije ću pokazati da ako je . Dalje je ideja sljedeća. Najprije ću pokazati da ako je 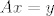 , za neke , za neke 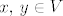 da je tada skup da je tada skup 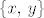 linearno zavisan. Odnosno, za svaki vektor linearno zavisan. Odnosno, za svaki vektor 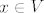 vrijedi da je vrijedi da je 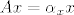 , za neki skalar , za neki skalar 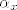 . Nakon toga je još potrebno pokazati da je . Nakon toga je još potrebno pokazati da je 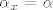 za neki skalar za neki skalar  i to za svaki vektor i to za svaki vektor 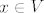 , tj. da je taj skalar uvijek isti, to onda točno znači da je , tj. da je taj skalar uvijek isti, to onda točno znači da je 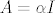 . .
Kako je 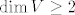 možemo izabrati možemo izabrati 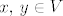 koji čine linearno nezavisan skup i taj skup nadopuniti do baze za koji čine linearno nezavisan skup i taj skup nadopuniti do baze za 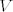 , neka je tada , neka je tada 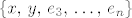 baza za baza za 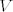 . .
Pretpostavimo da je 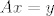 . Definirajmo operatore . Definirajmo operatore 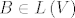 i i 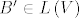 na sljedeći način: na sljedeći način:
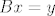 , , 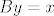 , , 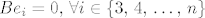 . .
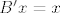 , , 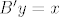 , , 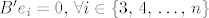 . .
Sada vrijedi:
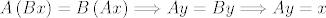 , ,
 . . 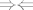
Došli smo do kontradikcije, dakle, ako je za 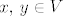 , , 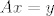 , onda je skup , onda je skup 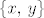 nužno zavisan. Ovime smo pokazali da za svaki nužno zavisan. Ovime smo pokazali da za svaki 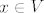 postoji skalar postoji skalar 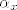 takav da je takav da je 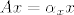 . Pokažimo sada da je taj skalar isti za svaki vektor . Pokažimo sada da je taj skalar isti za svaki vektor 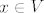 . .
Neka su najprije 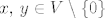 takvi da postoji skalar takvi da postoji skalar  takav da je takav da je 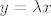 . Znamo da postoje skalari . Znamo da postoje skalari 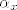 i i 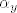 takvi da je takvi da je 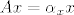 i i 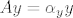 . .
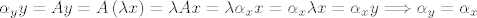 . .
Sada, neka su 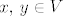 takvi da je skup takvi da je skup 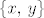 linearno nezavisan. Vrijedi linearno nezavisan. Vrijedi
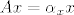 , ,
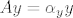 , ,
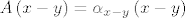 , ,
za neke skalare 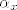 , , 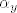 , , 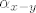 . .
Sada je
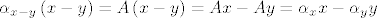
 . .
Kako je skup 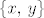 nezavisan, konačno dobivamo nezavisan, konačno dobivamo 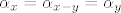 što smo i željeli pokazati. što smo i željeli pokazati.
Ovime smo pokazali da postoji skalar  takav da je takav da je 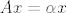 , za svaki , za svaki 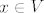 (tvrdnja, naravno vrijedi i za (tvrdnja, naravno vrijedi i za  , jer je , jer je 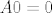 , za bilo koji operator , za bilo koji operator  ), odnosno, da je ), odnosno, da je 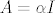 . .
Q.E.D.
|










