| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
tidus
Forumaš(ica)


Pridružen/a: 16. 02. 2009. (12:47:59)
Postovi: (A5)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
 Postano: 17:21 ned, 14. 6. 2009 Naslov: Postano: 17:21 ned, 14. 6. 2009 Naslov: |
    |
|
|
hm... sumnjiv mi je malo ovaj drugi zadatak...
Recimo ovako:
Neka imamo bilo kakav operator A za kojeg vrijedi: x okomito na y => Ax okomito na Ay.
Uzimo bilo koju ortonormiranu bazu za V (sigurno postoji zbog GS.ovog postupka) e = {e1, e2, ..., en}
Recimo da je Ae_k = 0. Time ne narusavamo uvjet zadatka jer je nula okomit na svaki vektor.
Sada, kada bi vrijedilo da postoji ß iz R t.d. A = ßU sljedilo bi da je
Ae_k = ßUe_k, odnosno
0 = ßUe_k.
Pošto unitaran operator ortonormiranu bazu prevodi u ortonormiranu bazu, zaključujemo da Ue_k nikako nije 0 (e_k - je element ortonormirane baze), dakle ß = 0.
Odnosno, A = ßU = 0, što je očito kontradikcija, jer A ne mora biti 0.
Valjda u necemu grijesim.. pa bih molio nekog da me ispravi.
hm... sumnjiv mi je malo ovaj drugi zadatak...
Recimo ovako:
Neka imamo bilo kakav operator A za kojeg vrijedi: x okomito na y => Ax okomito na Ay.
Uzimo bilo koju ortonormiranu bazu za V (sigurno postoji zbog GS.ovog postupka) e = {e1, e2, ..., en}
Recimo da je Ae_k = 0. Time ne narusavamo uvjet zadatka jer je nula okomit na svaki vektor.
Sada, kada bi vrijedilo da postoji ß iz R t.d. A = ßU sljedilo bi da je
Ae_k = ßUe_k, odnosno
0 = ßUe_k.
Pošto unitaran operator ortonormiranu bazu prevodi u ortonormiranu bazu, zaključujemo da Ue_k nikako nije 0 (e_k - je element ortonormirane baze), dakle ß = 0.
Odnosno, A = ßU = 0, što je očito kontradikcija, jer A ne mora biti 0.
Valjda u necemu grijesim.. pa bih molio nekog da me ispravi.
_________________
reductio ad absurdum
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
Gino
Forumaš(ica)

Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Lokacija: Pula
|
 Postano: 20:09 pon, 15. 6. 2009 Naslov: Postano: 20:09 pon, 15. 6. 2009 Naslov: |
    |
|
|
pa je da, ako je [latex]Ae_k=0[/latex] za neko [latex]k[/latex], onda je [latex]Ae_k=0, \forall k[/latex] (to sljedi iz moje ideje o rjesavanju zadatka :D )
sad mi jos ne pada na pamet kako to dokazat al ideja bi bila
uzmes ortonormiranu bazu [latex]e=\{e_1,e_2,...,e_n\}[/latex] sada je [latex]\{Ae_1,Ae_2,...,Ae_n\}[/latex] otogonalan skup, treba samo pokazat da je [latex]\|Ae_i\|=\|Ae_j\|, \forall i,j[/latex] tada je zadatak gotov, [latex]\alpha=\|Ae_1\|[/latex], [latex]U=\displaystyle\frac{1}{\|Ae_1\|}\left[ A\right][/latex], za [latex]\|Ae_1\|\neq 0[/latex] za [latex]\|Ae_1\|=0[/latex] je npr [latex]U=I[/latex]
[latex]\left[ A\right] [/latex] je matrica ciji su stupci [latex]Ae_1, ..., Ae_n[/latex]
pitanje je samo kako dokazat da svi oni imaju iste norme
pa je da, ako je 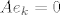 za neko za neko  , onda je , onda je 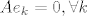 (to sljedi iz moje ideje o rjesavanju zadatka (to sljedi iz moje ideje o rjesavanju zadatka  ) )
sad mi jos ne pada na pamet kako to dokazat al ideja bi bila
uzmes ortonormiranu bazu 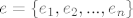 sada je sada je 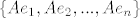 otogonalan skup, treba samo pokazat da je otogonalan skup, treba samo pokazat da je 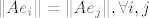 tada je zadatak gotov, tada je zadatak gotov, 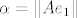 , , 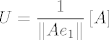 , za , za 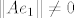 za za 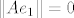 je npr je npr 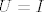
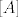 je matrica ciji su stupci je matrica ciji su stupci 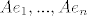
pitanje je samo kako dokazat da svi oni imaju iste norme
_________________
Mario Berljafa
|
|
| [Vrh] |
|
Novi
Forumaš(ica)

Pridružen/a: 17. 07. 2007. (12:08:32)
Postovi: (11F)16
Spol: 
|
|
| [Vrh] |
|
|









