|
Ovo je meni najcool lema u teoriji mjere, jer se na njoj temelji Lebesgueov integral.
Pretpostavimo prvo da je slika funkcije f jednaka (0,1], poanta je nekako "razbiti" taj segment na sitne dijelove i onda na tim djelovima definirati niz funkcija tako da zad. dane uvjete. Pa uzmimo [latex]n\in\mathbb{N}[/latex] neki dovoljno veliki i podijelimo spomenuti segment na [latex]2^n[/latex] jednakih dijelova dijelova, zatim definiramo skupove [latex]E_k=\{x\in X\colon f(x)\in \langle \frac{k-1}{2^n},\frac{k}{2^n}]\},~k=1,\dots,2^n[/latex], te definiramo funkciju [latex]f_n(x)=\sum_{k=1}^{2^n}\frac{k}{2^n}\chi_{E_k}[/latex] za [latex]n\in\mathbb{N}[/latex]. Sada samo treba provjeriti da taj niz doista zadovoljava dane uvjete.
Ako je rijec o [latex]\langle 0,n][/latex], onda samo imamo [latex]n2^n[/latex] skupova (jer isti postupak ponovimo na svakom [latex]\langle k-1,k],~k=1,\dots n[/latex]) i granica kod sume se promijeni. Ako pak funkcija f nije omedena tada na skupu na kojem je ona veca od [latex]n\in\mathbb{N}[/latex] stavimo da fukcija [latex]f_n[/latex] ima vrijednost [latex]n[/latex]. Ostavljam ti da rijesis detalje u dokazu.
Lagano se takoder pokaze da, ako je dana funkcija f omedena da je zapravo konvergencija konstruiranog niza uniformna.
Ovo je meni najcool lema u teoriji mjere, jer se na njoj temelji Lebesgueov integral.
Pretpostavimo prvo da je slika funkcije f jednaka (0,1], poanta je nekako "razbiti" taj segment na sitne dijelove i onda na tim djelovima definirati niz funkcija tako da zad. dane uvjete. Pa uzmimo 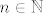 neki dovoljno veliki i podijelimo spomenuti segment na neki dovoljno veliki i podijelimo spomenuti segment na 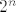 jednakih dijelova dijelova, zatim definiramo skupove jednakih dijelova dijelova, zatim definiramo skupove 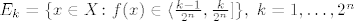 , te definiramo funkciju , te definiramo funkciju 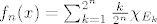 za za 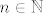 . Sada samo treba provjeriti da taj niz doista zadovoljava dane uvjete. . Sada samo treba provjeriti da taj niz doista zadovoljava dane uvjete.
Ako je rijec o 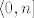 , onda samo imamo , onda samo imamo  skupova (jer isti postupak ponovimo na svakom skupova (jer isti postupak ponovimo na svakom 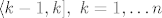 ) i granica kod sume se promijeni. Ako pak funkcija f nije omedena tada na skupu na kojem je ona veca od ) i granica kod sume se promijeni. Ako pak funkcija f nije omedena tada na skupu na kojem je ona veca od 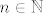 stavimo da fukcija stavimo da fukcija 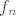 ima vrijednost ima vrijednost  . Ostavljam ti da rijesis detalje u dokazu. . Ostavljam ti da rijesis detalje u dokazu.
Lagano se takoder pokaze da, ako je dana funkcija f omedena da je zapravo konvergencija konstruiranog niza uniformna.
|






