| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 19:55 pet, 24. 4. 2009 Naslov: Operacije s kardinalitetima Postano: 19:55 pet, 24. 4. 2009 Naslov: Operacije s kardinalitetima |
    |
|
|
operacije definirane na kardinalnostima su mi manje-više jasne, ali ipak se pojavilo par pitanja.
1. u jednom trenutku, na vježbama smo zapisali sljedeće:
[latex]\mathbf{c}^{\aleph_0}=(2^{\aleph_0})^{\aleph_0}=2^{\aleph_0 \cdot \aleph_0}=2^{\aleph_0}=\mathbf{c}[/latex].
muči me druga jednakost. zašto to vrijedi? ovaj primjer je, naravno, jedan od mnogih u kojima to koristimo.
pokušao sam si to objasniti na općenitom primjeru:
uzmem skupove [latex]A[/latex], [latex]B[/latex] i [latex]C[/latex]. po prethodnome bi bilo [latex](\mathit{k}(A)^{\mathit{k}(B)})^{\mathit{k}(C)} = \mathit{k}(A)^{\mathit{k}(B) \cdot \mathit{k}(C)}[/latex]. ovo bi značilo da je broj funkcija sa skupa [latex]C[/latex] u skup funkcija s [latex]B[/latex] u [latex]A[/latex] jednak broju funkcija s Kartezijevog produkta [latex]B \times C[/latex] u skup [latex]A[/latex]. a to mi je ipak prevelik zalogaj (ako je uopće jestivo :wink: )
2. isto tako, na vježbama je računato (za proizvoljni [latex]A[/latex]):
[latex]\mathit{k}(A)^{\mathit{k}(\phi)} = \mathit{k}(A)^0 = 1[/latex]. nismo li odmah mogli reći da je to 0, s obzirom da nema funkcija s praznoga skupa? :?
operacije definirane na kardinalnostima su mi manje-više jasne, ali ipak se pojavilo par pitanja.
1. u jednom trenutku, na vježbama smo zapisali sljedeće:
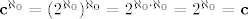 . .
muči me druga jednakost. zašto to vrijedi? ovaj primjer je, naravno, jedan od mnogih u kojima to koristimo.
pokušao sam si to objasniti na općenitom primjeru:
uzmem skupove  , ,  i i  . po prethodnome bi bilo . po prethodnome bi bilo 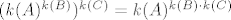 . ovo bi značilo da je broj funkcija sa skupa . ovo bi značilo da je broj funkcija sa skupa  u skup funkcija s u skup funkcija s  u u  jednak broju funkcija s Kartezijevog produkta jednak broju funkcija s Kartezijevog produkta 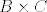 u skup u skup  . a to mi je ipak prevelik zalogaj (ako je uopće jestivo . a to mi je ipak prevelik zalogaj (ako je uopće jestivo  ) )
2. isto tako, na vježbama je računato (za proizvoljni  ): ):
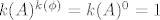 . nismo li odmah mogli reći da je to 0, s obzirom da nema funkcija s praznoga skupa? . nismo li odmah mogli reći da je to 0, s obzirom da nema funkcija s praznoga skupa? 
_________________
ima let u finish
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 20:15 pet, 24. 4. 2009 Naslov: Re: Operacije s kardinalitetima Postano: 20:15 pet, 24. 4. 2009 Naslov: Re: Operacije s kardinalitetima |
    |
|
|
[quote="rafaelm"]Ako pogledaš formalnu definiciju funkcije, onda izlazi da je [latex]\emptyset[/latex] funkcija sa praznog skupa (jedina).[/quote]
aaaaa!! :D u terminima relacija misliš? to je, pretpostavljam, zato što [latex]\forall x \in \emptyset[/latex] sve je istina (pa tako i postojanje y koji je s njim u relaciji)? je li to to?
koncentrirao sam se na onu definiciju s dva neprazna skupa, pravilom pridruživanja, bla, bla...
hvala ti.
| rafaelm (napisa): | Ako pogledaš formalnu definiciju funkcije, onda izlazi da je  funkcija sa praznog skupa (jedina). funkcija sa praznog skupa (jedina). |
aaaaa!!  u terminima relacija misliš? to je, pretpostavljam, zato što u terminima relacija misliš? to je, pretpostavljam, zato što 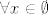 sve je istina (pa tako i postojanje y koji je s njim u relaciji)? je li to to? sve je istina (pa tako i postojanje y koji je s njim u relaciji)? je li to to?
koncentrirao sam se na onu definiciju s dva neprazna skupa, pravilom pridruživanja, bla, bla...
hvala ti.
_________________
ima let u finish
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 20:38 pet, 24. 4. 2009 Naslov: Re: Operacije s kardinalitetima Postano: 20:38 pet, 24. 4. 2009 Naslov: Re: Operacije s kardinalitetima |
    |
|
|
[quote="ma"][latex]\forall x \in \emptyset[/latex] sve je istina (pa tako i postojanje y koji je s njim u relaciji)? je li to to?[/quote]
Jep :)
A za onaj prvi dio, ja sam razmisljao o nekoj funkciji [latex]F \ : \ ^{B}(^{C}A) \rightarrow ^{B \times C}A[/latex]. Ako bih uspio naštimati da je F bijekcija, to bi dokazalo onaj identitet s kardinalnim brojevima.
[latex]f \in ^{B}(^{C}A)[/latex], tj.[latex] f \ : \ B \rightarrow ^{C}A[/latex]. Sad definiram [latex]F(f)[/latex] po točkama. [latex]F(f) \ : \ B \times C \rightarrow A[/latex], [latex](F(f))(b,c):=(f(b))(c) \in A[/latex], za [latex]b \in B[/latex], [latex]c \in C[/latex].
Mislim da bi F trebala sada biti bijekcija. Za injektivnost trivijalno raspises po definiciji [latex]F(f)=F(g)[/latex].
EDIT: Za surjektivnost: neka je [latex]g \ : \ B \times C \rightarrow A[/latex]. Sad cu naštimati [latex]f : \ B \rightarrow ^{C}A[/latex], tako da bude [latex]F(f)=g[/latex]. Neka je [latex](f(b))(c):=g(b,c)[/latex].
| ma (napisa): | 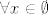 sve je istina (pa tako i postojanje y koji je s njim u relaciji)? je li to to? sve je istina (pa tako i postojanje y koji je s njim u relaciji)? je li to to? |
Jep 
A za onaj prvi dio, ja sam razmisljao o nekoj funkciji 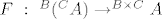 . Ako bih uspio naštimati da je F bijekcija, to bi dokazalo onaj identitet s kardinalnim brojevima. . Ako bih uspio naštimati da je F bijekcija, to bi dokazalo onaj identitet s kardinalnim brojevima.
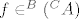 , tj. , tj.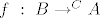 . Sad definiram . Sad definiram 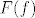 po točkama. po točkama. 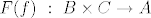 , , 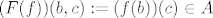 , za , za 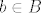 , , 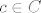 . .
Mislim da bi F trebala sada biti bijekcija. Za injektivnost trivijalno raspises po definiciji 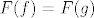 . .
EDIT: Za surjektivnost: neka je 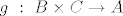 . Sad cu naštimati . Sad cu naštimati 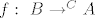 , tako da bude , tako da bude 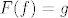 . Neka je . Neka je 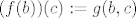 . .
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
|
| [Vrh] |
|
beba
Forumaš(ica)


Pridružen/a: 17. 08. 2006. (00:00:41)
Postovi: (41)16
Lokacija: st-ZG
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 17:30 pet, 22. 5. 2009 Naslov: Postano: 17:30 pet, 22. 5. 2009 Naslov: |
    |
|
|
1.
nek ti je S skup danih funkcija. definiraš funkciju [latex]F:\mathbb{R}\to S[/latex] s [latex]F(x)=f_x[/latex], gdje je f dana s
[latex]f_x(q) = \left\{
\begin{array}{l l}
0 & \quad \mbox{za $q<x$}\\
1 & \quad \mbox{za $q \geq x$}\\
\end{array} \right.
[/latex]
F je injekcija (to bi, naravno, trebalo pokazati- koristi se gustoća od Q u R), pa je [latex]k(S) \geq k(\mathbb{R}) = \mbox{c}[/latex]
S je podskup od [latex]^{\mathbb{Q}} \mathbb{R}[/latex], odakle je [latex]k(S) \leq \mbox{c}[/latex]. sad po CSB tm imaš da je traženi kardinalitet jednak c.
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
mutav sam. [latex]f_x[/latex] uopće nije u S :lol:
ali to lako središ- neku točku spustić u nulu. sad ću promijenit.
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[color=brown]EDIT:[/color]
[latex]f_x(q) = \left\{
\begin{array}{l l}
0 & \quad \mbox{za $q<x$ i za $q=x+1$}\\
1 & \quad \mbox{za $q \geq x$, $q \neq x+1$}\\
\end{array} \right.
[/latex]
[size=9][color=#999999]Added after 52 minutes:[/color][/size]
2.
ja bih ovako:
S={ f:Z->Z | f ne raste/pada, f nije injekcija}.
očito je k(S)<=c.
definiramo [latex]F : \langle 0,1 \rangle \to S[/latex] na sljedeći način:
za [latex]x = \overline{b_0 b_1 b_2 ...} \in \langle 0,1 \rangle[/latex] stavimo [latex]F(x) = f_x[/latex], gdje [latex]f_x[/latex] djeluje ovako:
za [latex]a \in \mathbb{Z}[/latex],
[latex]f_x(a) = \left\{
\begin{array}{l l}
b_a & \quad \mbox{ako je $a \in \mathbb{N}_0$}\\
0 & \quad \mbox{ako je $a \leq -2$}\\
-1 & \quad \mbox{ako je $a=-1$}\\
\end{array} \right.[/latex]
[latex]\forall x \in \langle 0,1 \rangle f_x[/latex] ne raste niti pada (jer je prvo 0, pa -1, pa onda samo prirodni brojevi i nula), a injekcija nije jer se 0 poprima više puta. dakle, [latex]f_x \in S[/latex].
F je injekcija jer dva različita broja iz <0,1> imaju različit decimalni zapis koji je upravo opisan funkcijom koja se dobije kao slika broja po F.
znači c=k(<0,1>) <= k(S).
po CSB teoremu, slijedi k(S)=c.
1.
nek ti je S skup danih funkcija. definiraš funkciju 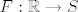 s s 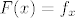 , gdje je f dana s , gdje je f dana s
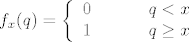
F je injekcija (to bi, naravno, trebalo pokazati- koristi se gustoća od Q u R), pa je 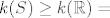
S je podskup od 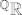 , odakle je , odakle je 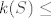 . sad po CSB tm imaš da je traženi kardinalitet jednak c. . sad po CSB tm imaš da je traženi kardinalitet jednak c.
Added after 2 minutes:
mutav sam. 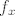 uopće nije u S uopće nije u S 
ali to lako središ- neku točku spustić u nulu. sad ću promijenit.
Added after 3 minutes:
EDIT:
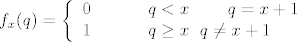
Added after 52 minutes:
2.
ja bih ovako:
S={ f:Z→Z | f ne raste/pada, f nije injekcija}.
očito je k(S)⇐c.
definiramo 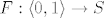 na sljedeći način: na sljedeći način:
za 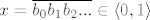 stavimo stavimo 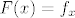 , gdje , gdje 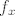 djeluje ovako: djeluje ovako:
za 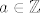 , ,
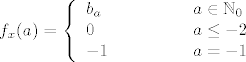
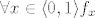 ne raste niti pada (jer je prvo 0, pa -1, pa onda samo prirodni brojevi i nula), a injekcija nije jer se 0 poprima više puta. dakle, ne raste niti pada (jer je prvo 0, pa -1, pa onda samo prirodni brojevi i nula), a injekcija nije jer se 0 poprima više puta. dakle, 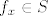 . .
F je injekcija jer dva različita broja iz <0,1> imaju različit decimalni zapis koji je upravo opisan funkcijom koja se dobije kao slika broja po F.
znači c=k(<0,1>) ⇐ k(S).
po CSB teoremu, slijedi k(S)=c.
_________________
ima let u finish
|
|
| [Vrh] |
|
beba
Forumaš(ica)


Pridružen/a: 17. 08. 2006. (00:00:41)
Postovi: (41)16
Lokacija: st-ZG
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 23:15 sub, 27. 6. 2009 Naslov: Postano: 23:15 sub, 27. 6. 2009 Naslov: |
    |
|
|
[quote="beba"]kardinalnost realnih redova cija je suma negativna?[/quote]
Označimo s S traženi skup. Jer je S podskup R^N onda k(S)<=c.
Sad uzmimo f:R->S
definiranu sa:
f(x)=(x,-x,-1,0,0,0....)
f je očito injekcija, pa je c<=k(S).
| beba (napisa): | | kardinalnost realnih redova cija je suma negativna? |
Označimo s S traženi skup. Jer je S podskup R^N onda k(S)⇐c.
Sad uzmimo f:R→S
definiranu sa:
f(x)=(x,-x,-1,0,0,0....)
f je očito injekcija, pa je c⇐k(S).
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 0:01 ned, 28. 6. 2009 Naslov: Postano: 0:01 ned, 28. 6. 2009 Naslov: |
    |
|
|
evo ja ću ti prvi.
[latex]S=\{f \in ^{\mathbb{N}}\mathbb{N} | f $ strogo monoton$\}[/latex].
[latex]k(S) \leq c[/latex] iz očitih razloga.
definiraš [latex]F: \mathbb{R} \rightarrow S[/latex] na sljedeći način (dat ću ilustraciju):
[latex]F(3)=(0,13,220,2220,22220,222220,\dots)[/latex]
[latex]F(-7)=(1,17,220,2220,22220,222220,\dots)[/latex]
[latex]F(-24.75)=(1,12,114,2227,22225,222220,2222220,\dots)[/latex]
[latex]F(6708.6708)=(0,16,117,1110,11118,222226,2222227,22222220,222222228,2222222220,\dots)[/latex]
[latex]F(-\pi)=(1,13,221,2224,22221,222225,\dots)[/latex]
nadam se da je jasno. prvi član niza ukazuje na predznak, dalje idu jedinice (u svakom idućem članu po jedna više) iza kojih su znamenke cjelobrojnog dijela argumenta, nakon toga idu dvojke (također sve više i više) s decimalama iza sebe.
lako se vidi da je rng(F) u S, kao i da je F injekcija. za svaki niz tog tipa točno znaš od kojeg broja dolazi.
i sad CSB. odgovor je c.
p.s. vrlo vjerojatno postoji i elegantniji način, ali ovo mi se čini sasvim legitimno.
evo ja ću ti prvi.
 . .
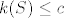 iz očitih razloga. iz očitih razloga.
definiraš 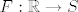 na sljedeći način (dat ću ilustraciju): na sljedeći način (dat ću ilustraciju):
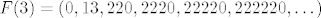
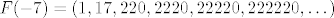
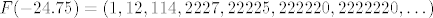
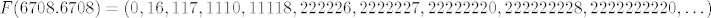
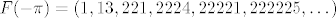
nadam se da je jasno. prvi član niza ukazuje na predznak, dalje idu jedinice (u svakom idućem članu po jedna više) iza kojih su znamenke cjelobrojnog dijela argumenta, nakon toga idu dvojke (također sve više i više) s decimalama iza sebe.
lako se vidi da je rng(F) u S, kao i da je F injekcija. za svaki niz tog tipa točno znaš od kojeg broja dolazi.
i sad CSB. odgovor je c.
p.s. vrlo vjerojatno postoji i elegantniji način, ali ovo mi se čini sasvim legitimno.
_________________
ima let u finish
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 0:38 ned, 28. 6. 2009 Naslov: Postano: 0:38 ned, 28. 6. 2009 Naslov: |
    |
|
|
@ma: fino :)
Evo još jedan način. Ako je [latex](a_n)_{n\in \mathbb{N}}[/latex] strogo rastući niz priridnih brojeva, onda je [latex] (a_{n+1}-a_n)_{n\in \mathbb{N}}[/latex] niz prirodnih brojeva (gledamo samo razlike susjednh članova), i to pridruživanje je očito bijektivno. A svih nizova prirodnih brojeva ima [latex]c[/latex].
Edit: mala modifikacija: rastućem nizu [latex](a_1,a_2,\ldots)[/latex] pridružimo [latex](a_1,a2-a1,a3-a2,\ldots)[/latex]
Edit2: sjetih se da je na ovom kolegiju nula prirodan broj. Dakle, kodomena je skup svih nizova prirodnih brojeva koji samo na prvom mjestu mogu imati nulu. Lako je viditi da i takvih ima [latex] c[/latex].
@ma: fino 
Evo još jedan način. Ako je 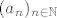 strogo rastući niz priridnih brojeva, onda je strogo rastući niz priridnih brojeva, onda je 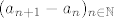 niz prirodnih brojeva (gledamo samo razlike susjednh članova), i to pridruživanje je očito bijektivno. A svih nizova prirodnih brojeva ima niz prirodnih brojeva (gledamo samo razlike susjednh članova), i to pridruživanje je očito bijektivno. A svih nizova prirodnih brojeva ima  . .
Edit: mala modifikacija: rastućem nizu 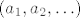 pridružimo pridružimo 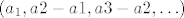
Edit2: sjetih se da je na ovom kolegiju nula prirodan broj. Dakle, kodomena je skup svih nizova prirodnih brojeva koji samo na prvom mjestu mogu imati nulu. Lako je viditi da i takvih ima  . .
|
|
| [Vrh] |
|
artapoelk
Forumaš(ica)
Pridružen/a: 09. 09. 2007. (17:06:50)
Postovi: (9)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
|















