Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

zadaća 5
WWW:
Idite na Prethodno  1, 2
Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
ddduuu
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
Sarma = la pohva - posuda
4 = 20 - 16
PostPostano: 21:55 ned, 28. 6. 2009    Naslov: Citirajte i odgovorite
jel ima ko ideju za 3.14 pod e i f:)
jel ima ko ideju za 3.14 pod e i fSmile


[Vrh]
Korisnički profil Pošaljite privatnu poruku
ivek imudaš
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 13. 11. 2007. (18:41:02)
Postovi: (67)16
Spol: muško
Sarma = la pohva - posuda
12 = 14 - 2
PostPostano: 22:44 ned, 28. 6. 2009    Naslov: Citirajte i odgovorite
[quote="ddduuu"]jel ima ko ideju za 3.14 pod e i f:)[/quote]

f) cauchy
dobijes
(n^2)^(1/n) u nazivniku sto ide u 1
brojnik ln(n) ide u beskonacno
tj limes je nula pa konvergira

e) modul(sin1/n*sh1/n*cosn)<=sin1/n*sh1/n
ovo sa desne starne je uvijek pozitivno mos provjerit
onda sa granicnim kriterijem i 1/n^2 trazis limes u beskonacno
tj lim (sin1/n*sh1/n)/(1/n^2) sto je ekvivalentno sa lim(u 0) (sint)/t(sht)/t a
ta dva imas u tablici i ti su 1
red sa opcim clanom 1/n^2 je konvergentan pa konvergira i red sa clanovima sin1/n*sh1/n pa po usporednom kriteriju konvergira i pocetni red
ddduuu (napisa):
jel ima ko ideju za 3.14 pod e i fSmile


f) cauchy
dobijes
(n^2)^(1/n) u nazivniku sto ide u 1
brojnik ln(n) ide u beskonacno
tj limes je nula pa konvergira

e) modul(sin1/n*sh1/n*cosn)⇐sin1/n*sh1/n
ovo sa desne starne je uvijek pozitivno mos provjerit
onda sa granicnim kriterijem i 1/n^2 trazis limes u beskonacno
tj lim (sin1/n*sh1/n)/(1/n^2) sto je ekvivalentno sa lim(u 0) (sint)/t(sht)/t a
ta dva imas u tablici i ti su 1
red sa opcim clanom 1/n^2 je konvergentan pa konvergira i red sa clanovima sin1/n*sh1/n pa po usporednom kriteriju konvergira i pocetni red


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Gino
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Sarma = la pohva - posuda
-29 = 108 - 137
Lokacija: Pula
PostPostano: 22:57 ned, 28. 6. 2009    Naslov: Citirajte i odgovorite
u zadatku 3.33.e mi na kraju treba
[latex]\displaystyle \int \frac{\ln (1-x)}{x} dx[/latex] :?: :?:

ili se moze rjesit i bez toga :?:
u zadatku 3.33.e mi na kraju treba
Question Question

ili se moze rjesit i bez toga Question



_________________
Mario Berljafa
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Grga
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: muško
Sarma = la pohva - posuda
99 = 124 - 25
PostPostano: 12:48 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
[quote="Gino"]u zadatku 3.33.e mi na kraju treba
[latex]\displaystyle \int \frac{\ln (1-x)}{x} dx[/latex] :?: :?:

ili se moze rjesit i bez toga :?:[/quote]

Niti se to moze lijepo integrirati, niti mi pada na pamet drugi nacin kako to rijesiti. I mene bi zanimalo ako netko zna jer sad se svakih 20 minuta vracam na pokusaje da to rijesim umjesto da ucim sto bih trebao :P
Gino (napisa):
u zadatku 3.33.e mi na kraju treba
Question Question

ili se moze rjesit i bez toga Question


Niti se to moze lijepo integrirati, niti mi pada na pamet drugi nacin kako to rijesiti. I mene bi zanimalo ako netko zna jer sad se svakih 20 minuta vracam na pokusaje da to rijesim umjesto da ucim sto bih trebao Razz



_________________
Bri
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Mr.Doe
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
Sarma = la pohva - posuda
20 = 50 - 30
PostPostano: 14:40 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
[quote="Gino"]u zadatku 3.33.e mi na kraju treba
[latex]\displaystyle \int \frac{\ln (1-x)}{x} dx[/latex] :?: :?:

ili se moze rjesit i bez toga :?:[/quote]

Razvi [latex]\operatorname{ln}(1-x)[/latex] u red :shock: !
Dobit ces [latex]\sum_{n=1}^{\infty}(-1)^{n-1}\frac{1}{n^2}+C[/latex] nakon integracije.

Btw. nemam pojma o kojem je zadatku rijec, niti koji je kontekst.
Gino (napisa):
u zadatku 3.33.e mi na kraju treba
Question Question

ili se moze rjesit i bez toga Question


Razvi u red Shocked !
Dobit ces nakon integracije.

Btw. nemam pojma o kojem je zadatku rijec, niti koji je kontekst.


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Grga
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: muško
Sarma = la pohva - posuda
99 = 124 - 25
PostPostano: 15:09 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
[quote="Mr.Doe"][quote="Gino"]u zadatku 3.33.e mi na kraju treba
[latex]\displaystyle \int \frac{\ln (1-x)}{x} dx[/latex] :?: :?:

ili se moze rjesit i bez toga :?:[/quote]

Razvi [latex]\operatorname{ln}(1-x)[/latex] u red :shock: !
Dobit ces [latex]\sum_{n=1}^{\infty}(-1)^{n-1}\frac{1}{n^2}+C[/latex] nakon integracije.

Btw. nemam pojma o kojem je zadatku rijec, niti koji je kontekst.[/quote]

Ma u tom i je problem... Znamo da je integral Taylorovog reda takav (makar ti fali x^n), a to se poklapa s redom kojeg zelimo recunati, no mi trebamo izraz za taj integral u koji mozemo uvrstiti -1/3 da dobijemo sumu reda koja se trazi
Mr.Doe (napisa):
Gino (napisa):
u zadatku 3.33.e mi na kraju treba
Question Question

ili se moze rjesit i bez toga Question


Razvi u red Shocked !
Dobit ces nakon integracije.

Btw. nemam pojma o kojem je zadatku rijec, niti koji je kontekst.


Ma u tom i je problem... Znamo da je integral Taylorovog reda takav (makar ti fali x^n), a to se poklapa s redom kojeg zelimo recunati, no mi trebamo izraz za taj integral u koji mozemo uvrstiti -1/3 da dobijemo sumu reda koja se trazi



_________________
Bri
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Mr.Doe
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
Sarma = la pohva - posuda
20 = 50 - 30
PostPostano: 15:55 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
Ok, hvala na opaski, rekao sam da mi nije jasan kontekst zadatka. Moze netko napisati cijeli zadatak, mozda se moze rijesiti na drugi nacin...
Ok, hvala na opaski, rekao sam da mi nije jasan kontekst zadatka. Moze netko napisati cijeli zadatak, mozda se moze rijesiti na drugi nacin...


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Gino
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Sarma = la pohva - posuda
-29 = 108 - 137
Lokacija: Pula
PostPostano: 16:07 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
sad me vise zanima onaj koji nisam znao na kolokviju
[latex]\displaystyle \sum \frac{1}{(4n)!}[/latex]
sad me vise zanima onaj koji nisam znao na kolokviju



_________________
Mario Berljafa
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Mr.Doe
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
Sarma = la pohva - posuda
20 = 50 - 30
PostPostano: 16:17 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
[latex]\displaystyle \sum_{n=0}^{\infty}\frac{1}{(4n)!}=\frac{e-e^{-1}}{2}-\frac{e^i-e^{-i}}{2}[/latex] :shock:
Shocked


[Vrh]
Korisnički profil Pošaljite privatnu poruku
Milojko
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: kućni ljubimac
Sarma = la pohva - posuda
17 = 68 - 51
Lokacija: Hilbertov hotel
PostPostano: 16:22 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
a kak da ja ovak mutav dođem do toga??
de malo pojasni postupak
a kak da ja ovak mutav dođem do toga??
de malo pojasni postupak



_________________
Sedam je prost broj Smile

Bolonja je smeće i to pod hitno treba mijenjat
[Vrh]
Korisnički profil Pošaljite privatnu poruku MSNM
Mr.Doe
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
Sarma = la pohva - posuda
20 = 50 - 30
PostPostano: 16:35 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
Prvo primjedba: zezuo sam oduzimanje, treba biti zbrajanje i zaboravio na kraju sve podijeliti sa 2! :roll:

Prvo pogledas red, i kazes (sam sebi, da ne ometas ljude na kolokviju):"Pa, ovo izgleda kao red od e, samo sto ima ona cetvorka". Pa onda malo mislis, i kazes idem ja prvo nastelat da je dolje dvojka, pa onda jos malo razmisljas, pa kazes (sam sebi), znam red od e, a brijem da bi znao i od e^{-1}, pa ajdem ih onda da ih zbrojim (jel je to lakse od oduzimanja), pa dobijem
[latex]\displaystyle \sum_{n=0}^{\infty}\frac{2}{(2n)!}[/latex],
zatim kazes (sam sebi, potiho):"koji sam ja car, e ziher cu rijesiti zadatak!"
E, sada kad bih uspio jos nekak, slicno zbrojiti e^{nesta} sa e^{nesta drugo}, onda bi ziher bio faca, pa malo razmisljas i kazes mogao bi probati pogledat e^{i} i e^{-i}, ( jer su [latex]1,i,\pi,e[/latex] jedini brojevi u matematici koje moram pamtiti,pa onda redom probavas ), pa to zbroji i dobijes
[latex]\displaystyle \sum_{n=0}^{\infty}\frac{2(-1)^n}{(2n)!}[/latex],
sada otprilike pocinjes razmisljati kak si velika faca, i kak ces rasturiti usmeni kod Guljasa(!), pa kazes ajde da ja sve to zbrojim (jer ponovno lakse je zbrajati nego oduzimati), pa dobijes
[latex]\displaystyle \sum_{n=0}^{\infty}\frac{2}{(4n)!}[/latex],
pa zatim jos podijelis sve sa 2 (jer bio inace kao ja zgubio bodove), i kazes:

[latex]\frac{e+e^{-1}+e^{i}+e^{-i}}{4}=\sum_{n=0}^{\infty}\frac{1}{(4n)!}[/latex]

i napises ispod poruku asistentima:"Daj sljedeci put malo tezi zadatak

:roll: "

Primjedba: zadrzavam pravo da sam negdje pogrijesio.
Prvo primjedba: zezuo sam oduzimanje, treba biti zbrajanje i zaboravio na kraju sve podijeliti sa 2! Rolling Eyes

Prvo pogledas red, i kazes (sam sebi, da ne ometas ljude na kolokviju):"Pa, ovo izgleda kao red od e, samo sto ima ona cetvorka". Pa onda malo mislis, i kazes idem ja prvo nastelat da je dolje dvojka, pa onda jos malo razmisljas, pa kazes (sam sebi), znam red od e, a brijem da bi znao i od e^{-1}, pa ajdem ih onda da ih zbrojim (jel je to lakse od oduzimanja), pa dobijem
,
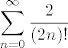zatim kazes (sam sebi, potiho):"koji sam ja car, e ziher cu rijesiti zadatak!"
E, sada kad bih uspio jos nekak, slicno zbrojiti e^{nesta} sa e^{nesta drugo}, onda bi ziher bio faca, pa malo razmisljas i kazes mogao bi probati pogledat e^{i} i e^{-i}, ( jer su 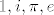jedini brojevi u matematici koje moram pamtiti,pa onda redom probavas ), pa to zbroji i dobijes
,
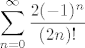sada otprilike pocinjes razmisljati kak si velika faca, i kak ces rasturiti usmeni kod Guljasa(!), pa kazes ajde da ja sve to zbrojim (jer ponovno lakse je zbrajati nego oduzimati), pa dobijes
,
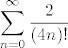pa zatim jos podijelis sve sa 2 (jer bio inace kao ja zgubio bodove), i kazes:



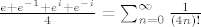
i napises ispod poruku asistentima:"Daj sljedeci put malo tezi zadatak

Rolling Eyes "

Primjedba: zadrzavam pravo da sam negdje pogrijesio.




Zadnja promjena: Mr.Doe; 16:46 pon, 29. 6. 2009; ukupno mijenjano 1 put.
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Thor
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 04. 2009. (10:57:50)
Postovi: (15)16
Sarma = la pohva - posuda
1 = 1 - 0
PostPostano: 16:41 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
E ja sam ga ovako riješio ali očito je krivo samo neznam bas gdje
[latex](4n)!=4n(4n-4)...4=4^nn![/latex]
i onda samo napravio red
[latex] x^n/n![/latex] gdje je x=1/4 tj funkciju [latex]e^x[/latex] gdje je x=1/4
pa sam dobio rješenje
[latex]e^(1/4)[/latex]
E ja sam ga ovako riješio ali očito je krivo samo neznam bas gdje

i onda samo napravio red
gdje je x=1/4 tj funkciju gdje je x=1/4
pa sam dobio rješenje



_________________
Devil's playground
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Mr.Doe
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 01. 2005. (21:20:57)
Postovi: (21A)16
Sarma = la pohva - posuda
20 = 50 - 30
PostPostano: 16:47 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
Ovdje [quote="Thor"] očito je krivo samo neznam bas gdje
[latex](4n)!=4n(4n-4)...4=4^nn![/latex]
[/quote]

[latex](4n)!=4n(4n-1)\dots 1[/latex]
Ovdje
Thor (napisa):
očito je krivo samo neznam bas gdje





[Vrh]
Korisnički profil Pošaljite privatnu poruku
Thor
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 24. 04. 2009. (10:57:50)
Postovi: (15)16
Sarma = la pohva - posuda
1 = 1 - 0
PostPostano: 16:50 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
naravno samo ja mogu tako nešto zaključit :( :?
naravno samo ja mogu tako nešto zaključit Sad Confused



_________________
Devil's playground
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Grga
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 23. 12. 2004. (23:05:23)
Postovi: (280)16
Spol: muško
Sarma = la pohva - posuda
99 = 124 - 25
PostPostano: 17:33 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
[quote="Thor"]naravno samo ja mogu tako nešto zaključit :( :?[/quote]
Meni se isto dogodilo jednom prilikom, bas za (4n)! :oops:

@Mr.Doe
Treba izracunati
[latex]\displaystyle \sum_{n=1}^\infty \frac{(-1)^n}{n^2 3^n}[/latex]
Thor (napisa):
naravno samo ja mogu tako nešto zaključit Sad Confused

Meni se isto dogodilo jednom prilikom, bas za (4n)! Embarassed

@Mr.Doe
Treba izracunati



_________________
Bri
[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail
Gino
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 11. 09. 2008. (10:54:06)
Postovi: (370)16
Sarma = la pohva - posuda
-29 = 108 - 137
Lokacija: Pula
PostPostano: 21:12 pon, 29. 6. 2009    Naslov: Citirajte i odgovorite
[quote="Mr.Doe"]Prvo pogledas red, i kazes (sam sebi, da ne ometas ljude na kolokviju):"Pa, ovo izgleda kao red od e, samo sto ima ona cetvorka".[/quote]

dakle bio sam na dobrom putu :lol: :lol:
Mr.Doe (napisa):
Prvo pogledas red, i kazes (sam sebi, da ne ometas ljude na kolokviju):"Pa, ovo izgleda kao red od e, samo sto ima ona cetvorka".


dakle bio sam na dobrom putu Laughing Laughing



_________________
Mario Berljafa
[Vrh]
Korisnički profil Pošaljite privatnu poruku
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2 Vremenska zona: GMT + 01:00.
Idite na Prethodno  1, 2
Stranica 2 / 2.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan