| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Sylph
Forumaš(ica)
Pridružen/a: 02. 02. 2008. (12:40:16)
Postovi: (B)16
|
 Postano: 20:18 ned, 7. 9. 2008 Naslov: Taylorov teorem Postano: 20:18 ned, 7. 9. 2008 Naslov: Taylorov teorem |
    |
|
|
imam jednu nejasnocu, koja je mozda ocita, al ja nikak da skuzim:(
dakle, u dokazu Taylorovog teorema pred kraj, kad vec pokazemo f kao sumu odgovarajuceg reda, ali koeficijenti su nam dani kao integral po kruznici gama ro. i sad se veli da je f(zeta)/zeta^(n+1) holomorfna na probusenom krugu oko 0 radijusa r, i kruznica gama ro je u tom istom krugu homotopna kruznici gama0, pa po Cauchyjevom teoremu slijedi da su integrali po tim kruznicama jednaki. E sad, moje pitanje je di smo tu tocno koristili Cauchyjev teorem, tj zasto po njemu to slijedi.
nadam se da je dovoljno razumljivo kaj me muci da netko moze odgovorit:)
zahvalna sam na odgovoru:)
imam jednu nejasnocu, koja je mozda ocita, al ja nikak da skuzim:(
dakle, u dokazu Taylorovog teorema pred kraj, kad vec pokazemo f kao sumu odgovarajuceg reda, ali koeficijenti su nam dani kao integral po kruznici gama ro. i sad se veli da je f(zeta)/zeta^(n+1) holomorfna na probusenom krugu oko 0 radijusa r, i kruznica gama ro je u tom istom krugu homotopna kruznici gama0, pa po Cauchyjevom teoremu slijedi da su integrali po tim kruznicama jednaki. E sad, moje pitanje je di smo tu tocno koristili Cauchyjev teorem, tj zasto po njemu to slijedi.
nadam se da je dovoljno razumljivo kaj me muci da netko moze odgovorit:)
zahvalna sam na odgovoru:)
|
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 23:17 pon, 21. 9. 2009 Naslov: Postano: 23:17 pon, 21. 9. 2009 Naslov: |
    |
|
|
Ne znam na sto tocno mislis, evo dokaza koji sam ja naucio na MMFu (na fizici, jer sam fizicar) a koji se tice Taylorovog teorema:
Dakle, ako je f(z) analiticka unutra kruga C sa sredistem u a, tada [latex]\forall z\in\mathbb{C}[/latex] vrijedi:
[latex]f(z)=f(a)+f'(a)(z-a)+\frac{f''(a)}{2!}}(z-a)^2+\ldots[/latex]
Cauchy integralna formula nam kaze sljedece:
[latex]f(z)=\frac{1}{2\pi i}\oint\limits_{C_1} \frac{f(\zeta)}{\zeta-z}\mathrm{d}\zeta[/latex]
Krug C_1 je sadrzan unutar kruga C i sadrzi tocke a i z (srediste kruga C_1 je u tocki a) i pozitivno je orjentiran (kao i krug C). Sad iz Cauchy integralne formule vidimo koji nam je problematicni dio i njega razvijamo (to mozemo). Dobijemo sljedece:
[latex]\frac{1}{\zeta-z}=\frac{1}{(\zeta-a)-(z-a)}=\ldots=\sum\limits_{k=0}^{+\infty}\frac{(z-a)^k}{(\zeta-a)^{k+1}}[/latex]
Sad taj rezultat ubacimo gore u C.I.F. i dobijemo:
[latex]f(z)=\frac{1}{2\pi i}\oint\limits_{C_1}\sum\limits_{k=0}^{+\infty}\frac{(z-a)^k}{(\zeta-a)^{k+1}}f(\zeta)\mathtm{d}\zeta[/latex]
odnosno
[latex]f(z)=\sum\limits_{k=0}^{+\infty}(z-a)^k\cdot\oint\limits_{C_1}\frac{f(\zeta)}{(\zeta-a)^{k+1}}\mathrm{d}\zeta[/latex]
No, ovaj integral desno prepoznajemo kao k-tu derivaciju u tocki a u Cauchyevoj integralnoj formuli, pa stoga mozemo pisati:
[latex]f(z)=\sum\limits_{k=0}^{+\infty}\frac{f^{(n)}(a)}{k!}(z-a)^k[/latex]
Ono sto je bitno jest da nije Cauchyev integralni teorem taj koji ti daje da prelazis sa kruznice na kruznicu, vec ti to garantira sama analiticnost prostora. Takodjer, da bismo znali vrijednost neke funkcije u tocki z_0, moramo znati vrijednost [b]bilo kojeg[/b] zatvorenog puta oko z_0. Ta konkretna vrijednost na rubu [b]potpuno[/b] odredjuje vrijednost unutar kruga.Sve dok se god nalazimo unutar analiticnosti, odnosno unutar podrucja S na kojem je (pretpostavka) funkcija f(z) analiticna.
Ne znam na sto tocno mislis, evo dokaza koji sam ja naucio na MMFu (na fizici, jer sam fizicar) a koji se tice Taylorovog teorema:
Dakle, ako je f(z) analiticka unutra kruga C sa sredistem u a, tada 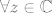 vrijedi: vrijedi:
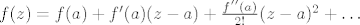
Cauchy integralna formula nam kaze sljedece:
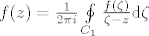
Krug C_1 je sadrzan unutar kruga C i sadrzi tocke a i z (srediste kruga C_1 je u tocki a) i pozitivno je orjentiran (kao i krug C). Sad iz Cauchy integralne formule vidimo koji nam je problematicni dio i njega razvijamo (to mozemo). Dobijemo sljedece:
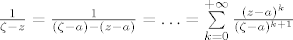
Sad taj rezultat ubacimo gore u C.I.F. i dobijemo:
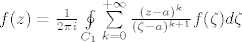
odnosno
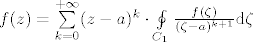
No, ovaj integral desno prepoznajemo kao k-tu derivaciju u tocki a u Cauchyevoj integralnoj formuli, pa stoga mozemo pisati:

Ono sto je bitno jest da nije Cauchyev integralni teorem taj koji ti daje da prelazis sa kruznice na kruznicu, vec ti to garantira sama analiticnost prostora. Takodjer, da bismo znali vrijednost neke funkcije u tocki z_0, moramo znati vrijednost bilo kojeg zatvorenog puta oko z_0. Ta konkretna vrijednost na rubu potpuno odredjuje vrijednost unutar kruga.Sve dok se god nalazimo unutar analiticnosti, odnosno unutar podrucja S na kojem je (pretpostavka) funkcija f(z) analiticna.
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 6:54 uto, 22. 9. 2009 Naslov: Postano: 6:54 uto, 22. 9. 2009 Naslov: |
    |
|
|
[quote="HijenA"]
Dakle, ako je f(z) analiticka unutra kruga C sa sredistem u a, tada [latex]\forall z\in\mathbb{C}[/latex] vrijedi:
[latex]f(z)=f(a)+f'(a)(z-a)+\frac{f''(a)}{2!}}(z-a)^2+\ldots[/latex]
[/quote]
:lol: :lol: Ti dokazuješ Taylorov tm, a u prvom koraku koristiš ono što on kaže :D
[quote]E sad, moje pitanje je di smo tu tocno koristili Cauchyjev teorem, tj zasto po njemu to slijedi. [/quote]
Slijedi po njemu jer on kaže da je po svakom zatv nulhom putu integral nula. To je ekvivalentno tome da je integral po međusobnom homotopnim putevima, sa istim početkom i krajem, jednake vrijednosti. Homotopija između ta dva puta je slična ko u dokazu korolara 34.6. (da bi se do nje došlo, trebaju još ona linija od jedne do druge kružnice, onda su tu počeci i krajevi) :D
| HijenA (napisa): |
Dakle, ako je f(z) analiticka unutra kruga C sa sredistem u a, tada 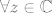 vrijedi: vrijedi:
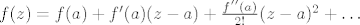
|
  Ti dokazuješ Taylorov tm, a u prvom koraku koristiš ono što on kaže Ti dokazuješ Taylorov tm, a u prvom koraku koristiš ono što on kaže 
| Citat: | | E sad, moje pitanje je di smo tu tocno koristili Cauchyjev teorem, tj zasto po njemu to slijedi. |
Slijedi po njemu jer on kaže da je po svakom zatv nulhom putu integral nula. To je ekvivalentno tome da je integral po međusobnom homotopnim putevima, sa istim početkom i krajem, jednake vrijednosti. Homotopija između ta dva puta je slična ko u dokazu korolara 34.6. (da bi se do nje došlo, trebaju još ona linija od jedne do druge kružnice, onda su tu počeci i krajevi) 
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
HijenA
Forumaš(ica)

Pridružen/a: 23. 01. 2004. (16:46:04)
Postovi: (3D2)16
Spol: 
Lokacija: Prazan skup ;-)
|
 Postano: 10:53 uto, 22. 9. 2009 Naslov: Postano: 10:53 uto, 22. 9. 2009 Naslov: |
    |
|
|
[quote="Luuka"][quote="HijenA"]
Dakle, ako je f(z) analiticka unutra kruga C sa sredistem u a, tada [latex]\forall z\in\mathbb{C}[/latex] vrijedi:
[latex]f(z)=f(a)+f'(a)(z-a)+\frac{f''(a)}{2!}}(z-a)^2+\ldots[/latex]
[/quote]
:lol: :lol: Ti dokazuješ Taylorov tm, a u prvom koraku koristiš ono što on kaže :D[/quote]
nope, samo sam izrekao tvrdnju :-P kasnije smo samo koristili mogucnost razvoja u red potencija, sto mozemo neovisno o postojanju Taylorovog reda.
[quote]
[quote]E sad, moje pitanje je di smo tu tocno koristili Cauchyjev teorem, tj zasto po njemu to slijedi. [/quote]
Slijedi po njemu jer on kaže da je po svakom zatv nulhom putu integral nula. To je ekvivalentno tome da je integral po međusobnom homotopnim putevima, sa istim početkom i krajem, jednake vrijednosti. Homotopija između ta dva puta je slična ko u dokazu korolara 34.6. (da bi se do nje došlo, trebaju još ona linija od jedne do druge kružnice, onda su tu počeci i krajevi) :D[/quote][/quote]
da nisam bolestan, shvatio bi sto se pita :-) ja sam cijelo vrijeme u glavi imao Cauchyevu integralnu formulu, nisam se ni sjetio Cauchyevog teorema, odnosno Cauchy-Goursadovog teorema (prosirenje ovog prvog).
| Luuka (napisa): | | HijenA (napisa): |
Dakle, ako je f(z) analiticka unutra kruga C sa sredistem u a, tada 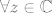 vrijedi: vrijedi:
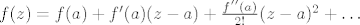
|
  Ti dokazuješ Taylorov tm, a u prvom koraku koristiš ono što on kaže Ti dokazuješ Taylorov tm, a u prvom koraku koristiš ono što on kaže  |
nope, samo sam izrekao tvrdnju  kasnije smo samo koristili mogucnost razvoja u red potencija, sto mozemo neovisno o postojanju Taylorovog reda. kasnije smo samo koristili mogucnost razvoja u red potencija, sto mozemo neovisno o postojanju Taylorovog reda.
| Citat: |
| Citat: | | E sad, moje pitanje je di smo tu tocno koristili Cauchyjev teorem, tj zasto po njemu to slijedi. |
Slijedi po njemu jer on kaže da je po svakom zatv nulhom putu integral nula. To je ekvivalentno tome da je integral po međusobnom homotopnim putevima, sa istim početkom i krajem, jednake vrijednosti. Homotopija između ta dva puta je slična ko u dokazu korolara 34.6. (da bi se do nje došlo, trebaju još ona linija od jedne do druge kružnice, onda su tu počeci i krajevi)  |
[/quote]
da nisam bolestan, shvatio bi sto se pita  ja sam cijelo vrijeme u glavi imao Cauchyevu integralnu formulu, nisam se ni sjetio Cauchyevog teorema, odnosno Cauchy-Goursadovog teorema (prosirenje ovog prvog). ja sam cijelo vrijeme u glavi imao Cauchyevu integralnu formulu, nisam se ni sjetio Cauchyevog teorema, odnosno Cauchy-Goursadovog teorema (prosirenje ovog prvog).
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
|








