|
ne radi se o mojim demonstraturama, al me demosica zamolila da vam napisem rjesenje, jer ona nije jos dosla doma
to su te price :lol: :lol:
dakle zadatak je bio ovako nesto
ako je [latex]\{b_1,b_2,...,b_n\}[/latex] baza za [latex]V[/latex] dokazite da je [latex]\displaystyle\{\sum_{i=1}^n\alpha_i b_i,b_2,b_3,...,b_n\}[/latex] baza za [latex]V[/latex] akko je [latex]\alpha_1\neq 0[/latex]
dokazimo da ako je [latex]\alpha_1\neq 0[/latex] da je onda [latex]\displaystyle\{\sum_{i=1}^n\alpha_i b_i,b_2,b_3,...,b_n\}[/latex] baza za [latex]V[/latex]
mora se samo dokazat da je [latex]\displaystyle\{\sum_{i=1}^n\alpha_i b_i,b_2,b_3,...,b_n\}[/latex] linearno nezavisno
pretpostavimo suprotno:
[latex]\alpha_1\neq 0[/latex] i [latex]\displaystyle\{\sum_{i=1}^n\alpha_i b_i,b_2,b_3,...,b_n\}[/latex] nije linearno nezavisno, sto znaci da postoje skalari [latex]\beta_1,...,\beta_n[/latex] koji nisu svi [latex]0[/latex] i vrijedi [latex]\displaystyle\beta_1\sum_{i=1}^n\alpha_ib_i +\sum_{j=2}^n\beta_jb_j=0[/latex]
sad to malo "grupiramo" i dobimo:
[latex]\displaystyle\beta_1\alpha_1b_1+\sum_{i=2}^n\left(\beta_1 \alpha_i +\beta_i\right) b_i=0[/latex]
no kako je [latex]\{b_1,b_2,...,b_n\}[/latex] baza slijedi da su svi ovi skalari jednaki [latex]0[/latex]
sad se sjetimo pretpostavke bar za jedan [latex]j[/latex] je[latex]\beta_j\neq 0[/latex]
ako je to za [latex]j=1[/latex] , kako je [latex]\beta_1\alpha_1=0 \wedge \beta_1\neq 0[/latex] to je [latex]\alpha_1=0[/latex] no to je kontradikcija sa pretpostavkom da je [latex]\alpha_1\neq 0[/latex]
neka je sad [latex]\beta_j\neq 0 \wedge j\neq 1[/latex], kako je
[latex]\beta_1\alpha_j+\beta_j=0 \wedge \beta_j\neq0[/latex] to je [latex]\beta_1\alpha_j\neq 0[/latex] pa je posebno [latex] \beta_1\neq 0 [/latex] no kako je [latex]\beta_1\alpha_1=0[/latex] slijedi da je [latex]\alpha_1=0[/latex] sto je kontradikcija, i time je dokazan ovaj smjer
pokazimo sad da ako je [latex]\displaystyle\{\sum_{i=1}^n\alpha_i b_i,b_2,b_3,...,b_n\}[/latex] baza da je onda [latex]\alpha_1\neq 0[/latex]
neznam zasto, al opet cu pretpostavit suprotno, neka je ono baza i neka je [latex]\alpha_1=0[/latex]
sad, jer je ono baza, onda je i linearno nezavisno pa je [latex]\displaystyle\beta_1\sum_{i=1}^n\alpha_ib_i +\sum_{j=2}^n\beta_jb_j=0[/latex] samo kada su svi [latex]\beta_i=0[/latex], pogledajmo je li to zaista tako
grupiramo ono malo i uvazimo da je [latex]\alpha_1=0[/latex]
sada dobivamo:
[latex]\displaystyle\sum_{i=2}^n\left(\beta_1\alpha_i+\beta_i\right)b_i=0[/latex]
sad, ili su mi svi [latex]\alpha_i=0[/latex] za [latex]i=2,...,n[/latex], ili bar jedan nije
ako su svi [latex]0[/latex] ondauzme [latex]\beta_1=1[/latex] i imam kontradikciju, ako bar jedan nije, npr ako je [latex]\alpha_j\neq 0[/latex]za neki [latex]j\ge 2[/latex] onda stavim da je [latex]\beta_1=1 \wedge \beta_j=-\alpha_j[/latex] i opet imam kontradikciju
time je tvrdnja dokazana
nadam se da je ok rijeseno, i da ce pomoc
... mozda se moze i krace, al... eto... ja sam ovako :D
ne radi se o mojim demonstraturama, al me demosica zamolila da vam napisem rjesenje, jer ona nije jos dosla doma
to su te price  
dakle zadatak je bio ovako nesto
ako je 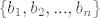 baza za baza za 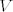 dokazite da je dokazite da je 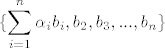 baza za baza za 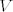 akko je akko je 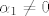
dokazimo da ako je 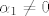 da je onda da je onda 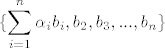 baza za baza za 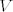
mora se samo dokazat da je 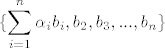 linearno nezavisno linearno nezavisno
pretpostavimo suprotno:
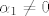 i i 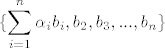 nije linearno nezavisno, sto znaci da postoje skalari nije linearno nezavisno, sto znaci da postoje skalari  koji nisu svi koji nisu svi  i vrijedi i vrijedi 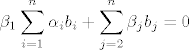
sad to malo "grupiramo" i dobimo:
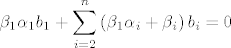
no kako je 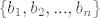 baza slijedi da su svi ovi skalari jednaki baza slijedi da su svi ovi skalari jednaki 
sad se sjetimo pretpostavke bar za jedan 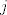 je je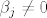
ako je to za 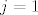 , kako je , kako je 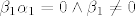 to je to je 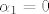 no to je kontradikcija sa pretpostavkom da je no to je kontradikcija sa pretpostavkom da je 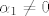
neka je sad 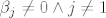 , kako je , kako je
 to je to je 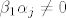 pa je posebno pa je posebno 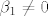 no kako je no kako je 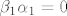 slijedi da je slijedi da je 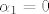 sto je kontradikcija, i time je dokazan ovaj smjer sto je kontradikcija, i time je dokazan ovaj smjer
pokazimo sad da ako je 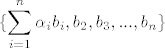 baza da je onda baza da je onda 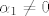
neznam zasto, al opet cu pretpostavit suprotno, neka je ono baza i neka je 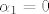
sad, jer je ono baza, onda je i linearno nezavisno pa je 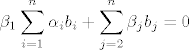 samo kada su svi samo kada su svi 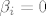 , pogledajmo je li to zaista tako , pogledajmo je li to zaista tako
grupiramo ono malo i uvazimo da je 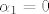
sada dobivamo:
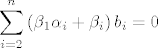
sad, ili su mi svi 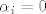 za za 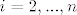 , ili bar jedan nije , ili bar jedan nije
ako su svi  ondauzme ondauzme 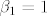 i imam kontradikciju, ako bar jedan nije, npr ako je i imam kontradikciju, ako bar jedan nije, npr ako je 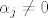 za neki za neki 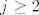 onda stavim da je onda stavim da je 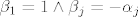 i opet imam kontradikciju i opet imam kontradikciju
time je tvrdnja dokazana
nadam se da je ok rijeseno, i da ce pomoc
... mozda se moze i krace, al... eto... ja sam ovako 
_________________
Mario Berljafa
|




