| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 17:56 sub, 24. 10. 2009 Naslov: Postano: 17:56 sub, 24. 10. 2009 Naslov: |
    |
|
|
pitaj šta te točno zanima
čisto sumnjam da će ti netko stavljat na forum rješenja
pitaj šta te točno zanima
čisto sumnjam da će ti netko stavljat na forum rješenja
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
GoranV
Forumaš(ica)

Pridružen/a: 20. 11. 2008. (11:22:01)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
 Postano: 18:27 sub, 24. 10. 2009 Naslov: Postano: 18:27 sub, 24. 10. 2009 Naslov: |
    |
|
|
to je ovaj sqrt(pi^cos(x))?
ne znam pisat latex, pa bi ovo moglo malo gadno postat
1<= sqrt(pi^cos(x)) <= 2 / ^2 što smijemo jer je kvadriranje neprekidna funkcija pa ne mijenja znak nejednakosti, al naučit ćete vi to već :P
1<=pi^cos(x) <= 4
to daje dva uvjeta
pi^cos(x) >= 1 i pi^cos(x) <= 4
iz prvoga slijedi da cos(x) >= 0 (1 = pi^0)
iz drugog, drugi je zapravo besmislen jer je pi^cos(x) uvijek manje il jednako od pi, pa je u drugome rješenje čitav R
dakle, jedini uvjet je cos(x) >= 0 pa je x element od [3pi/2 + 2kpi, pi/2+2kpi]
to bi trebalo bit to
to je ovaj sqrt(pi^cos(x))?
ne znam pisat latex, pa bi ovo moglo malo gadno postat
1⇐ sqrt(pi^cos(x)) ⇐ 2 / ^2 što smijemo jer je kvadriranje neprekidna funkcija pa ne mijenja znak nejednakosti, al naučit ćete vi to već 
1⇐pi^cos(x) ⇐ 4
to daje dva uvjeta
pi^cos(x) >= 1 i pi^cos(x) ⇐ 4
iz prvoga slijedi da cos(x) >= 0 (1 = pi^0)
iz drugog, drugi je zapravo besmislen jer je pi^cos(x) uvijek manje il jednako od pi, pa je u drugome rješenje čitav R
dakle, jedini uvjet je cos(x) >= 0 pa je x element od [3pi/2 + 2kpi, pi/2+2kpi]
to bi trebalo bit to
_________________ Sedam je prost broj 
Bolonja je smeće i to pod hitno treba mijenjat |
|
| [Vrh] |
|
GoranV
Forumaš(ica)

Pridružen/a: 20. 11. 2008. (11:22:01)
Postovi: (F)16
Spol: 
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 19:28 sub, 24. 10. 2009 Naslov: Postano: 19:28 sub, 24. 10. 2009 Naslov: |
    |
|
|
Bilo bi korisno možda da kažeš što si do sada pokušao, pa da vidimo u čemu je stvar, pogotovo što je 2. zadatak u 2. grupi gotovo isti kao onaj u prvoj grupi, a 4. b) gotovo isti kao onaj u 4. grupi.
Uglavnom, evo neke ideje rješenja:
2. Prikaži [latex]f[/latex] kao kompoziciju funkcija [latex]f_1(x)=\frac{1+x}{1-x}[/latex] (ako želiš, možeš i to rastaviti na kompoziciju jednostavnijih, što ćeš zapravo implicitno ionako raditi pri crtanju grafa: [latex]\frac{1+x}{1-x}=-1+\frac{2}{1-x}[/latex]), [latex]f_2=\cosh (x)+1[/latex] (i to opet možeš podijeliti na kompoziciju funkcija [latex]\cosh x[/latex] i [latex]x+1[/latex], ako ti je prezbunjujuće raditi s funkcijom [latex]\cosh (x)+1[/latex]).
Sad lako odrediš sliku funkcije (i sliku na određenom intervalu) s formulom [latex]f(A)=f_2(f_1(A))[/latex], pri čemu su funkcije [latex]f_1[/latex] i [latex]f_2[/latex] dovoljno jednostavne da slike intervala koji će ti trebati možeš čitati s grafa i/ili računski odrediti.
4. b) Budući da tvrdnja vrijedi za sve podskupove [latex]A[/latex] i [latex]B[/latex] od [latex]\mathbb{R}[/latex], vrijedi i za [latex]A=\{x\}[/latex], [latex]B=\{y\}[/latex], gdje su [latex]x[/latex] i [latex]y[/latex] proizvoljni realni brojevi. Pretpostavimo suprotno: da [latex]f[/latex] nije injekcija. To znači da postoje neki različiti [latex]x[/latex] i [latex]y[/latex] takvi da je [latex]f(x)=f(y)[/latex]. Uvrsti sad u uvjet zadatka [latex]A[/latex] i [latex]B[/latex] definirane na spomenuti način i utvrdi što dobivaš.
Evo, nadam se da sam bio od pomoći, reci ako treba još :).
Addendum: Suza je (bar mislim :D) uglavnom u pravu, to su i po mojoj procjeni rješenja, s tim da bi u 2. zadatku intervali trebali ići [latex][\cosh(-2)+1,\cosh(-3)+1\rangle[/latex], a ne obrnuto, ako se ne varam. Fali rješenje prvog dijela 2. zadatka, ali to mi se čini dosta jednostavno: [latex]R_f=[2,+\infty\rangle[/latex].
Bilo bi korisno možda da kažeš što si do sada pokušao, pa da vidimo u čemu je stvar, pogotovo što je 2. zadatak u 2. grupi gotovo isti kao onaj u prvoj grupi, a 4. b) gotovo isti kao onaj u 4. grupi.
Uglavnom, evo neke ideje rješenja:
2. Prikaži  kao kompoziciju funkcija kao kompoziciju funkcija 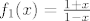 (ako želiš, možeš i to rastaviti na kompoziciju jednostavnijih, što ćeš zapravo implicitno ionako raditi pri crtanju grafa: (ako želiš, možeš i to rastaviti na kompoziciju jednostavnijih, što ćeš zapravo implicitno ionako raditi pri crtanju grafa: 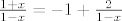 ), ), 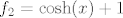 (i to opet možeš podijeliti na kompoziciju funkcija (i to opet možeš podijeliti na kompoziciju funkcija 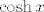 i i 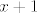 , ako ti je prezbunjujuće raditi s funkcijom , ako ti je prezbunjujuće raditi s funkcijom 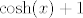 ). ).
Sad lako odrediš sliku funkcije (i sliku na određenom intervalu) s formulom 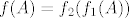 , pri čemu su funkcije , pri čemu su funkcije 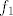 i i 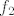 dovoljno jednostavne da slike intervala koji će ti trebati možeš čitati s grafa i/ili računski odrediti. dovoljno jednostavne da slike intervala koji će ti trebati možeš čitati s grafa i/ili računski odrediti.
4. b) Budući da tvrdnja vrijedi za sve podskupove  i i  od od  , vrijedi i za , vrijedi i za 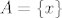 , , 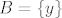 , gdje su , gdje su  i i  proizvoljni realni brojevi. Pretpostavimo suprotno: da proizvoljni realni brojevi. Pretpostavimo suprotno: da  nije injekcija. To znači da postoje neki različiti nije injekcija. To znači da postoje neki različiti  i i  takvi da je takvi da je 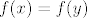 . Uvrsti sad u uvjet zadatka . Uvrsti sad u uvjet zadatka  i i  definirane na spomenuti način i utvrdi što dobivaš. definirane na spomenuti način i utvrdi što dobivaš.
Evo, nadam se da sam bio od pomoći, reci ako treba još  . .
Addendum: Suza je (bar mislim  ) uglavnom u pravu, to su i po mojoj procjeni rješenja, s tim da bi u 2. zadatku intervali trebali ići ) uglavnom u pravu, to su i po mojoj procjeni rješenja, s tim da bi u 2. zadatku intervali trebali ići 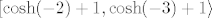 , a ne obrnuto, ako se ne varam. Fali rješenje prvog dijela 2. zadatka, ali to mi se čini dosta jednostavno: , a ne obrnuto, ako se ne varam. Fali rješenje prvog dijela 2. zadatka, ali to mi se čini dosta jednostavno: 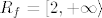 . .
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 8:02 ned, 25. 10. 2009 Naslov: Postano: 8:02 ned, 25. 10. 2009 Naslov: |
    |
|
|
OK, ovaj post će biti dug. Kratkoća mi ne ide :D.
[quote="maty321"]hvala...
znaci mogu samo ostaviti takav kosinus, netrebam uvrštavati riješenja u ono u što se on raspisuje??? demosi su drugacije mi pokazali pa... ovo ce isto biti u redu???[/quote]
Ne bih te sad želio koštati boda-dva (ni proturječiti ostalim demosima... možda oni imaju neke informacije), pa neću reći da će 100% sigurno biti u redu ako rješenje može ostaviš u obliku, na primjer, [latex]\cosh 2[/latex].
Meni je razumno da bi se to moglo zato što nećeš postati ništa pametniji kad umjesto toga napišeš [latex]\frac{e^2+e^{-2}}{2}[/latex]. Moje je razmišljanje da onako barem znaš gdje bi to negdje bilo na grafu kosinusa hiperbolnog, a ovo baš nema neki koristan izgled.
Naravno, možda bi bilo korisno napisati to i u obliku [latex]\frac{e^2+e^{-2}}{2}[/latex] jer se tako, ako ništa, barem pokazuje da znaš definiciju [latex]\cosh[/latex]. Tako da je sigurno najbolje da napišeš oboje, što ti u svakom slučaju neće uzeti puno vremena (rekao bih da ne moraš ništa "uljepšavati" ovaj ružan izraz za [latex]\cosh[/latex], izraz je ružan kako god ga pogledaš). Naravno, možda ti se nešto negdje pokrati zbog svojstva nekih funkcija ili dobiješ neku poznatu vrijednost: na primjer, [latex]\cosh 2 -\cosh -2+\cosh 0[/latex] ipak bi bilo korektno napisati u obliku nešto trivijalnijeg broja [latex]1[/latex] :P.
[quote="maty321"]i da kad rastavim fju na kompoziciju i trebam odrediti sliku, otprilike znam kako ide ali jako puno razmisljam...
aj mi objasni na temelju 2zad!!![/quote]
Dakle, ideja je da funkciju rastavimo na što jednostavnije dijelove koje onda komponiramo. Pogledaj ovako (sad ću ići do krajnje trivijalnih funkcija, ti neke možeš i napamet komponirati i čitati njihovu sliku ako si siguran da nećeš pogriješiti), probat ću sad dati rješenje i neku motivaciju zašto to radimo na primjeru tog zadatka, makar sam to, siguran sam, govorilo i na predavanjima i na vježbama :P.
Vidimo da ćemo se, kao prvo, s ovom jedinicom (van [latex]\cosh[/latex] ) lako nositi, pa je možda korisno razmišljati ovako: [latex]f(x)=f_1(x)+1[/latex], gdje je [latex]f_1(x)=\cosh(\frac{1+x}{1-x})[/latex]. Primijeti da sad zapravo imamo [latex]f(x)=(f_2\circ f_1)(x)[/latex], gdje je [latex]f_2(x)=x+1[/latex].
Idemo sad dalje, budući da nam je [latex]f_1[/latex] još uvijek relativno teška funkcija. S kosinusom hiperbolnim znamo raditi (ako ništa, onda s grafa), pa nas zapravo najviše interesira da probamo nekako shvatiti što se događa u [latex]\frac{1+x}{1-x}[/latex]. To nam daje motivaciju za funkcije [latex]f_3(x)=\cosh x[/latex] i [latex]f_4(x)=\frac{1+x}{1-x}[/latex]. Sad imamo [latex]f_1(x)=(f_3\circ f_4)(x)[/latex], tj. [latex]f(x)=(f_2\circ f_3\circ f_4)(x)[/latex]. Dobro. Ostaje nam dakle [latex]f_4[/latex]. Možda s njom možemo i direktnije raditi, ali ja ću ipak sada ići do krajnje jednostavnih funkcija, naravno da ti ne moraš ako se osjećaš dovoljno siguran.
Dakle, [latex]f_4[/latex] bismo ipak željeli još malo bolje pogledati. Vrijedi [latex]\frac{1+x}{1-x}=\frac{-(1-x)+2}{1-x}=-1+\frac{2}{1-x}=-1-\frac{2}{x-1}[/latex] (ovo namještanje brojnika je inače stari "trik" na koji funkciju svodimo na jednostavniji oblik budući da nam je teško zamisliti funkciju koja ima linearni polinom u brojniku i linearni polinom u nazivniku).
OK. Sad smo već pri kraju. Znamo da s ovim [latex]-1[/latex] na početku nećemo imati problema, pa uzimamo [latex]f_4(x)=-1+f_5(x)[/latex], gdje je [latex]f_5(x)=\frac{-2}{x-1}[/latex]. Vrijedi, naravno, [latex]f_4(x)=(f_6\circ f_5)(x)[/latex], gdje je [latex]f_6(x)=x-1[/latex]. Stoga imamo [latex]f(x)=(f_2\circ f_3\circ f_6\circ f_5)(x)[/latex]. Još ćemo malo pojednostaviti [latex]f_5[/latex]. Vidimo da nam ona iznosi [latex]-2f_7[/latex], gdje je [latex]f_7(x)=\frac{1}{x-1}[/latex], pa je [latex]f_5=f_8\circ f_7[/latex], gdje je [latex]f_8(x)=-2x[/latex] Dakle, [latex]f(x)=(f_2\circ f_3\circ f_6\circ f_8\circ f_7)(x)[/latex]. Makar je ovo već jako jednostavno, želimo stvari pojednostaviti do krajnjih granica, pa ćemo prikazati [latex]f_7[/latex] u obliku [latex]\frac{1}{f_9}[/latex], gdje je [latex]f_9(x)=x-1[/latex]. Dakle, [latex]f_7=f_{10}\circ f_9[/latex], gdje je [latex]f_{10}(x)=\frac{1}{x}[/latex].
Stoga imamo [latex]f(x)=(f_2\circ f_3\circ f_6\circ f_8\circ f_{10}\circ f_9)(x)[/latex]. Sve funkcije u kompoziciji izuzetno su jednostavne (kažem, ako si dovoljno siguran, možeš taj proces rastavljanja na kompozicije prekinuti u trenutku kad dobiješ funkcije koje su ti dovoljno jednostavne za rad), pa nemamo problema s određivanjem njihove slike na bilo kojem dijelu domene. Sad koristimo formulu [latex]f(A)=(f_2\circ f_3\circ f_6\circ f_8\circ f_{10}\circ f_9)(A)[/latex]. Za [latex]A[/latex] u prvom dijelu zadatka uzimamo [latex]\mathbb{R}\setminus\{1\}[/latex], a u drugom [latex]\langle 2, 3][/latex]. Lako dobivamo rješenja iz toga.
Nadam se da sam uspio objasniti tok razmišljanja koji stoji iza ovoga, a praksa (iliti "kako se toga sjetiti baš u ovom zadatku") dolazi, kao i sve druge lijepe stvari, vježbom (ili posjedovanjem ogromnih količina poznanstava i šarenih papira, ali dvojim da bi ti to pomoglo u rješavanju ovog zadatka :D) i vidjet ćeš, kad shvatiš kako to ide i probaš na par zadataka, prirodno se toga sjetiš :).
OK, ovaj post će biti dug. Kratkoća mi ne ide  . .
| maty321 (napisa): | hvala...
znaci mogu samo ostaviti takav kosinus, netrebam uvrštavati riješenja u ono u što se on raspisuje??? demosi su drugacije mi pokazali pa... ovo ce isto biti u redu??? |
Ne bih te sad želio koštati boda-dva (ni proturječiti ostalim demosima... možda oni imaju neke informacije), pa neću reći da će 100% sigurno biti u redu ako rješenje može ostaviš u obliku, na primjer, 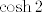 . .
Meni je razumno da bi se to moglo zato što nećeš postati ništa pametniji kad umjesto toga napišeš 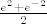 . Moje je razmišljanje da onako barem znaš gdje bi to negdje bilo na grafu kosinusa hiperbolnog, a ovo baš nema neki koristan izgled. . Moje je razmišljanje da onako barem znaš gdje bi to negdje bilo na grafu kosinusa hiperbolnog, a ovo baš nema neki koristan izgled.
Naravno, možda bi bilo korisno napisati to i u obliku 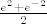 jer se tako, ako ništa, barem pokazuje da znaš definiciju jer se tako, ako ništa, barem pokazuje da znaš definiciju 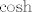 . Tako da je sigurno najbolje da napišeš oboje, što ti u svakom slučaju neće uzeti puno vremena (rekao bih da ne moraš ništa "uljepšavati" ovaj ružan izraz za . Tako da je sigurno najbolje da napišeš oboje, što ti u svakom slučaju neće uzeti puno vremena (rekao bih da ne moraš ništa "uljepšavati" ovaj ružan izraz za 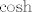 , izraz je ružan kako god ga pogledaš). Naravno, možda ti se nešto negdje pokrati zbog svojstva nekih funkcija ili dobiješ neku poznatu vrijednost: na primjer, , izraz je ružan kako god ga pogledaš). Naravno, možda ti se nešto negdje pokrati zbog svojstva nekih funkcija ili dobiješ neku poznatu vrijednost: na primjer, 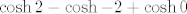 ipak bi bilo korektno napisati u obliku nešto trivijalnijeg broja ipak bi bilo korektno napisati u obliku nešto trivijalnijeg broja   . .
| maty321 (napisa): | i da kad rastavim fju na kompoziciju i trebam odrediti sliku, otprilike znam kako ide ali jako puno razmisljam...
aj mi objasni na temelju 2zad!!! |
Dakle, ideja je da funkciju rastavimo na što jednostavnije dijelove koje onda komponiramo. Pogledaj ovako (sad ću ići do krajnje trivijalnih funkcija, ti neke možeš i napamet komponirati i čitati njihovu sliku ako si siguran da nećeš pogriješiti), probat ću sad dati rješenje i neku motivaciju zašto to radimo na primjeru tog zadatka, makar sam to, siguran sam, govorilo i na predavanjima i na vježbama  . .
Vidimo da ćemo se, kao prvo, s ovom jedinicom (van 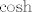 ) lako nositi, pa je možda korisno razmišljati ovako: ) lako nositi, pa je možda korisno razmišljati ovako: 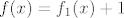 , gdje je , gdje je 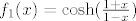 . Primijeti da sad zapravo imamo . Primijeti da sad zapravo imamo 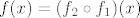 , gdje je , gdje je 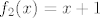 . .
Idemo sad dalje, budući da nam je 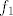 još uvijek relativno teška funkcija. S kosinusom hiperbolnim znamo raditi (ako ništa, onda s grafa), pa nas zapravo najviše interesira da probamo nekako shvatiti što se događa u još uvijek relativno teška funkcija. S kosinusom hiperbolnim znamo raditi (ako ništa, onda s grafa), pa nas zapravo najviše interesira da probamo nekako shvatiti što se događa u 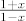 . To nam daje motivaciju za funkcije . To nam daje motivaciju za funkcije 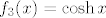 i i 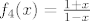 . Sad imamo . Sad imamo 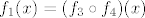 , tj. , tj. 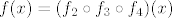 . Dobro. Ostaje nam dakle . Dobro. Ostaje nam dakle 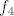 . Možda s njom možemo i direktnije raditi, ali ja ću ipak sada ići do krajnje jednostavnih funkcija, naravno da ti ne moraš ako se osjećaš dovoljno siguran. . Možda s njom možemo i direktnije raditi, ali ja ću ipak sada ići do krajnje jednostavnih funkcija, naravno da ti ne moraš ako se osjećaš dovoljno siguran.
Dakle, 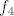 bismo ipak željeli još malo bolje pogledati. Vrijedi bismo ipak željeli još malo bolje pogledati. Vrijedi 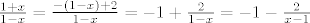 (ovo namještanje brojnika je inače stari "trik" na koji funkciju svodimo na jednostavniji oblik budući da nam je teško zamisliti funkciju koja ima linearni polinom u brojniku i linearni polinom u nazivniku). (ovo namještanje brojnika je inače stari "trik" na koji funkciju svodimo na jednostavniji oblik budući da nam je teško zamisliti funkciju koja ima linearni polinom u brojniku i linearni polinom u nazivniku).
OK. Sad smo već pri kraju. Znamo da s ovim  na početku nećemo imati problema, pa uzimamo na početku nećemo imati problema, pa uzimamo 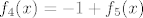 , gdje je , gdje je 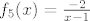 . Vrijedi, naravno, . Vrijedi, naravno, 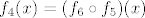 , gdje je , gdje je 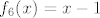 . Stoga imamo . Stoga imamo 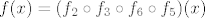 . Još ćemo malo pojednostaviti . Još ćemo malo pojednostaviti 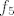 . Vidimo da nam ona iznosi . Vidimo da nam ona iznosi 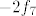 , gdje je , gdje je 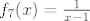 , pa je , pa je 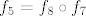 , gdje je , gdje je 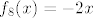 Dakle, Dakle,  . Makar je ovo već jako jednostavno, želimo stvari pojednostaviti do krajnjih granica, pa ćemo prikazati . Makar je ovo već jako jednostavno, želimo stvari pojednostaviti do krajnjih granica, pa ćemo prikazati 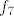 u obliku u obliku 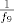 , gdje je , gdje je 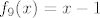 . Dakle, . Dakle, 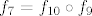 , gdje je , gdje je 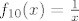 . .
Stoga imamo 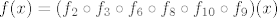 . Sve funkcije u kompoziciji izuzetno su jednostavne (kažem, ako si dovoljno siguran, možeš taj proces rastavljanja na kompozicije prekinuti u trenutku kad dobiješ funkcije koje su ti dovoljno jednostavne za rad), pa nemamo problema s određivanjem njihove slike na bilo kojem dijelu domene. Sad koristimo formulu . Sve funkcije u kompoziciji izuzetno su jednostavne (kažem, ako si dovoljno siguran, možeš taj proces rastavljanja na kompozicije prekinuti u trenutku kad dobiješ funkcije koje su ti dovoljno jednostavne za rad), pa nemamo problema s određivanjem njihove slike na bilo kojem dijelu domene. Sad koristimo formulu 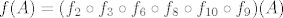 . Za . Za  u prvom dijelu zadatka uzimamo u prvom dijelu zadatka uzimamo 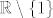 , a u drugom , a u drugom 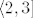 . Lako dobivamo rješenja iz toga. . Lako dobivamo rješenja iz toga.
Nadam se da sam uspio objasniti tok razmišljanja koji stoji iza ovoga, a praksa (iliti "kako se toga sjetiti baš u ovom zadatku") dolazi, kao i sve druge lijepe stvari, vježbom (ili posjedovanjem ogromnih količina poznanstava i šarenih papira, ali dvojim da bi ti to pomoglo u rješavanju ovog zadatka  ) i vidjet ćeš, kad shvatiš kako to ide i probaš na par zadataka, prirodno se toga sjetiš ) i vidjet ćeš, kad shvatiš kako to ide i probaš na par zadataka, prirodno se toga sjetiš  . .
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
Milojko
Forumaš(ica)


Pridružen/a: 07. 11. 2008. (14:57:52)
Postovi: (453)16
Spol: 
Lokacija: Hilbertov hotel
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
mornik
Forumaš(ica)

Pridružen/a: 26. 09. 2009. (06:25:44)
Postovi: (128)16
|
 Postano: 15:49 ned, 25. 10. 2009 Naslov: Postano: 15:49 ned, 25. 10. 2009 Naslov: |
    |
|
|
Nisam baš siguran da sam dobro shvatio pitanje... uglavnom, trebaš odrediti [latex]\{f(x): x\in A\}[/latex], gdje je [latex]A[/latex] skup (specijalno, u tvom slučaju je [latex]A[/latex] interval). (Mislim da na vježbama to radite "s grafa", ako su funkcije dovoljno jednostavne kao, npr. [latex]x^2[/latex] ili [latex]\frac{1}{x}[/latex]. Inače ih kompozicijom svedete opet na jednostavnije funkcije.)
Nema veze preslikaju li se rubovi intervala u istu točku - mi tražimo sliku funkcije na cijelom intervalu, a to ne radimo tako da samo odredimo vrijednosti funkcije na rubovima intervala i onda ih povežemo. Na primjer, pogledajmo sliku funkcije [latex]f(x)=x^2[/latex] na intervalu [latex][-2,2][/latex]. I [latex]-2[/latex] i [latex]2[/latex] se preslikaju u [latex]4[/latex], ali svejedno je [latex]f([-2,2])=[0,4].[/latex] Uzgred, očito vrijedi i [latex]f(\langle -2,2])=[0,4][/latex], tako da vidimo da "otvorenost" intervala kojeg dobivamo općenito nema nikakve veze s "otvorenošću" polaznog intervala.
Naravno, ako je, specijalno, na tom cijelom intervalu funkcija konstantna, onda je slika od funkcije na tom intervalu naprosto [latex]\{c\}[/latex], gdje je [latex]c[/latex] ta konstanta. Ali to je samo jedan specijalan slučaj.
Ukratko, ne zanimaju te samo rubne točke, već te, da odrediš sliku, zanima i kako se funkcija ponaša između njih, a ako je dovoljno jednostavna, s tim nećeš imati problema (pogotovo ako čitaš s grafa, što jest malo neprecizno, ali se u nedostatku jačih alata tako radi, pogotovo na početku semestra).
Nadam se da nisam potpuno pogriješio sadržaj tvojeg pitanja :D.
Nisam baš siguran da sam dobro shvatio pitanje... uglavnom, trebaš odrediti 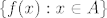 , gdje je , gdje je  skup (specijalno, u tvom slučaju je skup (specijalno, u tvom slučaju je  interval). (Mislim da na vježbama to radite "s grafa", ako su funkcije dovoljno jednostavne kao, npr. interval). (Mislim da na vježbama to radite "s grafa", ako su funkcije dovoljno jednostavne kao, npr. 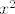 ili ili  . Inače ih kompozicijom svedete opet na jednostavnije funkcije.) . Inače ih kompozicijom svedete opet na jednostavnije funkcije.)
Nema veze preslikaju li se rubovi intervala u istu točku - mi tražimo sliku funkcije na cijelom intervalu, a to ne radimo tako da samo odredimo vrijednosti funkcije na rubovima intervala i onda ih povežemo. Na primjer, pogledajmo sliku funkcije 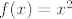 na intervalu na intervalu 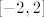 . I . I 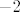 i i  se preslikaju u se preslikaju u 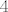 , ali svejedno je , ali svejedno je 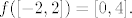 Uzgred, očito vrijedi i Uzgred, očito vrijedi i 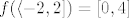 , tako da vidimo da "otvorenost" intervala kojeg dobivamo općenito nema nikakve veze s "otvorenošću" polaznog intervala. , tako da vidimo da "otvorenost" intervala kojeg dobivamo općenito nema nikakve veze s "otvorenošću" polaznog intervala.
Naravno, ako je, specijalno, na tom cijelom intervalu funkcija konstantna, onda je slika od funkcije na tom intervalu naprosto 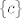 , gdje je , gdje je  ta konstanta. Ali to je samo jedan specijalan slučaj. ta konstanta. Ali to je samo jedan specijalan slučaj.
Ukratko, ne zanimaju te samo rubne točke, već te, da odrediš sliku, zanima i kako se funkcija ponaša između njih, a ako je dovoljno jednostavna, s tim nećeš imati problema (pogotovo ako čitaš s grafa, što jest malo neprecizno, ali se u nedostatku jačih alata tako radi, pogotovo na početku semestra).
Nadam se da nisam potpuno pogriješio sadržaj tvojeg pitanja  . .
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 14:30 uto, 27. 10. 2009 Naslov: Postano: 14:30 uto, 27. 10. 2009 Naslov: |
    |
|
|
Ako dobro iscitavam funkciju, onda je
[latex]f(x) = (\mathrm{ctg}\ x - 1)^2 + 1[/latex].
Sada uzmes da je y proizvoljan i probas dobiti x. Brzo se vidi da za y = 0 treba biti [latex](\mathrm{ctg}\ x - 1)^2 = -1[/latex], sto znaci da nula nema prasliku, pa funkcija nije surjekcija.
Ako dobro iscitavam funkciju, onda je
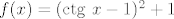 . .
Sada uzmes da je y proizvoljan i probas dobiti x. Brzo se vidi da za y = 0 treba biti 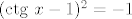 , sto znaci da nula nema prasliku, pa funkcija nije surjekcija. , sto znaci da nula nema prasliku, pa funkcija nije surjekcija.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
|












