Baza za V^3(O) (zadatak)

[Jay-Mo]

Provjerite cine li vektori ,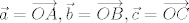
gdje je
1. A = (1, 2, 1), B = (1, 1, 0), C = (0, 1, 1)
2. A = (1, 0, -1), B = (1, 2, 3), C = (0, 1, 1)
bazu za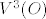



Ja vidim da da primjer pod 1 ne cini bazu jer se svaki moze prikazati kao kombinaciju ostalih, ali kako ovaj pod dva, moze li mi netko napisati kako to lijepo treba dokazati od A do Ž!


HVALA!!

[there is no spoon]

za drugi probas dokazati da cine bazu, tj povjeri da li za povlaci

[Luuka]

Najjednostavnije :
Staviš ih u matricu i izračunaš determinantu. Ako je det=0, onda su linearno zavisni, ako nije 0 onda su lin nezavisni, ima ih 3 u prostoru dimenzije 3, pa su baza.

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[.anchy.]

@Luuka: nisu još radili matrice,a kamoli determinante..
znači imaš:
a(1,0,-1)+b(1,2,3)+c(0,1,1)=(0,0,0)

(a+b,2b+c,-a+3b+c)=(0,0,0)

ovo je laički: to dobiš tako da na prvo mjesto vektora staviš zbroj prvih mjesta ovih gore vektora pomnoženih s a,b ili c:
1*a+1*b+0*c
tak i za drugo mjesto:
0*a+2*b+1*c
isto tako za treće mjesto
i sad imaš sustav
a+b=0
2b+c=0
-a+3b+c=0

i oni čine bazu ako je rješenje sustava samo trivijalno,tj.da su a,b i c 0.

[Jay-Mo]

Hvala svima, skuzio sam!!

[Luuka]