| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
angi
Gost
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
 Postano: 17:23 pon, 2. 11. 2009 Naslov: Postano: 17:23 pon, 2. 11. 2009 Naslov: |
    |
|
|
ja sam dobio da je prirodna domena R^2\{(2k,0)|k element Z}
gomilište je cijeli R^2
a pod c) jasno je da je fj-a neprekidna na domeni(to se objasni lijepo), pa tamo ima i limes, i u točki (0,0) ima limes, u ostalim gomilištima nema...
tako je meni ispalo, jel mi dobro to??
ja sam dobio da je prirodna domena R^2\{(2k,0)|k element Z}
gomilište je cijeli R^2
a pod c) jasno je da je fj-a neprekidna na domeni(to se objasni lijepo), pa tamo ima i limes, i u točki (0,0) ima limes, u ostalim gomilištima nema...
tako je meni ispalo, jel mi dobro to??
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
 Postano: 17:24 pon, 2. 11. 2009 Naslov: Postano: 17:24 pon, 2. 11. 2009 Naslov: |
    |
|
|
[b]a)[/b]
Prirodna domena je [latex]\mathbb{R} \backslash (2k, 0), k \in \mathbb{Z}[/latex]
[b]b)[/b]
Skup svih gomilišta je cijeli [latex]\mathbb{R}[/latex]
Nadam se da oko podzadataka [b]a)[/b] i [b]b)[/b] nema problema.
[b]c)[/b]
Pogledaj restrikciju [latex]f(2k, y)[/latex] kad [latex]y \to 0 [/latex], dakle:
[latex]f(2k, y) = \frac{2ky(2k + y - 4)}{0 + y^2}[/latex]
odavde vids da kad [latex]y \to 0 [/latex] funkcija divergira [latex]\forall k \neq 0, 2[/latex]
kada je [latex]k = 0[/latex] limes ove restrikcije je [latex]0[/latex], kada je [latex]k = 2[/latex] limes je 4.
Sad je još potrebno naći neki niz koji teži u [latex](0, 0)[/latex] a da mu je limes razlicit od [latex]0[/latex], te analogno za [latex](4, 0)[/latex].
Za [latex](4, 0)[/latex] dovoljno je uzeti niz [latex]\left( 4-\frac{1}{n}, \frac{1}{n} \right)[/latex], dok za [latex](0, 0)[/latex] uzmeš niz [latex]\left( \frac{1}{n}, \frac{\pi^2}{4n} \right)[/latex]. Sada ti član u brojniku ([latex]xy[/latex]) postaje [latex]\frac{\pi^2}{4n^2}[/latex], podijeliš i brojnik i nazivnik sa njime i iskoristiš činjenicu:
[latex]\lim_{x \to 0}{\frac{sin x}{x}} = 1[/latex] i dobiješ limes razlicit od 0.
Nadam se da je pomoglo.
Pozdrav, Marko
a)
Prirodna domena je 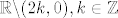
b)
Skup svih gomilišta je cijeli 
Nadam se da oko podzadataka a) i b) nema problema.
c)
Pogledaj restrikciju 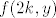 kad kad 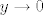 , dakle: , dakle:
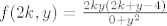
odavde vids da kad 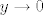 funkcija divergira funkcija divergira 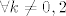
kada je 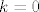 limes ove restrikcije je limes ove restrikcije je  , kada je , kada je 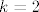 limes je 4. limes je 4.
Sad je još potrebno naći neki niz koji teži u 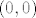 a da mu je limes razlicit od a da mu je limes razlicit od  , te analogno za , te analogno za 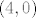 . .
Za 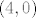 dovoljno je uzeti niz dovoljno je uzeti niz 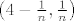 , dok za , dok za 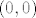 uzmeš niz uzmeš niz 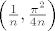 . Sada ti član u brojniku ( . Sada ti član u brojniku (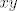 ) postaje ) postaje 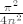 , podijeliš i brojnik i nazivnik sa njime i iskoristiš činjenicu: , podijeliš i brojnik i nazivnik sa njime i iskoristiš činjenicu:
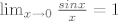 i dobiješ limes razlicit od 0. i dobiješ limes razlicit od 0.
Nadam se da je pomoglo.
Pozdrav, Marko
_________________
reductio ad absurdum
|
|
| [Vrh] |
|
ToMeK
Forumaš(ica)

Pridružen/a: 12. 09. 2008. (17:22:06)
Postovi: (BA)16
Spol: 
|
|
| [Vrh] |
|
angi
Gost
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
angi
Gost
|
 Postano: 18:28 pon, 2. 11. 2009 Naslov: Postano: 18:28 pon, 2. 11. 2009 Naslov: |
    |
|
|
Sad je još potrebno naći neki niz koji teži u (0,0)a da mu je limes razlicit od 0, te analogno za (4,0).
Za (4,0) dovoljno je uzeti niz (4-1/n,1/n)?
to neznam raspisati??????
Sad je još potrebno naći neki niz koji teži u (0,0)a da mu je limes razlicit od 0, te analogno za (4,0).
Za (4,0) dovoljno je uzeti niz (4-1/n,1/n)?
to neznam raspisati??????
|
|
| [Vrh] |
|
mycky1111
Forumaš(ica)

Pridružen/a: 26. 05. 2008. (11:59:07)
Postovi: (D4)16
Spol: 
|
|
| [Vrh] |
|
angi
Gost
|
 Postano: 18:39 pon, 2. 11. 2009 Naslov: Postano: 18:39 pon, 2. 11. 2009 Naslov: |
    |
|
|
a jesam,i dobijen da je lmes=0,(a gore pise "Sad je još potrebno naći neki niz koji teži u (0,0)a da mu je limes razlicit od 0, te analogno za(4,0) ),znaci da mi nes ne vlja a nemogu naci gresku
a jesam,i dobijen da je lmes=0,(a gore pise "Sad je još potrebno naći neki niz koji teži u (0,0)a da mu je limes razlicit od 0, te analogno za(4,0) ),znaci da mi nes ne vlja a nemogu naci gresku
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
angi
Gost
|
|
| [Vrh] |
|
suncica
Gost
|
 Postano: 18:48 pon, 2. 11. 2009 Naslov: Postano: 18:48 pon, 2. 11. 2009 Naslov: |
    |
|
|
ej ljudi pozz svima,aj ako bi neko bio dobar i pomogao mi rjesiti 6.zad iz kol 2007.god,mi na vjezbama smo rjesili samo jedan takav zad.,a meni nije bas prejasno,pa ak neko moze raspisati i rjesiti,puno puno hvala
:lol:
ej ljudi pozz svima,aj ako bi neko bio dobar i pomogao mi rjesiti 6.zad iz kol 2007.god,mi na vjezbama smo rjesili samo jedan takav zad.,a meni nije bas prejasno,pa ak neko moze raspisati i rjesiti,puno puno hvala

|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
angi
Gost
|
|
| [Vrh] |
|
markotron
Forumaš(ica)

Pridružen/a: 26. 10. 2008. (12:07:29)
Postovi: (95)16
Spol: 
Lokacija: Umag
|
|
| [Vrh] |
|
ddduuu
Forumaš(ica)

Pridružen/a: 16. 11. 2008. (12:31:48)
Postovi: (109)16
|
|
| [Vrh] |
|
|












