| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
majmun
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (12:10:03)
Postovi: (5)16
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
 Postano: 13:03 uto, 3. 11. 2009 Naslov: Postano: 13:03 uto, 3. 11. 2009 Naslov: |
    |
|
|
ja mislim da pisemo i to..al, nisam sigurna..
a, jel pisemo onaj dio gradiva kad imamo npr 3^2009 il tako nesto, jer tog ima u proslim kolokvijima..?
i, jel smijemo imati kalkulator na kolokviju, jer mozda ce nam trebat za indukciju..?
ja mislim da pisemo i to..al, nisam sigurna..
a, jel pisemo onaj dio gradiva kad imamo npr 3^2009 il tako nesto, jer tog ima u proslim kolokvijima..?
i, jel smijemo imati kalkulator na kolokviju, jer mozda ce nam trebat za indukciju..?
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ante c
Forumaš(ica)


Pridružen/a: 10. 10. 2009. (19:18:15)
Postovi: (62)16
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 18:51 uto, 3. 11. 2009 Naslov: Postano: 18:51 uto, 3. 11. 2009 Naslov: |
    |
|
|
opet mislim da nisi dobro napisala :D
reko bi da je zadatak ovo:
[latex]A \cup (B \cap C)=(A \cup B) \cap (A \cup C)[/latex]
pa idemo :D
Neka je [latex] x \in A \cup (B \cap C)[/latex]
to znače 2 slučaja:
1. [latex] x \in A [/latex] ili
2. [latex] x \in B \cap C[/latex]
pa idemo po oba slučaja:
1. znamo da je x iz A, pa je onda i x iz AUB i AUC, pošto su to veći skupovi, pa je i u njihovom presjeku - OK
2. [latex]x \in B \cap C \Rightarrow x \in B \& x \in C [/latex]
to znači da je x iz AUB i AUC, koji su veći skupovi od B i C, pa je i u njihovom presjeku. - OK
u oba slučaja dobili smo što smo trebali, da je x iz desne strane.
Dalje probaj sama, nije teško :D
I btw nemojte ovakve zadatke smatrat pod dokaze, to su sasvim obični zadaci. To što je u textu zadatka "dokaži" ne znači da je to baš neki dokaz. To bi vam vrlo lako moglo doć u kolokviju
opet mislim da nisi dobro napisala 
reko bi da je zadatak ovo:
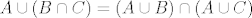
pa idemo 
Neka je 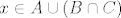
to znače 2 slučaja:
1. 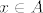 ili ili
2. 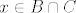
pa idemo po oba slučaja:
1. znamo da je x iz A, pa je onda i x iz AUB i AUC, pošto su to veći skupovi, pa je i u njihovom presjeku - OK
2. 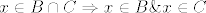
to znači da je x iz AUB i AUC, koji su veći skupovi od B i C, pa je i u njihovom presjeku. - OK
u oba slučaja dobili smo što smo trebali, da je x iz desne strane.
Dalje probaj sama, nije teško 
I btw nemojte ovakve zadatke smatrat pod dokaze, to su sasvim obični zadaci. To što je u textu zadatka "dokaži" ne znači da je to baš neki dokaz. To bi vam vrlo lako moglo doć u kolokviju
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
 Postano: 21:49 uto, 3. 11. 2009 Naslov: Postano: 21:49 uto, 3. 11. 2009 Naslov: |
    |
|
|
[quote="ajaxcy"]Može netko pomoć: kako cu provjerit da je definicija dobra....tj da ne ovisi o izboru predstavnika?!?!
za skup Z i za Q ???
na predavanju smo radili dokaz za Z ali ga ne kuzim; pa shodno tome ne mogu provjerit za Q[/quote]
Pretpostavljam da mislis na zbrajanje i mnozenje na skupu Z sto smo radili na predavanju, pa smo htjeli dokazati da ne ovisi o izboru reprezentanta(predstavnika), tj. da ne vrijedi samo za neke odabrane a i b iz Z, nego i za sve elemente koji su u relaciji s njima, znaci [(a,b)]=[(a1,b1)], pa analogno za neke c i d, [(c,d)]=[(c1,d1)]. Iz prve jednakosti dobijemo a+b1=b+a1, tj. c+d1=d+c1. Definirali smo zbroj u skupu Z kao [(a+c,b+d)] te trebamo dokazati da je to jednako [(a1+c1,b1+d1)]. Kad raspisemo prvi dio jednakosti, imamo (a+c)+(b1+d1)=(a+b1)+(c+d1)=b+a1+d+c1=(b+d)+(a1+c1). Dakle, dokazali smo jednakost, odnosno da zbrajanje ne ovisi o izboru reprezentanta.
Za mnozenje dokazujes da je [(a1,b1)]*[(c1,d1)]=[(a1c1+b1d1,b1c1+a1d1)].
Raspises umnozak, (a1-b1)*(c1-d1)=a1c1-a1d1-b1c1+b1d1=(a1c1+b1d1)-(b1c1+a1d1). Sto je upravo drugi dio jednakosti.
S obzirom da nismo puno spominjali zbrajanje i mnozenje na skupu Q, mislim da se analogno raspisu i po pravilima zbrajanja i mnozenja razlomaka se dokazu. (nap. jedina razlika je postavka relacije na Q, tamo [(a,b)] oznacava a/b.)
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="pajopatak"]Znači ne treba učit sve one dokaze za djeljivost i kongurenciju?
A dali treba učit dokaze za proste brojeve?[/quote]
Pazanin je rekao da djeljivost i kongruencije nece ulazit u ovaj kolokvij, a s njima su bili i prosti brojeve, sto znaci da ne bi trebali bit. Iako, moze stavit djeljivost kao dio nekih relacija (tipa relacija svih a-b koji su djeljivi s 3), ali onih dokaza i kongruencije po onom sto je rekao nece bit.
| ajaxcy (napisa): | Može netko pomoć: kako cu provjerit da je definicija dobra....tj da ne ovisi o izboru predstavnika?!?!
za skup Z i za Q ???
na predavanju smo radili dokaz za Z ali ga ne kuzim; pa shodno tome ne mogu provjerit za Q |
Pretpostavljam da mislis na zbrajanje i mnozenje na skupu Z sto smo radili na predavanju, pa smo htjeli dokazati da ne ovisi o izboru reprezentanta(predstavnika), tj. da ne vrijedi samo za neke odabrane a i b iz Z, nego i za sve elemente koji su u relaciji s njima, znaci [(a,b)]=[(a1,b1)], pa analogno za neke c i d, [(c,d)]=[(c1,d1)]. Iz prve jednakosti dobijemo a+b1=b+a1, tj. c+d1=d+c1. Definirali smo zbroj u skupu Z kao [(a+c,b+d)] te trebamo dokazati da je to jednako [(a1+c1,b1+d1)]. Kad raspisemo prvi dio jednakosti, imamo (a+c)+(b1+d1)=(a+b1)+(c+d1)=b+a1+d+c1=(b+d)+(a1+c1). Dakle, dokazali smo jednakost, odnosno da zbrajanje ne ovisi o izboru reprezentanta.
Za mnozenje dokazujes da je [(a1,b1)]*[(c1,d1)]=[(a1c1+b1d1,b1c1+a1d1)].
Raspises umnozak, (a1-b1)*(c1-d1)=a1c1-a1d1-b1c1+b1d1=(a1c1+b1d1)-(b1c1+a1d1). Sto je upravo drugi dio jednakosti.
S obzirom da nismo puno spominjali zbrajanje i mnozenje na skupu Q, mislim da se analogno raspisu i po pravilima zbrajanja i mnozenja razlomaka se dokazu. (nap. jedina razlika je postavka relacije na Q, tamo [(a,b)] oznacava a/b.)
Added after 3 minutes:
| pajopatak (napisa): | Znači ne treba učit sve one dokaze za djeljivost i kongurenciju?
A dali treba učit dokaze za proste brojeve? |
Pazanin je rekao da djeljivost i kongruencije nece ulazit u ovaj kolokvij, a s njima su bili i prosti brojeve, sto znaci da ne bi trebali bit. Iako, moze stavit djeljivost kao dio nekih relacija (tipa relacija svih a-b koji su djeljivi s 3), ali onih dokaza i kongruencije po onom sto je rekao nece bit.
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
 Postano: 16:48 sri, 4. 11. 2009 Naslov: Postano: 16:48 sri, 4. 11. 2009 Naslov: |
    |
|
|
Ovako, mene zbunjuje jedna stvar.
Recimo da imamo relaciju na skupu S={1,2,3}
[latex] \rho=\{(1,2), (1,3)\}[/latex]
Znam da ova relacija nije refleksivna niti simetrična, ali kako znam da li je antisimetrična ili tranzitivna kad elemente nemam s čime usporediti?
Znači li to automatski da je antisimetrična i tranzitivna ili ne?
Ovako, mene zbunjuje jedna stvar.
Recimo da imamo relaciju na skupu S={1,2,3}
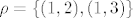
Znam da ova relacija nije refleksivna niti simetrična, ali kako znam da li je antisimetrična ili tranzitivna kad elemente nemam s čime usporediti?
Znači li to automatski da je antisimetrična i tranzitivna ili ne?
|
|
| [Vrh] |
|
|













