| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
|
| [Vrh] |
|
genchy
Forumaš(ica)

Pridružen/a: 03. 09. 2009. (18:32:56)
Postovi: (29)16
|
 Postano: 17:23 sri, 4. 11. 2009 Naslov: Postano: 17:23 sri, 4. 11. 2009 Naslov: |
    |
|
|
[quote="Genaro"]Ovako, mene zbunjuje jedna stvar.
Recimo da imamo relaciju na skupu S={1,2,3}
[latex] \rho=\{(1,2), (1,3)\}[/latex]
Znam da ova relacija nije refleksivna niti simetrična, ali kako znam da li je antisimetrična ili tranzitivna kad elemente nemam s čime usporediti?
Znači li to automatski da je antisimetrična i tranzitivna ili ne?[/quote]
Upravo tako.
Znaci nije refleksivna ni simetricna, dok je antisimetricna i tranzitivna jer, kako bi rekao profesor, "nema di propast". Odnosno, formalnije, implikacije su trivijalno zadovoljene, jer je prvi dio lazan.
| Genaro (napisa): | Ovako, mene zbunjuje jedna stvar.
Recimo da imamo relaciju na skupu S={1,2,3}
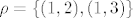
Znam da ova relacija nije refleksivna niti simetrična, ali kako znam da li je antisimetrična ili tranzitivna kad elemente nemam s čime usporediti?
Znači li to automatski da je antisimetrična i tranzitivna ili ne? |
Upravo tako.
Znaci nije refleksivna ni simetricna, dok je antisimetricna i tranzitivna jer, kako bi rekao profesor, "nema di propast". Odnosno, formalnije, implikacije su trivijalno zadovoljene, jer je prvi dio lazan.
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
 Postano: 10:24 čet, 5. 11. 2009 Naslov: Postano: 10:24 čet, 5. 11. 2009 Naslov: |
    |
|
|
Imam i ja jedno pitanje. Ovo je zadatak iz 2.zadaće,13.zadatak.
Na skupu S=[0,2],relacija p je zadana formulom:
xpy akko (x,y e [0,1] ili x,y e <1,2])
Dokažite da je p relacija ekvivalencije i odredite joj klase ekvival.
Ne kužim kako ovo može bit klasa ekvivalencije, jer recimo 0 i 2 nisu u relaciji,nekužim kako se to rješava kada imam intervala,pa ako mi netko može pojasnit malo.
Hvala
Imam i ja jedno pitanje. Ovo je zadatak iz 2.zadaće,13.zadatak.
Na skupu S=[0,2],relacija p je zadana formulom:
xpy akko (x,y e [0,1] ili x,y e <1,2])
Dokažite da je p relacija ekvivalencije i odredite joj klase ekvival.
Ne kužim kako ovo može bit klasa ekvivalencije, jer recimo 0 i 2 nisu u relaciji,nekužim kako se to rješava kada imam intervala,pa ako mi netko može pojasnit malo.
Hvala
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
ajaxcy
Forumaš(ica)


Pridružen/a: 27. 09. 2009. (17:58:37)
Postovi: (77)16
Spol: 
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
|
| [Vrh] |
|
some_dude
Forumaš(ica)
Pridružen/a: 08. 11. 2009. (16:23:13)
Postovi: (59)16
Spol: 
Lokacija: Zd-Zg
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
|
| [Vrh] |
|
|










