zadatak s prošlogodišnjeg kolokvija em1 (zadatak)

[ante c]

neka su (0),(1).......(n-1) klase ostataka modulo n. dokazati da su svi ti skupovi međusobno različiti............muči me ovaj zad pa ako neko može pomoći
HVALA
p.s koristio ( umjesto [ zagrada

[Luuka]

uzmi x iz jedne od tih klasa i pokaži da se ne može nalaziti u drugoj
S tim ekvivalentno je, da ako je x u dvije klase, onda je to ustvari jedna te ista klasa.

npr. neka je x iz [i], pokažimo da je iz [j] akko [i]=[j]

jer je x iz [i], to znači da je x = i+k*n za neki k iz Z.
pretpostavimo da je također, x iz [j], to znači da je x = j+ m*n za m iz Z.

iz svega toga dobijemo da je:
i = j + (m-k)*n.

(*) To znači da je i iz [j], dakle [i] = [j] jer je svejedno kojeg reprezentata klase uzmemo.

alternativno: neka je x iz [i], i x iz [j], 0⇐i,j⇐n-1. Tada je i==j.
sve isto do (*), a nakon toga:

i iz [j], dakle i==j jer smo predstavnike uzeli između 0 i (n-1).

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[maty321]

na koji nacin mogu dokazati ovo (Ac n B)c = A U Bc
mogu samo preko demorganovih pravila ili??

[ante c]

[maty321]

pa i ja sam pocela tako ali bilo je prejednostavno pa..

svejedno hvala..

[ante c]

hmmmmmm.......imam još jedan nejasan zadatak ... pa ak se nekom da nek pogleda pa i riješi ak mu nije težak

Ako su A i B podskupovi on N takvi da je {A,B} particija od N, mora li tada {P(A),P(B)} biti particija skupa P(N)?.....najgore je šta odgovor treba detaljno obrazložit

[Luuka]

Rekao bih da ne

N={1,2,3}.
A={1,2}, B={3}

P(N) = { 0, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3} }
P(A) = { 0, {1}, {2}, {1,2} }
P(B) = { 0, {3} }

P(A) U P(B) = { 0, {1}, {2}, {1,2} ,{3} } != P(N)
pa ne može bit particija

dobar argument bi mogao biti kardinalnost:
|P(N)| = 2^n, ako je |N|=n.
za A,B takvi da čine particiju od N vrijedi:
|A|=k, |B|=n-k, pa je
|P(A)|=2^k
|P(B)|=2^(n-k)

Kad bi P(A) i P(B) bila particija od P(N), onda bi 2^k + 2^(n-k) = 2^n što vrijedi samo za k=0, ali tada nemamo particiju. (i nek je n>2)

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[ante c]

za svaki realan broj x postoji imaginaran broj z takav da je Re(z)=x ako je |z|=sqrt(x^2+1)______(korijen iz x na kvadrat +jedan)
pitanje je da li je sud istinit ......i da to obrazlošim.....sam kojim dobrim argumentom .............

[Luuka]

zapisano simbolima:



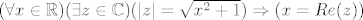
ja bih rekao da je implikacija istinita.

Implikacija P→Q je lažna samo ako je P istina, a Q laž.
Kod nas je P istina za z=(x,1) i z=(1,x), a Q je istina za z=(x,1).
Dakle, stvarno postoji takav z komplexan da mu je x realni dio

_________________
"Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy

[GoranV]

Kol. 08/09, 4. strana, 8. zadatak?? Unaprijed hvala

[gramzon]

Evo nesto mi nije jasno kod negacije.

Za svaki realan broj x vrijedi: ako je x2 veci od 5, onda je x veci od 10.

Negacija te izjave bi bila

Postoji realan broj x za koji vrijedi: ako je x manji ili jednak 10 x2 je veci od 5
?

[pbakic]

@goran:
ocito da tako zadana relacija nije refleksivna (jer |x-x|=0<1, dakle nijedan clan skupa ne moze biti u relaciji sam sa sobom), pa zato ne moze biti ni uredjaj, ni relacija ekvivalencije.
Simetricnost vrijedi jer je |x-y|=|y-x| za svaki izbor x,y (pa cim imas |x-y|>1 onda je ocito i |y-x|>1
Antisim ne vrijedi iz istog razloga zapravo, protuprimjer: |1-3|=|3-1|>1, a 1 i 3 su razliciti...
i tranzitivnost isto protuprimjer: |5-2|>1, |2-4|>1, ali onda bi trebalo biti |5-4|>1, sto nije...

@gramzon:
negacija je: postoji x takav da je x^2>5 i x<=10

[plonker]

[winks]

heeeelp...,
ok, nekoliko zadataka, ,
(1) ako su AnB=(prazan skup), mora li vrijediti (AnC)uB=(AuB)nC? svoj odgovor obrazložite.
ja mislim da ne vrijedi al imam malih problema oko dokazivanja.

(2) dan je sud: "za svaki prirodan broj m postoji realan broj x takav da ako je x*m=1, onda je x racionalan broj."
mislim da je istinito, al nisam sigurna. uzela sam kao primjer m=2, i x=1/2. jel to ok?

(3) koristeći matematičku indukciju dokažite da je 6^(2*2008) + 19^2008 +2^2009 djeljivo sa 17
i sad sam ja napisala da je k=2008, pa dobijem 6^2k + 19^k + 2^k+1; pa sam uvrstila da mi je k=1 al ne dobijem baš da je rezultat dijeljiv s 17, , nisam sigurna ni da je to ok kaj sam napravila...

(4) matematičkom indukcijom dokažite da za sve prirodne brojeve n vrijedi 4^n>n^2
za n=1 vrijedi, i sad napišem 4^(n+1)>(n+1)^2, raspišem ovo s desne strane kao kvadrat binoma, jel mogu ovo s lijeve strane rastaviti na 4^k * 4, a dalje zablokiram...,
zadnji, obećajem
(5) neka je S skup te neka su F i G particije skupa S sa sljedećim svojstvima:
-za svaki AeF postoji BeG takav da je A(podskup)B
-za svaki BeG postoji AeF takav da je B(podskup)A
mora li tada vrijediti F=G? svoj odgovor obrazložite.
{e-element, }

hvala...,

_________________
opusti se...,
najbolje stvari događaju se kad ih najmanje očekuješ..., =)),

[GoranV]

pbakic, hvala.

Al muci me ova simetričnost. Kaj je sa npr. x=2 i y=1 ? Kaj njih ne uzimam u obzir? Taj dio mi bas ne leži kak spada.

[ante c]

[pbakic]

pa zapravo i ne uzimas, jer simetricnost znaci samo da mora vrijediti implikacija:

xRy => yRx (ovdje R znaci "u relaciji s")
dakle imas uvjet samo kad vrijedi xRy, a kad x i y nisu u relaciji, nikom nista...

konkretno na primjeru x=2, y=1
x i y nisu u relaciji (jer ne vrijedi |2-1|>1), pa onda to nije protuprimjer ovoj implikaciji gore.

[Swerz]

[plonker]

@mlada pmf-ovka

(3) zamijeniš n sa 2008 i dobiješ...
6^2n+19^n+2^(n+1) što je po pretpostavci djeljivo sa 17...

Za n+1 ti to ovako izgleda:
6^2(n+1)+19^(n+1)+2^(n+2)=36*6^2n+19*19^n+2*2^(n+1)=...
izvučeš 36 van i namjestiš zagradu na pretopstavku a van zagrade oduzmeš ono što si dodala sa ovim namještanjem zagrade...
i dobiješ nešto ovako...
...=36*(6^2n+19^n+2^(n+1))-17*19^n-2*17*2^n=
=17(36*(6^2n+19^n+2^(n+1))-19^n-2*2^n)



(4)radili smo dosta takvih na vježbama...

za bazu 1 očito vrijedi...
napišeš 4^(n+1)=4*4^n>4*n^2
i sada moraš pokazati da je 4*n^2>=(n+1)^2
tj. rješiš tu kvadratnu nejednadžbu...tebe zanima kakve vrijednosti ta kvadratna nejednadžba poprima za n>=1...
ako je >=0 za sve n>=1 onda vrijedi 4*n^2>=(n+1)^2,a dalje očito i
4^(n+1)=4*4^n>4*n^2 tj. dokazali si da za sve prirodne brojeve n vrijedi 4^n>n^2 za n=1 vrijedi...

.

ispravite me ako sam neš fulao...

[Black Mamba]