| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
 Postano: 11:29 čet, 5. 11. 2009 Naslov: Postano: 11:29 čet, 5. 11. 2009 Naslov: |
    |
|
|
Moze mi netko rjesit ovaj zadatak, pliz:
Ako su A i B podskupovi od N takvi da je {A,B} particija od N, mora li tada {P(A),P(B)} biti particija skupa P(N)? Treba obrazlozt odgovor, naravno.. :)
Moze mi netko rjesit ovaj zadatak, pliz:
Ako su A i B podskupovi od N takvi da je {A,B} particija od N, mora li tada {P(A),P(B)} biti particija skupa P(N)? Treba obrazlozt odgovor, naravno.. 
|
|
| [Vrh] |
|
gramzon
Forumaš(ica)

Pridružen/a: 09. 07. 2009. (20:11:44)
Postovi: (3B)16
Spol: 
|
 Postano: 12:29 čet, 5. 11. 2009 Naslov: Postano: 12:29 čet, 5. 11. 2009 Naslov: |
    |
|
|
Imam problema s par zadataka a nisam bio u mogucnosti doci na konzultacije danas pa ako moze neko rijesiti ili dati hint
1. Neka su A,B i C podskupovi nekog univerzalnog skupa U. Vrijedi li sljedeća tvrdnja: "Ako je A [latex]\subseteq[/latex] B i B [latex]\bigcap[/latex] C [latex]\subseteq[/latex] A, onda je [latex]C^c[/latex] [latex]\bigcap[/latex] A [latex]\subseteq[/latex] [latex]B^c[/latex]"? Svoj odgovor potkrijepite dokazom ili kontraprimjerom.
(i sta je ovo [latex]C^c[/latex] i [latex]B^c[/latex] izgleda da nisam bio na tom predavanju)
2. Dokaži da je broj [latex]12^{n+2} + 13^{2n+1}[/latex] djeljiv sa 157 za svaki n [latex]\geq[/latex] 0
3. Napišite obrat i obrat po kontrapoziciji implikacije: [latex](\forall x \in R) : x \geq 5 \rightarrow x^2 \geq 25[/latex]
4. Napišite relaciju ekvivalencije na skupu S = {0,1,2,3,4,5,6,7} čije su klase [latex]k_0[/latex]={0,5}, [latex]k_1[/latex]={1,6}, [latex]k_2[/latex]={2,7}, [latex]k_3[/latex]={3}, [latex]k_4[/latex]={4}. Kako biste proširili ovu relaciju do relacije ekvivalencije na [latex]N \bigcup[/latex] {0} ?
I još nešto.
Koja svojstva ima slljedeća relacija na skupu S={1,2,3,4}:
{(1,2);(1,3);(1,4);(2,3);(2,4);(3,4)}
Ona je anstisimetrična i tranzitivna ?
Imam problema s par zadataka a nisam bio u mogucnosti doci na konzultacije danas pa ako moze neko rijesiti ili dati hint
1. Neka su A,B i C podskupovi nekog univerzalnog skupa U. Vrijedi li sljedeća tvrdnja: "Ako je A  B i B B i B  C C  A, onda je A, onda je 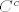  A A  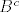 "? Svoj odgovor potkrijepite dokazom ili kontraprimjerom. "? Svoj odgovor potkrijepite dokazom ili kontraprimjerom.
(i sta je ovo 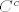 i i 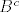 izgleda da nisam bio na tom predavanju) izgleda da nisam bio na tom predavanju)
2. Dokaži da je broj  djeljiv sa 157 za svaki n djeljiv sa 157 za svaki n 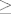 0 0
3. Napišite obrat i obrat po kontrapoziciji implikacije: 
4. Napišite relaciju ekvivalencije na skupu S = {0,1,2,3,4,5,6,7} čije su klase 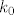 ={0,5}, ={0,5}, 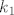 ={1,6}, ={1,6}, 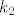 ={2,7}, ={2,7}, 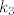 ={3}, ={3}, 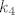 ={4}. Kako biste proširili ovu relaciju do relacije ekvivalencije na ={4}. Kako biste proširili ovu relaciju do relacije ekvivalencije na 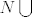 {0} ? {0} ?
I još nešto.
Koja svojstva ima slljedeća relacija na skupu S={1,2,3,4}:
{(1,2);(1,3);(1,4);(2,3);(2,4);(3,4)}
Ona je anstisimetrična i tranzitivna ?
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 14:05 čet, 5. 11. 2009 Naslov: Postano: 14:05 čet, 5. 11. 2009 Naslov: |
    |
|
|
[quote="miam"]Moze mi netko rjesit ovaj zadatak, pliz:
Ako su A i B podskupovi od N takvi da je {A,B} particija od N, mora li tada {P(A),P(B)} biti particija skupa P(N)? Treba obrazlozt odgovor, naravno.. :)[/quote]
cini se da ne mora, jer da bi neki skup (u ovom slucaju {P(A), P(B)}) bio particija, mora zadovoljavat ona 3 uvjeta:
1) presjek clanova je prazan skup:
presjek skupova P(A) i P(B) je ocito prazan, jer kad bi postojao neki skup S koji je istovremeno clan P(A) i P(B), onda bi bilo [latex] S \in A[/latex] i [latex]S \in B [/latex]
dakle S bi bio podskup od A i od B, pa bi presjek A i B bio neprazan =>
kontradikcija (s pretpostavkom da je {A,B} particija)
2) clanovi su neprazni skupovi (to se odmah vidi, jer su A i B neprazni)
3) unija clanova particije daje cijeli skup
ovaj uvjet nije (opcenito) zadovoljen, jer npr. skup [latex]A \cup B [/latex] nije u [latex]P(A) \cup P(B)[/latex], a ocito se nalazi u [latex]P(A \cup B) = P(N)[/latex]
za 3. mozes i nac konkretniji protuprimjer, mozda je i lakse, ak uzmes npr N={1,2},
A={1}, B={2}. Onda je [latex]P(A) \cup P(B)[/latex] {{1},{2}}, a [latex]P(A \cup B)[/latex] {{1},{2},{1,2}}
posto na 3. uvjetu pada, ovaj skup ne mora uvijek bit particija
| miam (napisa): | Moze mi netko rjesit ovaj zadatak, pliz:
Ako su A i B podskupovi od N takvi da je {A,B} particija od N, mora li tada {P(A),P(B)} biti particija skupa P(N)? Treba obrazlozt odgovor, naravno..  |
cini se da ne mora, jer da bi neki skup (u ovom slucaju {P(A), P(B)}) bio particija, mora zadovoljavat ona 3 uvjeta:
1) presjek clanova je prazan skup:
presjek skupova P(A) i P(B) je ocito prazan, jer kad bi postojao neki skup S koji je istovremeno clan P(A) i P(B), onda bi bilo 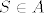 i i 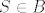
dakle S bi bio podskup od A i od B, pa bi presjek A i B bio neprazan ⇒
kontradikcija (s pretpostavkom da je {A,B} particija)
2) clanovi su neprazni skupovi (to se odmah vidi, jer su A i B neprazni)
3) unija clanova particije daje cijeli skup
ovaj uvjet nije (opcenito) zadovoljen, jer npr. skup 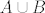 nije u nije u 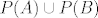 , a ocito se nalazi u , a ocito se nalazi u 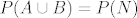
za 3. mozes i nac konkretniji protuprimjer, mozda je i lakse, ak uzmes npr N={1,2},
A={1}, B={2}. Onda je 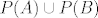 {{1},{2}}, a {{1},{2}}, a 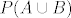 {{1},{2},{1,2}} {{1},{2},{1,2}}
posto na 3. uvjetu pada, ovaj skup ne mora uvijek bit particija
|
|
| [Vrh] |
|
niveus
Forumaš(ica)

Pridružen/a: 26. 10. 2009. (16:12:58)
Postovi: (5E)16
|
|
| [Vrh] |
|
Luuka
Forumaš(ica)


Pridružen/a: 13. 02. 2007. (20:34:54)
Postovi: (925)16
Spol: 
Lokacija: Hakuna Matata
|
 Postano: 15:27 čet, 5. 11. 2009 Naslov: Postano: 15:27 čet, 5. 11. 2009 Naslov: |
    |
|
|
potraži po forumu, već sam odgovorio na to. I zadatak nema baš smisla ako je unija na kraju, kad je presjek odgovor nije pretrivijalan.
[url]http://degiorgi.math.hr/forum/viewtopic.php?p=125280&highlight=#125280[/url]
potraži po forumu, već sam odgovorio na to. I zadatak nema baš smisla ako je unija na kraju, kad je presjek odgovor nije pretrivijalan.
http://degiorgi.math.hr/forum/viewtopic.php?p=125280&highlight=#125280
_________________ "Bolje bi prolazio na faxu da sam na drogama nego na netu" - by a friend of mine
"Poslije spavanja doma spavanje bilo di mi je najdraža stvar" - by the same guy  |
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
maty321
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (15:02:33)
Postovi: (7D)16
|
|
| [Vrh] |
|
miam
Forumaš(ica)

Pridružen/a: 03. 11. 2009. (11:19:45)
Postovi: (70)16
Spol: 
|
 Postano: 20:02 čet, 5. 11. 2009 Naslov: Postano: 20:02 čet, 5. 11. 2009 Naslov: |
    |
|
|
imam jedno pitanje, u onom zadatku sto sam pitala vec (na pocetku stranice ove), jel ne bi trebalo bit da je u P(AUB) i prazan skup?jer, za partitivni skup po definiciji, vrijedi da je to skup svih podskupa, pa onda i prazan skup ulazi u to..?mislim, ovo nije sad toliko bitno za taj zadatak, samo pitam opcenito..
imam jedno pitanje, u onom zadatku sto sam pitala vec (na pocetku stranice ove), jel ne bi trebalo bit da je u P(AUB) i prazan skup?jer, za partitivni skup po definiciji, vrijedi da je to skup svih podskupa, pa onda i prazan skup ulazi u to..?mislim, ovo nije sad toliko bitno za taj zadatak, samo pitam opcenito..
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
|










