| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 19:52 pon, 2. 11. 2009 Naslov: Postano: 19:52 pon, 2. 11. 2009 Naslov: |
    |
|
|
pretpostavimo da f postoji:
tada mora vrijediti [latex]f^{-1}(x^3) \leq f(f(x)^2 + f(x))[/latex]
djelujes opet s [latex]f^-1[/latex] (kako je ona padajuca, mijenja se predznak):
[latex]((f^{-1})^{-1})(x^3) \geq f(x)^2 + f(x)[/latex]
sad gledamo desnu stranu: za svaki f(x), mora vrijediti
[latex]f(x)^{2} + f(x) \geq -1/4[/latex] za svaki x (*)
(zato jer je -1/4 y koordinata tjemena kvadratne funkcije x^2 +x)
Time smo dobili da je desna strana veca od -1/4, promotrimo sada lijevu:
x^3 je surjekcija, i [latex]f^{-1}[/latex] je surjekcija (ocito, jer [latex]f^{-1}[/latex] mora biti bijekcija)
dakle na lijevoj strani imas kompoziciju 3 surjekcije, sto je opet surjekcija.
[latex]((f^{-1})^{-1})(x^3)[/latex] je surjekcija na R, pa ce sigurno postojati x takav da je
[latex]((f^{-1})^{-1})(x^3)[/latex] < -1/4, a to je kontradikcija sa (*), to jest cinjenicom da mora biti [latex]((f^{-1})^{-1})(x^3) \geq f(x)^2 + f(x) \geq -1/4[/latex]
pa takva funkcija ne postoji
pretpostavimo da f postoji:
tada mora vrijediti 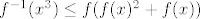
djelujes opet s  (kako je ona padajuca, mijenja se predznak): (kako je ona padajuca, mijenja se predznak):
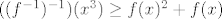
sad gledamo desnu stranu: za svaki f(x), mora vrijediti
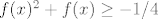 za svaki x (*) za svaki x (*)
(zato jer je -1/4 y koordinata tjemena kvadratne funkcije x^2 +x)
Time smo dobili da je desna strana veca od -1/4, promotrimo sada lijevu:
x^3 je surjekcija, i 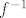 je surjekcija (ocito, jer je surjekcija (ocito, jer 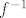 mora biti bijekcija) mora biti bijekcija)
dakle na lijevoj strani imas kompoziciju 3 surjekcije, sto je opet surjekcija.
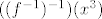 je surjekcija na R, pa ce sigurno postojati x takav da je je surjekcija na R, pa ce sigurno postojati x takav da je
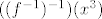 < -1/4, a to je kontradikcija sa (*), to jest cinjenicom da mora biti < -1/4, a to je kontradikcija sa (*), to jest cinjenicom da mora biti 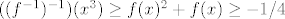
pa takva funkcija ne postoji
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 21:15 pon, 2. 11. 2009 Naslov: Postano: 21:15 pon, 2. 11. 2009 Naslov: |
    |
|
|
Pretpostavimo da postoji takva funkcija. Tada je [latex]f\circ f[/latex] rastuca kao kompozicija dviju padajucih f-ja. [latex]-f(x^3)[/latex] mozemo napisati kao kompoziciju [latex]g_1\circ f\circ g_2[/latex] pri cemu je [latex]g_1(x)=-x, g_2(x)=x^3[/latex], pa je [latex]g_1\circ f\circ g_2[/latex] strogo rastuca kao kompozicija strogo padajuce, padajuce i strogo rastuce f-je. Neka je [latex]h(x)=(f\circ f)(x)+(g_1\circ f\circ g_2)(x)[/latex]. [latex]h[/latex] je ocito strogo rastuca f-ja. S desne strane imamo funkciju [latex]2^f[/latex] koja je strogo padajuca kao kompozicija strogo rastuce i padajuce funkcije. Kako s lijeve strane jednakosti dobivamo strogo rastucu, a s desne strogo padajucu funkciju, dolazimo do kontradikcije. Dakle, ne postoji takav [latex]f[/latex].
Pretpostavimo da postoji takva funkcija. Tada je 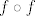 rastuca kao kompozicija dviju padajucih f-ja. rastuca kao kompozicija dviju padajucih f-ja. 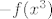 mozemo napisati kao kompoziciju mozemo napisati kao kompoziciju 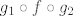 pri cemu je pri cemu je 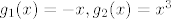 , pa je , pa je 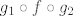 strogo rastuca kao kompozicija strogo padajuce, padajuce i strogo rastuce f-je. Neka je strogo rastuca kao kompozicija strogo padajuce, padajuce i strogo rastuce f-je. Neka je 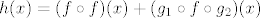 . . 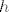 je ocito strogo rastuca f-ja. S desne strane imamo funkciju je ocito strogo rastuca f-ja. S desne strane imamo funkciju 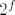 koja je strogo padajuca kao kompozicija strogo rastuce i padajuce funkcije. Kako s lijeve strane jednakosti dobivamo strogo rastucu, a s desne strogo padajucu funkciju, dolazimo do kontradikcije. Dakle, ne postoji takav koja je strogo padajuca kao kompozicija strogo rastuce i padajuce funkcije. Kako s lijeve strane jednakosti dobivamo strogo rastucu, a s desne strogo padajucu funkciju, dolazimo do kontradikcije. Dakle, ne postoji takav  . .
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 21:42 pon, 2. 11. 2009 Naslov: Postano: 21:42 pon, 2. 11. 2009 Naslov: |
    |
|
|
bilo bi lijepo da je tak, al nazalost, nitko ne kaze nadji f [b]strogo[/b] padajucu. Takodjer (opcenito), kompozicija [latex]f \circ g [/latex] gdje je f strogo rastuca a g samo rastuca ne mora bit [b]strogo[/b] rastuca (dakle dalje u zadatku ne mozes nista [b]strogo[/b] govorit o ovim kompozicijama)
@flame, ja sam isao rjesavat isto kao ti, ali kad dobijes
rastuca = padajuca, ne mozes rec da je to kontradikcija, jer moze biti
rastuca = padajuca ako je to konstanta (koja je istovremeno rastuca i padajuca, ocito)... kad se to dobije, zadatak se pocne jako komplicirat, i uopce nisam siguran da su ga zadali kako su htjeli...
ak tako krenes rjesavat, dobijes f(f(x)) = c za svaki x (c je konstanta)
takodjer, mora bit [latex]f(x^{3}) + 2^{f(x)} = c [/latex]
Preglednosti radi, napravimo supstituciju, [latex]t=x^{3}.[/latex]
Sad imamo: [latex]f(t) + 2^{f(\sqrt[3]{t})} =c[/latex]
ili bolje: [latex]f(t) = c - 2^{f(\sqrt[3]{t})}[/latex].
Uocimo, f je padajuca, treci korijen rastuca, pa je [latex]c - 2^{f(\sqrt[3]{t})}[/latex] rastuca (*)
* vrijedi jer je 3. korijen rastuca, f(treci korijen) onda ocito padajuca, 2 na to cudo takodjer padajuca, i to sve sa minus predznakom rastuca.
s tim opet imamo jednakost padajuce [latex](f(t))[/latex] i rastuce [latex]c - 2^{f(\sqrt[3]{t})}[/latex], istom argumentacijom dobivamo da su obje strane konstante => f(t) je konstanta, a posto t=x^3 prolazi kroz cijeli R,
mora biti f(x) je konstanta.
Dalje je lagano, jer imas iz pocetnog uvjeta:
[latex]c - c = 2^{c} => 0= 2^c[/latex] , sto je ocita kontradikcija
Naravno, ovaj zadnji korak (poslije *) je naknadna pamet, o tom nisam bas stigo razmislit tak posteno unutar onog vremena na kolokvij...
bilo bi lijepo da je tak, al nazalost, nitko ne kaze nadji f strogo padajucu. Takodjer (opcenito), kompozicija 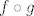 gdje je f strogo rastuca a g samo rastuca ne mora bit strogo rastuca (dakle dalje u zadatku ne mozes nista strogo govorit o ovim kompozicijama) gdje je f strogo rastuca a g samo rastuca ne mora bit strogo rastuca (dakle dalje u zadatku ne mozes nista strogo govorit o ovim kompozicijama)
@flame, ja sam isao rjesavat isto kao ti, ali kad dobijes
rastuca = padajuca, ne mozes rec da je to kontradikcija, jer moze biti
rastuca = padajuca ako je to konstanta (koja je istovremeno rastuca i padajuca, ocito)... kad se to dobije, zadatak se pocne jako komplicirat, i uopce nisam siguran da su ga zadali kako su htjeli...
ak tako krenes rjesavat, dobijes f(f(x)) = c za svaki x (c je konstanta)
takodjer, mora bit 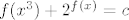
Preglednosti radi, napravimo supstituciju, 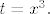
Sad imamo: 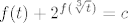
ili bolje: 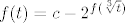 . .
Uocimo, f je padajuca, treci korijen rastuca, pa je 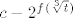 rastuca (*) rastuca (*)
* vrijedi jer je 3. korijen rastuca, f(treci korijen) onda ocito padajuca, 2 na to cudo takodjer padajuca, i to sve sa minus predznakom rastuca.
s tim opet imamo jednakost padajuce 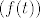 i rastuce i rastuce 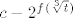 , istom argumentacijom dobivamo da su obje strane konstante ⇒ f(t) je konstanta, a posto t=x^3 prolazi kroz cijeli R, , istom argumentacijom dobivamo da su obje strane konstante ⇒ f(t) je konstanta, a posto t=x^3 prolazi kroz cijeli R,
mora biti f(x) je konstanta.
Dalje je lagano, jer imas iz pocetnog uvjeta:
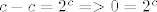 , sto je ocita kontradikcija , sto je ocita kontradikcija
Naravno, ovaj zadnji korak (poslije *) je naknadna pamet, o tom nisam bas stigo razmislit tak posteno unutar onog vremena na kolokvij...
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
tmarusca
Forumaš(ica)


Pridružen/a: 28. 06. 2009. (20:53:52)
Postovi: (59)16
Spol: 
Lokacija: 1/039
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 22:32 čet, 5. 11. 2009 Naslov: Postano: 22:32 čet, 5. 11. 2009 Naslov: |
    |
|
|
Umoljen sam prenijeti sljedece rjesenje:
Postoji li padajuca funkcija [latex]f: \mathbb{R} \to \mathbb{R}[/latex] takva da vrijedi
[latex]f(f(x))-f(x^3)=2^{f(x)}[/latex], za sve [latex]x \in \mathbb{R}[/latex]?
Pretpostavimo da takva [latex]f[/latex] postoji. Tada je [latex]f(f(x))-2^{f(x)}=f(x^3)[/latex], za sve [latex]x \in \mathbb{R}[/latex].
Definirajmo funkcije [latex]g,h: \mathbb{R} \to \mathbb{R}[/latex] s
[latex]g(x):=f(f(x))-2^{f(x)}[/latex] i
[latex]h(x):=f(x^3)[/latex].
Tada je [latex]g[/latex] rastuca, a [latex]h[/latex] padajuca, pa je nuzno
[latex]g=h[/latex] konstantna funkcija.
Dakle, postoji [latex]c \in \mathbb{R}[/latex] takav da je [latex]h(x)=f(x^3)=c[/latex], za sve [latex]x \in \mathbb{R}[/latex]. No, tada je i [latex]f(x)=c[/latex], za sve [latex]x \in \mathbb{R}[/latex]. Ako to uvrstimo u pocetnu funkcijsku jednadzbu, dobivamo
[latex]0=c-c=2^{c}[/latex]; kontradikcija.
Umoljen sam prenijeti sljedece rjesenje:
Postoji li padajuca funkcija 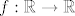 takva da vrijedi takva da vrijedi
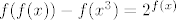 , za sve , za sve 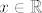 ? ?
Pretpostavimo da takva  postoji. Tada je postoji. Tada je 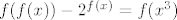 , za sve , za sve 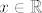 . .
Definirajmo funkcije 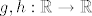 s s
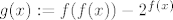 i i
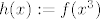 . .
Tada je  rastuca, a rastuca, a 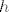 padajuca, pa je nuzno padajuca, pa je nuzno
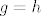 konstantna funkcija. konstantna funkcija.
Dakle, postoji 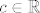 takav da je takav da je 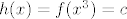 , za sve , za sve 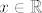 . No, tada je i . No, tada je i 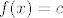 , za sve , za sve 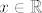 . Ako to uvrstimo u pocetnu funkcijsku jednadzbu, dobivamo . Ako to uvrstimo u pocetnu funkcijsku jednadzbu, dobivamo
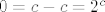 ; kontradikcija. ; kontradikcija.
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
 Postano: 16:16 sub, 23. 10. 2010 Naslov: Postano: 16:16 sub, 23. 10. 2010 Naslov: |
    |
|
|
[quote="pbakic"]pretpostavimo da f postoji:
tada mora vrijediti [latex]f^{-1}(x^3) \leq f(f(x)^2 + f(x))[/latex]
djelujes opet s [latex]f^-1[/latex] (kako je ona padajuca, mijenja se predznak):
[latex]((f^{-1})^{-1})(x^3) \geq f(x)^2 + f(x)[/latex]
sad gledamo desnu stranu: za svaki f(x), mora vrijediti
[latex]f(x)^{2} + f(x) \geq -1/4[/latex] za svaki x (*)
(zato jer je -1/4 y koordinata tjemena kvadratne funkcije x^2 +x)
Time smo dobili da je desna strana veca od -1/4, promotrimo sada lijevu:
[color=red]x^3 je surjekcija, i [latex]f^{-1}[/latex] je surjekcija (ocito, jer [latex]f^{-1}[/latex] mora biti bijekcija)
dakle na lijevoj strani imas kompoziciju 3 surjekcije, sto je opet surjekcija.
[latex]((f^{-1})^{-1})(x^3)[/latex] je surjekcija na R, pa ce sigurno postojati x takav da je
[latex]((f^{-1})^{-1})(x^3)[/latex] < -1/4,[/color] a to je kontradikcija sa (*), to jest cinjenicom da mora biti [latex]((f^{-1})^{-1})(x^3) \geq f(x)^2 + f(x) \geq -1/4[/latex]
pa takva funkcija ne postoji[/quote]
Oke, sad meni stvarno nije jasno kako smo dobili ovaj dio da [color=red]postoji x t.d. je [/color][latex]((f^{-1}(x^3)<(-1/4)[/latex]. Kakooo?
| pbakic (napisa): | pretpostavimo da f postoji:
tada mora vrijediti 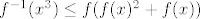
djelujes opet s  (kako je ona padajuca, mijenja se predznak): (kako je ona padajuca, mijenja se predznak):
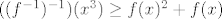
sad gledamo desnu stranu: za svaki f(x), mora vrijediti
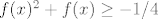 za svaki x (*) za svaki x (*)
(zato jer je -1/4 y koordinata tjemena kvadratne funkcije x^2 +x)
Time smo dobili da je desna strana veca od -1/4, promotrimo sada lijevu:
x^3 je surjekcija, i 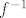 je surjekcija (ocito, jer je surjekcija (ocito, jer 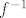 mora biti bijekcija) mora biti bijekcija)
dakle na lijevoj strani imas kompoziciju 3 surjekcije, sto je opet surjekcija.
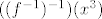 je surjekcija na R, pa ce sigurno postojati x takav da je je surjekcija na R, pa ce sigurno postojati x takav da je
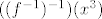 < -1/4, a to je kontradikcija sa (*), to jest cinjenicom da mora biti < -1/4, a to je kontradikcija sa (*), to jest cinjenicom da mora biti 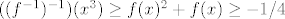
pa takva funkcija ne postoji |
Oke, sad meni stvarno nije jasno kako smo dobili ovaj dio da postoji x t.d. je 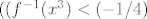 . Kakooo? . Kakooo?
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
|
| [Vrh] |
|
medonja
Forumaš(ica)


Pridružen/a: 20. 10. 2009. (17:01:04)
Postovi: (45)16
|
|
| [Vrh] |
|
|

















