| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
scenic
Forumaš(ica)

Pridružen/a: 06. 11. 2009. (18:27:51)
Postovi: (1)16
|
|
| [Vrh] |
|
piskalo
Forumaš(ica)


Pridružen/a: 27. 09. 2008. (21:33:53)
Postovi: (B)16
Spol: 
Lokacija: NP
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
allllice
Forumaš(ica)
Pridružen/a: 16. 09. 2005. (14:31:59)
Postovi: (121)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:51 pet, 6. 11. 2009 Naslov: Postano: 19:51 pet, 6. 11. 2009 Naslov: |
    |
|
|
Ako uzmem u obzir da se tu radi u biti o krugu, onda pretpostavljam da to ide ovako nekako:
Trazimo duzinu koja ce ciniti pola povrsine pocetnog kruga. Standardna povrsina kruga je
[latex]P=r^2*\Pi [/latex], i to lako izracunamo.
Nama treba povrsina polovice, [latex]P_{pola}=\frac{P}{2} [/latex], sto isto lako izracunamo.
I onda po formuli [latex]P_{pola}=r_{pola}^2*\Pi [/latex] dobijemo trazenu duzinu, [latex]r_{pola} [/latex]
Odnosno, krace:
[latex]\frac{r^2*\Pi}{2}=r_{pola}*\Pi [/latex] , iz cega se izracuna [latex]r_{pola} [/latex] , i to je to
Ako uzmem u obzir da se tu radi u biti o krugu, onda pretpostavljam da to ide ovako nekako:
Trazimo duzinu koja ce ciniti pola povrsine pocetnog kruga. Standardna povrsina kruga je
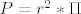 , i to lako izracunamo. , i to lako izracunamo.
Nama treba povrsina polovice, 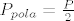 , sto isto lako izracunamo. , sto isto lako izracunamo.
I onda po formuli 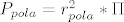 dobijemo trazenu duzinu, dobijemo trazenu duzinu, 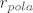
Odnosno, krace:
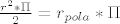 , iz cega se izracuna , iz cega se izracuna 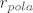 , i to je to , i to je to
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
allllice
Forumaš(ica)
Pridružen/a: 16. 09. 2005. (14:31:59)
Postovi: (121)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 0:59 sub, 7. 11. 2009 Naslov: Postano: 0:59 sub, 7. 11. 2009 Naslov: |
    |
|
|
ne da mi se crtati i raspisivati, ali napisat ću ideju:
koristit ću vsegine oznake iz trećeg posta. označimo još točku u kojoj je kravino uže privezano s T (središte od K2), i točke u kojima se sijeku kružnice (rubovi od K1 i K2) s A i B. površinu presjeka (P, za koju znamo da iznosi R^2*Pi/2) možemo promatrati kao zbroj tri površine: jednu površinu isječka kruga K2 s lukom AB (nazovimo ju P1), te dvije (jednake) površine odsječaka kruga K1 s duljinom "baze" (ne znam kako se to zove; uglavnom te "baze" su dužine AT i BT) upravo r (nazovimo svaku P2; jednake su). nacrtaj si sliku. e sad si lijepo pogledaš formule za površine kružnog isječka i odsječka. tu se spominju neki kutovi koje lako izraziš pomoću R i r. i onda iz pretpostavke da je površina presjeka K1 i K2 jednaka polovici površine K1 (dakle, P = P1 + 2*P2) izraziš r pomoću R.
nije teško, ali ima posla s računanjem. nadam se da je jasno što želim reći. ako ne bude, potrudit ću se uskoro bolje izreći ideju.
ne da mi se crtati i raspisivati, ali napisat ću ideju:
koristit ću vsegine oznake iz trećeg posta. označimo još točku u kojoj je kravino uže privezano s T (središte od K2), i točke u kojima se sijeku kružnice (rubovi od K1 i K2) s A i B. površinu presjeka (P, za koju znamo da iznosi R^2*Pi/2) možemo promatrati kao zbroj tri površine: jednu površinu isječka kruga K2 s lukom AB (nazovimo ju P1), te dvije (jednake) površine odsječaka kruga K1 s duljinom "baze" (ne znam kako se to zove; uglavnom te "baze" su dužine AT i BT) upravo r (nazovimo svaku P2; jednake su). nacrtaj si sliku. e sad si lijepo pogledaš formule za površine kružnog isječka i odsječka. tu se spominju neki kutovi koje lako izraziš pomoću R i r. i onda iz pretpostavke da je površina presjeka K1 i K2 jednaka polovici površine K1 (dakle, P = P1 + 2*P2) izraziš r pomoću R.
nije teško, ali ima posla s računanjem. nadam se da je jasno što želim reći. ako ne bude, potrudit ću se uskoro bolje izreći ideju.
_________________
ima let u finish
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ma
Forumaš(ica)


Pridružen/a: 27. 01. 2007. (12:06:50)
Postovi: (347)16
Spol: 
|
 Postano: 17:09 sub, 7. 11. 2009 Naslov: Postano: 17:09 sub, 7. 11. 2009 Naslov: |
    |
|
|
e zgodna sličica. iz nje same vidiš da se ne radi o dva kružna isječka (u protivnom bismo imali da su polumjeri oba kruga isti, što bi značilo da krava može doći samo do centra livade, a tada ne bi mogla pojesti pola livade, nego manje), nego o jednom isječku (P1) i dva odsječka (P2).
malo sam nadopunio skicu:
[img]http://img24.imageshack.us/img24/8189/matproblem.jpg[/img]
dakle, uz oznake kao na slici, imaš:
[latex]P_1 = \frac{r^2\pi\alpha}{360°}[/latex]
[latex]P_2 = \frac{R^2}{2}(\frac{\pi\beta}{180}-\sin\beta)[/latex]
(to je iz žutih tablica, kuteve uvrštavaš u stupnjevima)
gdje kuteve alfa i beta jednostavno dobiješ iz tih nekih trokutića sa slike. recimo:
[latex]\sin\frac{\beta}{2} = \frac{r}{2R}[/latex]
[latex]\cos\frac{\alpha}{2} = \frac{r}{2R}[/latex]
na kraju samo dobiveno uvrstiš u:
[latex]\frac{R^2\pi}{2} = P_1 + 2P_2[/latex]
dobit ćeš r izražen pomoću R, a to ti i treba. (R je polumjer livade, a r duljina užeta - i naravno: r>R)
sad jasno?
e zgodna sličica. iz nje same vidiš da se ne radi o dva kružna isječka (u protivnom bismo imali da su polumjeri oba kruga isti, što bi značilo da krava može doći samo do centra livade, a tada ne bi mogla pojesti pola livade, nego manje), nego o jednom isječku (P1) i dva odsječka (P2).
malo sam nadopunio skicu:

dakle, uz oznake kao na slici, imaš:
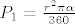
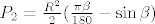
(to je iz žutih tablica, kuteve uvrštavaš u stupnjevima)
gdje kuteve alfa i beta jednostavno dobiješ iz tih nekih trokutića sa slike. recimo:
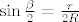
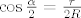
na kraju samo dobiveno uvrstiš u:
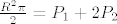
dobit ćeš r izražen pomoću R, a to ti i treba. (R je polumjer livade, a r duljina užeta - i naravno: r>R)
sad jasno?
_________________
ima let u finish
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
Crazylamb1
Forumaš(ica)


Pridružen/a: 09. 06. 2006. (01:17:33)
Postovi: (12E)16
Spol: 
Lokacija: Albertane, Mars
|
|
| [Vrh] |
|
Krava
Gost
|
|
| [Vrh] |
|
markooooooo
Gost
|
|
| [Vrh] |
|
|












